![]() , (4.1)
, (4.1)
где pн и rн – давление и плотность жидкости при нормальных условиях, c –скорость звука в жидкости. Плотность выражается через объем Vi и массу жидкостиmi:
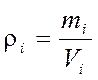 . (4.2)
. (4.2)
Изменение массы жидкости в рабочей камере V1:
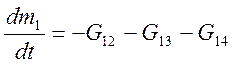 . (4.3)
. (4.3)
Здесь и ниже Gij – массовый расход из объема i в объем j. Объем V1 определяется из соотношения:
![]() . (4.4)
. (4.4)
Изменение массы и объем жидкости в основном аккумуляторе V2:
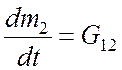 , (4.5)
, (4.5)
![]() . (4.6)
. (4.6)
Здесь Fi – площадь резинокордовой мембраны, а zмi – среднее смещение мембраны в i-м аккумуляторе. Уравнения для объемов 3 и 4 имеют вид:
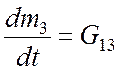 , (4.7)
, (4.7)
![]() , (4.8)
, (4.8)
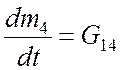 , (4.9)
, (4.9)
![]() . (4.10)
. (4.10)
Движение резинокордовых мембран в аккумуляторах 2, 3 и 4 условно приводится к точке, скорость которой равна осредненной по площади мембраны. Значение приведенной массы мембраны определяется по следующей формуле (получена по условию тождества кинетической энергии реальной мембраны и приведенной системы с одной степенью свободы):
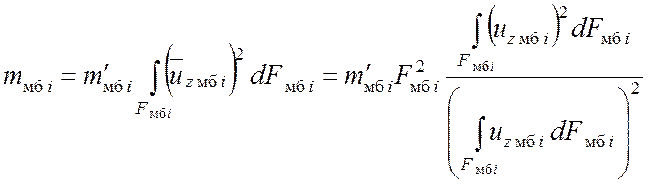 . (4.11)
. (4.11)
Здесь uzмбi – проекция скорости элемента dFмбi на нормаль к поверхности
мембраны, 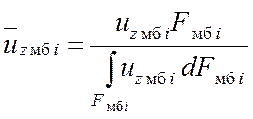 – отношение нормальной скорости
элемента к средней по площади.
– отношение нормальной скорости
элемента к средней по площади.
Уравнения динамики мембраны (точнее, ее характерной точки, скорость которой совпадает со средней по площади):
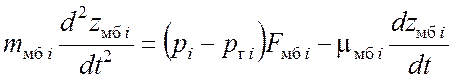 . (4.12)
. (4.12)
Здесь pгi – давление в газовой полости аккумулятора i, mмбi – приведенный коэффициент демпфирования. Поскольку мембрана приводится к точке со средней по площади нормальной скоростью, коэффициент приведения силы давления равен единице. В случае, если мембрана прижимается к перфорированной стенке, перемещение принимается равным предельному значению, которое определяется значением объема. Упругость мембраны считалась малой по сравнению с силой давления.
Изменение давления в газовых полостях дополнительных аккумуляторов давления (3 и 4) описывается уравнениями адиабаты (поскольку время воздействия мало, теплоотдачей в стенки можно пренебречь):
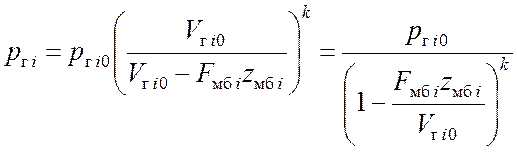 . (4.13)
. (4.13)
Здесь pгi0 и Vгi0 – начальное давление и начальный объем газовой полости i-го аккумулятора давления, k – коэффициент адиабаты.
Для газовых полостей второго аккумулятора и пневматического переливного клапана (присвоим параметрам в нем индекс 5) в качестве основных (интегрируемых) переменных будем рассматривать массу газа (m2, m5) и энергию газа (E2, E5). Поскольку начальная температура газа равнялась температуре стенок, а время нагружения амортизатора при воздействии УВ мало, в уравнении энергии будем пренебрегать теплоотдачей от газа в стенки.
Уравнение изменения массы газа в объеме V2г:
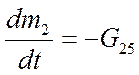 . (4.12)
. (4.12)
Уравнение изменения энергии газа в объеме V2г:
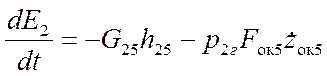 .
(4.13)
.
(4.13)
Уравнение изменения массы газа в объеме V5г:
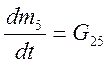 . (4.14)
. (4.14)
Уравнение изменения энергии газа в объеме V5г:
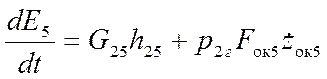 , (4.15)
, (4.15)
В данных уравнениях G25 – массовый
расход газа из объема V2г в объем V5г (при течении в обратном направлении G25<0), r25
и h25 – плотность и полная удельная
энтальпия газа, истекающего из объема в объем, 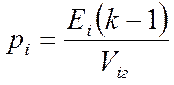 –
давление, k – коэффициент адиабаты.
–
давление, k – коэффициент адиабаты.
Значения объемов определяются по следующим соотношениям:
![]() , (4.16)
, (4.16)
![]() , (4.17)
, (4.17)
Далее рассмотрим методику расчета истечения из объема 1 в объем 2 и обратно, процесс истечения можно считать квазистационарным. Пусть, для определенности, p2>p5, т.е. газ течет из объема 2 в объем 5 (в противном случае в последующих выражениях следует заменить индекс «2» на «5» и «5» на «2», и учесть, что G25=-G52, uист 25=-uист 52 и h25=h52).
1. Определяем критическое давление в минимальном сечении (давление, соответствующее числу Маха М25=1):
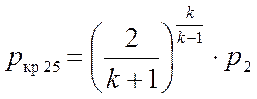 ;
;
2. Давление в вытеснительном объеме p2 сравнивается с критическим. Истинное значение давления в критическом сечении равно большему из двух:
p25= max(pкр25, p5). (4.18)
Режим течения при случае, если p5>pкр25 называется докритическим, а в противном случае – критическим. При критическом режиме течения число Маха в критическом (минимальном) сечении M25=1;
3. Определяем плотность газа в минимальном сечении:
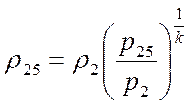 (4.19)
(4.19)
4. Определяем скорость газа в минимальном сечении:
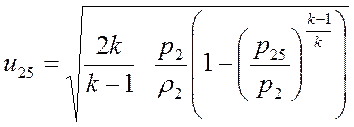 ; (4.20)
; (4.20)
5. Массовый расход газа через отверстие:
![]() . (4.21)
. (4.21)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.