Разработка амортизатора для защиты транспортно-пускового контейнера с изделием, находящимся в подвижной пусковой установке, от заданного внешнего воздействия, страница 7

Здесь p₀=p_2г0 – начальное давление в амортизаторе, 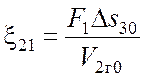, F₁ – площадь сечения рабочей камеры амортизатора V₁, k –показатель адиабаты. Используя эти соотношения, можно определить суммарное усилие пояса амортизации при Ds=Ds₃₀:

.

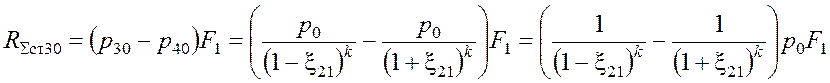Или, учитывая (3.3) и (3.5):

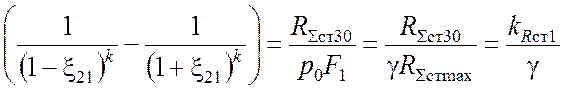.                              (3.10)

Из данного уравнения можно определить искомую величину x₂₁.

Рассмотрим дальнейшее сжатие амортизатора от Ds₃₀ до Ds_max. Изменение давления на этой стадии определяется адиабатическим сжатием газа в полостях  V_г2 и V_г3, которые работают как единая полость. Начальный (при Ds=Ds₃₀) объем этой полости: , где 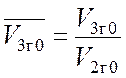 – отношение начальных объемов газа в основном и первом дополнительном аккумуляторах давления. Имеем:

.

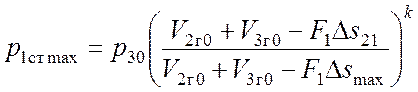Преобразуем данное равенство, учитывая (3.8):

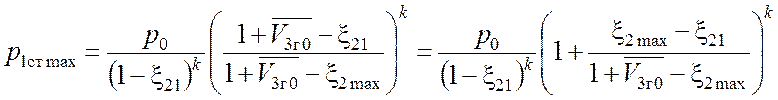(3.11)

Здесь 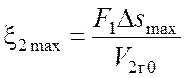. Заметим, что в отличие от , данная величина собычно больше единицы. Ее можно определить, используя (3.4):

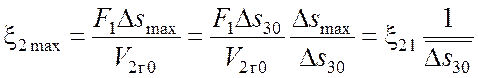.                                          (3.12)

Давление в рабочей камере полностью растянутого амортизатора (Ds=-Ds_max) определяется адиабатическим расширением газа в совместно работающих камерах V_г2 и V_г4 от объема  при Ds=-Ds₃₀ до , при Ds=-Ds_max где 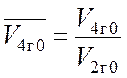. Имеем:

.

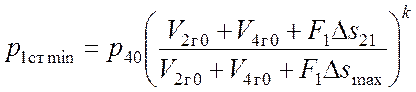Преобразуем данное равенство, учитывая (3.9):

.

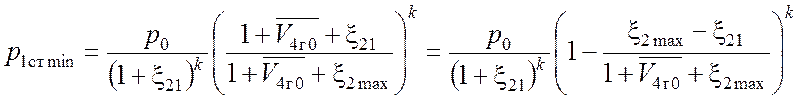Далее подставим (3.8), (3.9), (3.11) и последнее уравнение в (3.6):

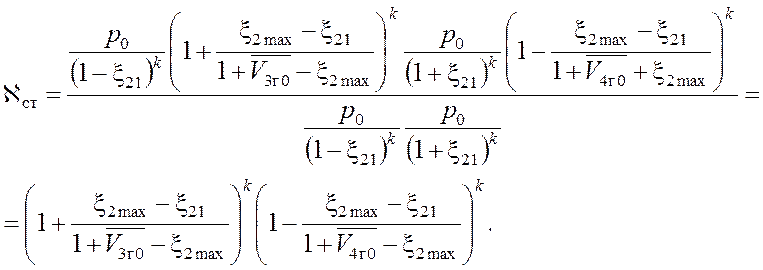(3.13)

С другой стороны, максимальное статическое усилие амортизатора можно выразить так:

.

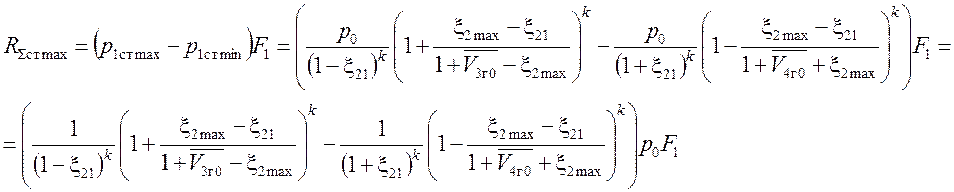          Используя (3.13) можно исключить из этого уравнения . Также учтем (3.3):

.                  

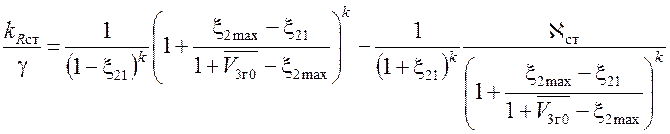Введем обозначение 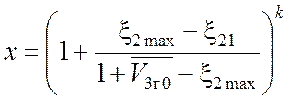. Имеем:

,

,

,

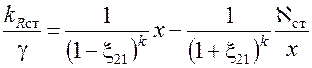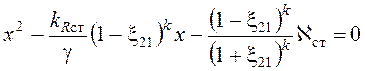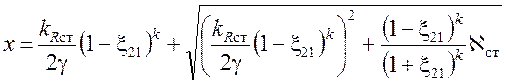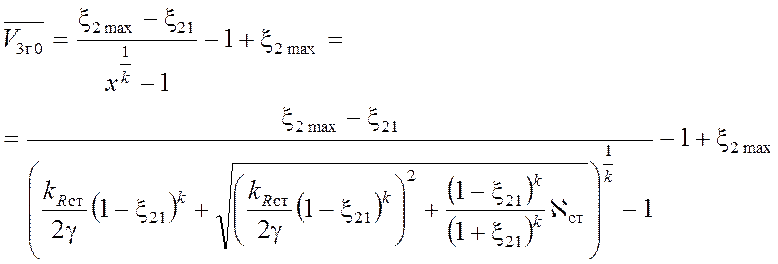(3.14)

Далее из уравнения (3.13) можно определить :

,

,

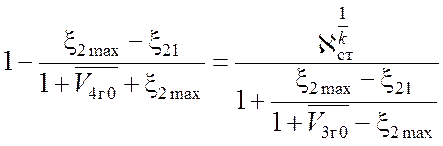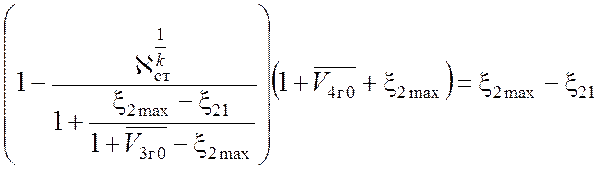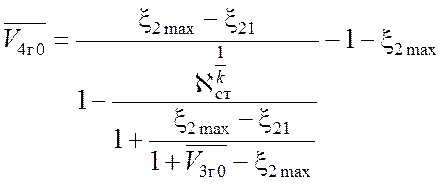 (3.15)
          Подставим (3.1) в (3.11):

.

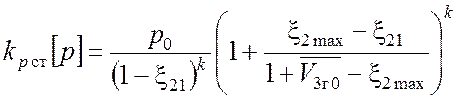Тогда

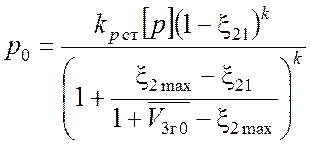.                                                                 (3.16)

Тогда площадь рабочей камеры вычисляется из (3.3):

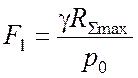.                                                                                           (3.17)

Диаметр рабочей камеры:

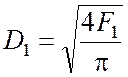.                                                                                            (3.18)

Начальные объемы газовых камер аккумуляторов:    

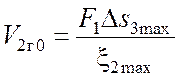,    , .                               (3.19)

Далее выберем сечения дросселей F_др3 и F_др4. Рассмотрим движение ТПК при обратном ходе. На ТПК действует упругая сила со стороны амортизаторов, значение которой при Ds=Ds₃₀:

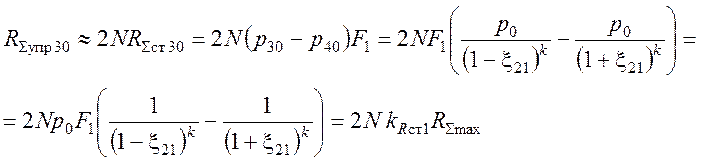.                   (3.20)

В этой формуле N – число поясов амортизаторов (по две пары амортизаторов, установленных навстречу друг другу в каждом).

Из (3.7) определяем расчетную скорость обратного хода:

 .                                             (3.21)

Демпфирующие усилия амортизаторов:

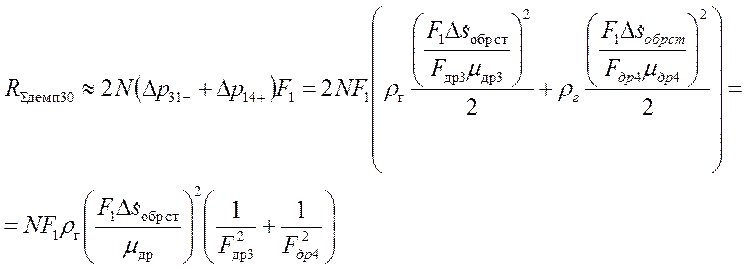      (3.22)

Здесь r_г – плотность жидкости,  – перепад давления между камерами V₃ и V₁ амортизатора, который на прямом ходе был сжат,  – перепад давления между камерами V₁ иV₄ амортизатора, который на прямом ходе был растянут, m_др3=m_др4=m_др – коэффициент расхода жидкости через дроссель.

Будем считать, что в момент, когда Ds=Ds₃₀, корпус ППУ уже перестал двигаться. Тогда в предположении, что движение ТПК – установившееся, можно приравнять (3.20) и (3.22):

,

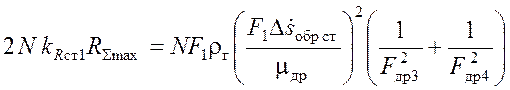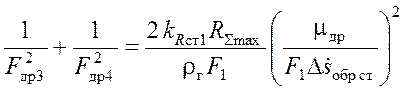.                                                     (3.23)

Таким образом, имеем одно условие для определения двух неизвестных: F_др3 и F_др4. Можно принять размеры дросселей (а значит и перепады давлений на них) одинаковыми, тогда:

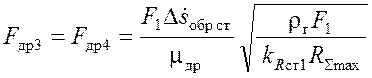.                                                         (3.24)

Другой подход предполагает учет ограничений по максимальному и минимальному давлениям в камерах V₁ сжимаемого и растягиваемого амортизаторов. Для амортизатора, который сжимался на прямом ходе и растягивается на обратном, должно выполняться условие:

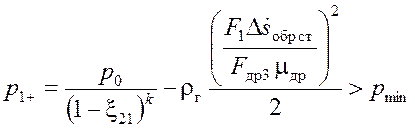.                                                   (3.25)₁

Для амортизатора, который растягивался на прямом ходе и сжимается на обратном, должно выполняться условие:

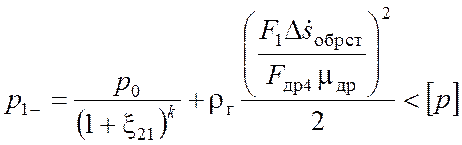.                                            (3.25)₂

Потребуем равенства отношений  и . Это условие по сути означает равный относительный запас по условиям (3.25) для обоих камер. Имеем:

          , 

,                       

.

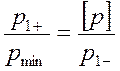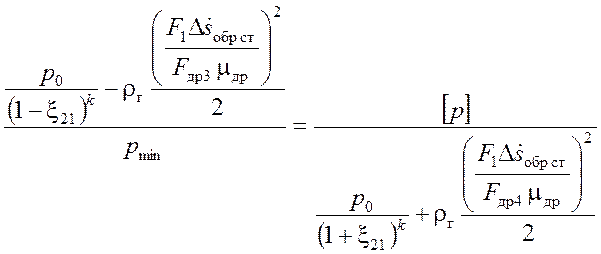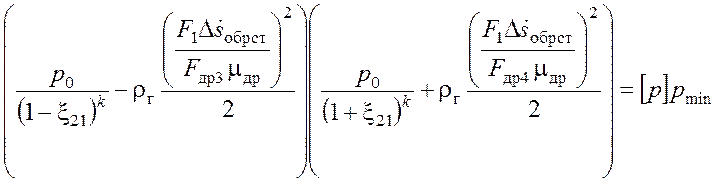Из (3.23) выразим F_др3 через F_др4 и подставим в данное уравнение:

,

,

.

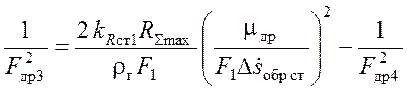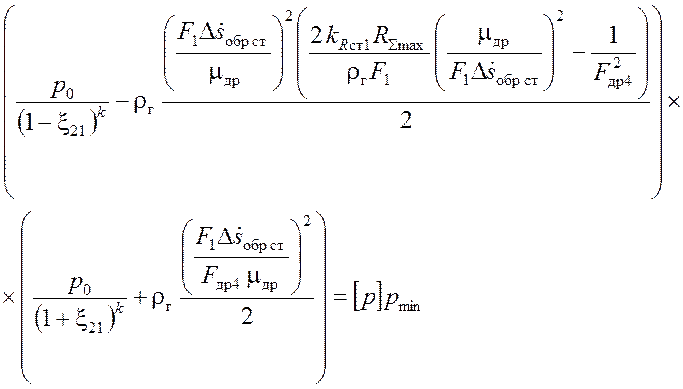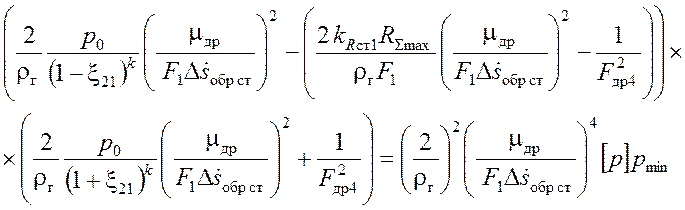Введем обозначения:

,

,

.

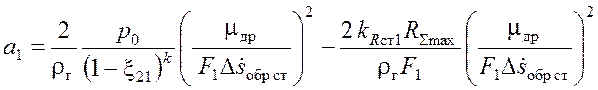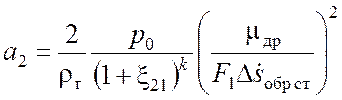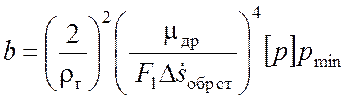Тогда уравнение перепишется в виде:

,         

,     

,               

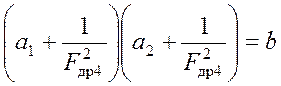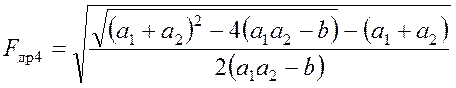.                                             (3.26)

и из (3.23):

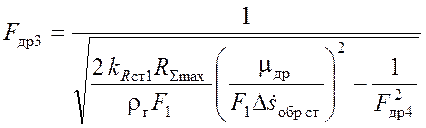.                                                (3.27)

Независимо от способа определения F_др3, F_др4 далее необходимо проверить выполнение условий (3.25)₁ и (3.25)₂ и при необходимости увеличить площадь соответствующего дросселя. В дальнейшем при проведении динамических расчетов следует проверить эти условия уже по расчетным значениям давлений и также при необходимости увеличить площади дросселей.

4. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ПНЕВМОГИДРАВЛИЧЕСКОГО АМОРТИЗАТОРА

Основной проблемой при численном моделировании работы пневмогидравлических амортизаторов является способ определения перепада давлений между гидравлическими полостями V₁, V₂, V₃ и V₄. На стадии прямого хода ТПК для правильно спроектированного амортизатора этим перепадом можно пренебречь, однако при этом возникает вопрос о том, относится ли схема с заданными параметрами к «правильно спроектированным», т.е. выполняется ли условие малости перепада в действительности? На стадии обратного хода учитывать этот перепад необходимо (он обеспечивает демпфирование), однако возникает вопрос о способе учета. Первый вариант, основанный на предположении о том, что клапан в каждый момент времени находится в состоянии равновесия, не позволяет оценить время закрытия клапана и установления течения через дроссель, т.е. проверить, возможен ли заброс давления и, если да, какова его величина. Желательно проводить расчет динамики клапана, однако при этом возникает проблема определения гидродинамических сил действующих на клапан. При малых (во много раз меньших, чем диаметр клапана) зазорах можно считать, что гидродинамическая сила мала по сравнению с гидростатической, но при дальнейшем открытии клапана это допущение становится некорректным. Наиболее точным является использование феноменологической модели течения жидкости через клапанную коробку. Относительным недостатком такого подхода является необходимость существенного уменьшения шага интегрирования, обусловленная требованиями устойчивости. Далее будем использовать именно такой подход. При этом, поскольку размеры камер сравнительно невелики, можно пренебречь переменностью параметров жидкости по длине камер, т.е. использовать нульмерную схему. Из уравнений, описывающих совместную динамику клапанов и истекающей жидкости, будем определять расходы жидкости из объема в объем, а также изменение объемов (при перемещениях клапанов). Для каждого из гидравлических объемов i=1..4 будем записывать уравнение изменения массы, полагая, что давление p_i однозначно выражается через плотность r_i: