Характеристика резерву несучої здатності гака:
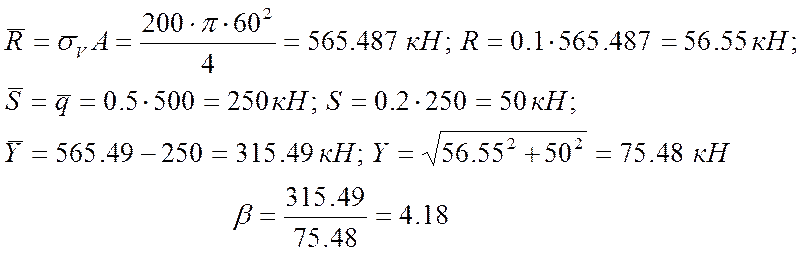
Імовірність відмови гака:
-
Ефективна частота випадкового процесу резерву несучої здатності ![]() :
:
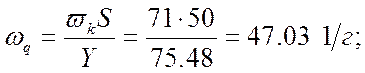
- Коефіцієнт широкополосності:
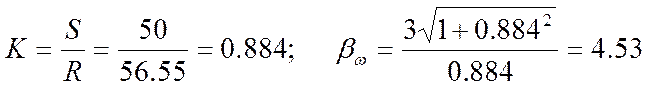
- Ймовірність відмови гака за наробіток t:
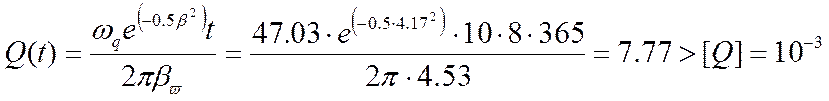
Розрахунок показав, що надійність гака недостатня.
Підбір нового діаметра гака шляхом зміни діаметра.
Новий
діаметр циліндричної частини: ![]()
Перевірка нового перерізу:
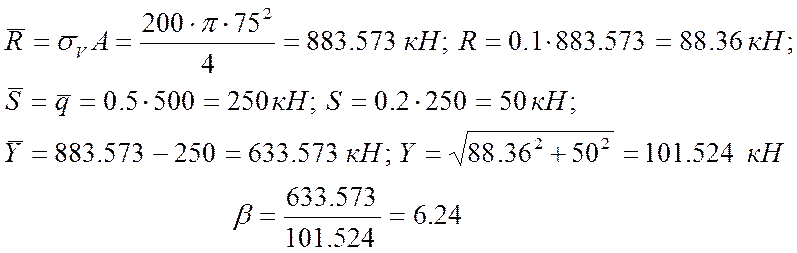
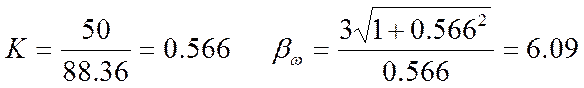
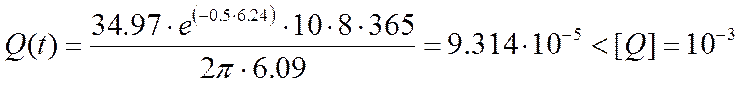
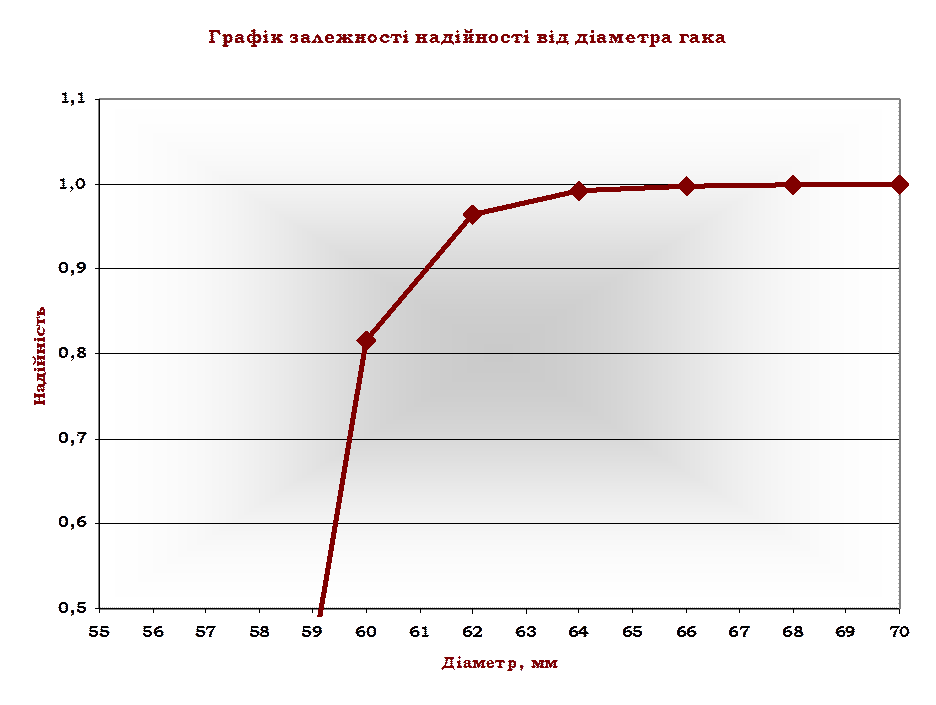
Надійність гака забезпечена.
|
Вихідні дані |
Характеристика резерву несучої здатності |
Імовірність відмови гака |
||||||||||||||||||||
|
Діаметр d, мм |
Вантажо-підйом-ність q, т |
Режим роботи |
Термін служби, років |
математичне сподівання навантаження q, т |
коефіцієнт варіації вантажу Vg |
ефективна частота, we |
Характеристики сталі |
Надійність |
Мат. споді-вання несучої здат-ності, кН |
Стандарт несучої здат-ності, кН |
Мат. сподівання навантажен-ня q, кН |
Стандарт наванта-ження, кН |
Резерв несучої здатності математич-ного сподівання |
Стандарт |
Характе-ристика безпеки, β |
Ефективна частота ВП Y(t), wg |
Коефіцієнт широкополосності, βw |
Імовірність відмови, Q(t) |
Надійність гака, P(t) |
Висновок |
||
|
sy - мат. очікуван-ня міцності сталі, МПа |
Vs - коеф. варіації сталі |
|||||||||||||||||||||
|
50 |
50 |
7К |
10 |
25 |
0,2 |
107 |
240 |
0,1 |
0,999 |
471 |
47,1 |
250 |
50 |
221 |
68,7 |
3,22 |
77,9 |
4,12 |
491,91449 |
-4,90914488159E+02 |
надійність недостатня |
|
|
52 |
50 |
7К |
10 |
25 |
0,2 |
107 |
240 |
0,1 |
0,999 |
510 |
51,0 |
250 |
50 |
260 |
71,4 |
3,64 |
74,9 |
4,28 |
108,98379 |
-1,07983786238E+02 |
надійність недостатня |
|
|
54 |
50 |
7К |
10 |
25 |
0,2 |
107 |
240 |
0,1 |
0,999 |
550 |
55,0 |
250 |
50 |
300 |
74,3 |
4,03 |
72,0 |
4,46 |
22,07351 |
-2,10735077226E+01 |
надійність недостатня |
|
|
56 |
50 |
7К |
11 |
25 |
0,2 |
107 |
240 |
0,1 |
0,999 |
591 |
59,1 |
250 |
50 |
341 |
77,4 |
4,41 |
69,1 |
4,65 |
4,63087 |
-3,63086568236E+00 |
надійність недостатня |
|
|
58 |
50 |
7К |
12 |
25 |
0,2 |
107 |
240 |
0,1 |
0,999 |
634 |
63,4 |
250 |
50 |
384 |
80,8 |
4,76 |
66,3 |
4,85 |
0,93191 |
6,80891894563E-02 |
надійність недостатня |
|
|
60 |
50 |
7К |
13 |
25 |
0,2 |
107 |
240 |
0,1 |
0,999 |
679 |
67,9 |
250 |
50 |
429 |
84,3 |
5,08 |
63,5 |
5,06 |
0,18439 |
8,15607135916E-01 |
надійність недостатня |
|
|
62 |
50 |
7К |
14 |
25 |
0,2 |
107 |
240 |
0,1 |
0,999 |
725 |
72,5 |
250 |
50 |
475 |
88,0 |
5,39 |
60,8 |
5,28 |
0,03663 |
9,63373919610E-01 |
надійність недостатня |
|
|
64 |
50 |
7К |
15 |
25 |
0,2 |
107 |
240 |
0,1 |
0,999 |
772 |
77,2 |
250 |
50 |
522 |
92,0 |
5,68 |
58,2 |
5,52 |
0,00743 |
9,92572209785E-01 |
надійність недостатня |
|
|
66 |
50 |
7К |
16 |
25 |
0,2 |
107 |
240 |
0,1 |
0,999 |
821 |
82,1 |
250 |
50 |
571 |
96,1 |
5,94 |
55,7 |
5,77 |
0,00156 |
9,98441371273E-01 |
надійність недостатня |
|
|
68 |
50 |
7К |
17 |
25 |
0,2 |
107 |
240 |
0,1 |
0,999 |
872 |
87,2 |
250 |
50 |
622 |
100,5 |
6,19 |
53,2 |
6,03 |
0,00034 |
9,99658148098E-01 |
надійність достатня |
|
|
70 |
50 |
7К |
18 |
25 |
0,2 |
107 |
240 |
0,1 |
0,999 |
924 |
92,4 |
250 |
50 |
674 |
105,0 |
6,41 |
50,9 |
6,30 |
0,00008 |
9,99921052960E-01 |
надійність достатня |
|
|
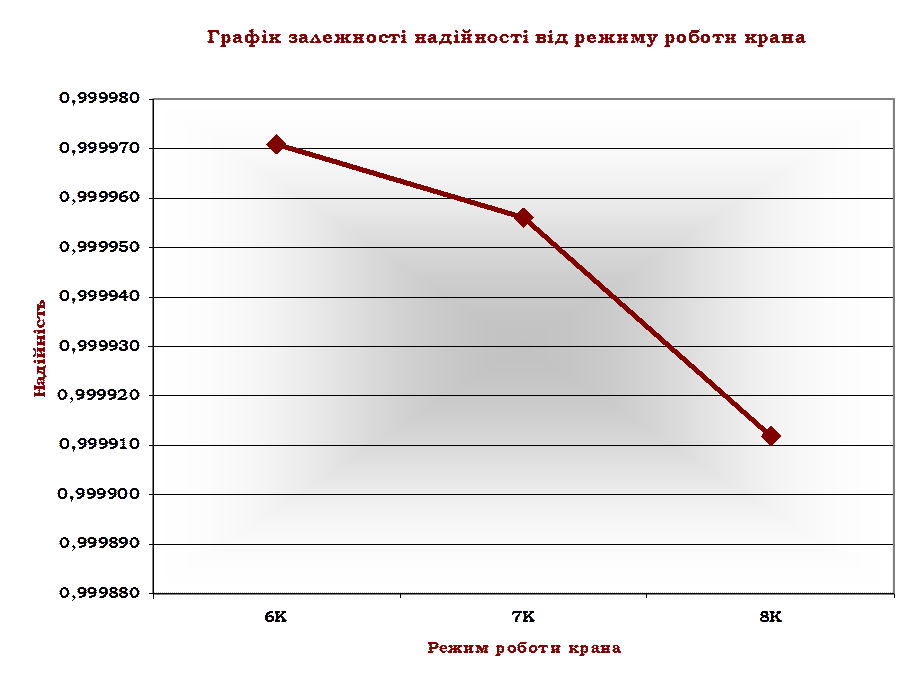
70 |
50 |
6К |
10 |
25 |
0,2 |
71 |
240 |
0,1 |
0,999 |
924 |
92,4 |
250 |
50 |
674 |
105,0 |
6,41 |
33,8 |
6,30 |
2,91030E-05 |
9,99970896989E-01 |
надійність достатня |
|
|
70 |
50 |
7К |
10 |
25 |
0,2 |
107 |
240 |
0,1 |
0,999 |
924 |
92,4 |
250 |
50 |
674 |
105,0 |
6,41 |
50,9 |
6,30 |
4,38595E-05 |
9,99956140533E-01 |
надійність достатня |
|
|
70 |
50 |
8К |
10 |
25 |
0,2 |
215 |
240 |
0,1 |
0,999 |
924 |
92,4 |
250 |
50 |
674 |
105,0 |
6,41 |
102,4 |
6,30 |
8,81288E-05 |
9,99911871165E-01 |
надійність достатня |
|
Задача 3. Підібрати переріз сталевої балки, що завантажена повторним навантаженням (за схемою незалежних випробувань), виходячи з нормативної ймовірності відмови [Q] .
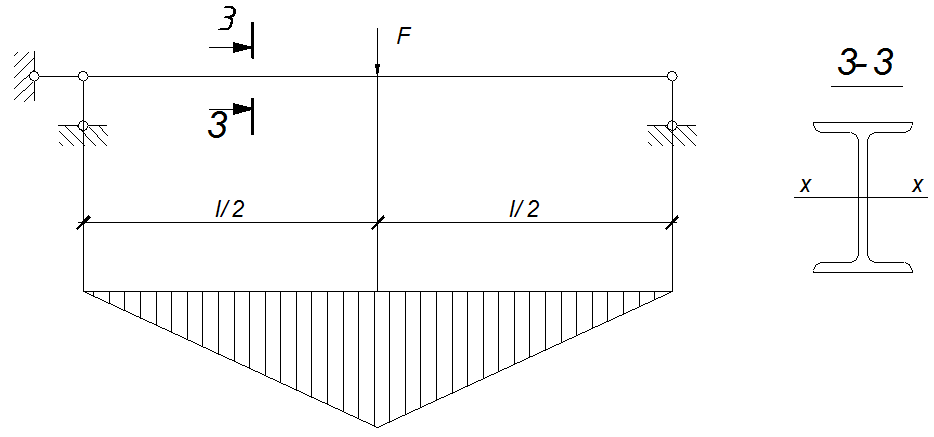
Математичне
сподівання навантаження ![]() , проліт балки ℓ=2,2м,
кількість циклів навантаження n=105,
[Q]=10-2; числові
характеристики втомної міцності сталі
, проліт балки ℓ=2,2м,
кількість циклів навантаження n=105,
[Q]=10-2; числові
характеристики втомної міцності сталі ![]() коефіцієнт
варіації навантаження VF=VS
=0.2, балка прокатна з двотавра з паралельними гранями
полиць згідно з сортаментом.
коефіцієнт
варіації навантаження VF=VS
=0.2, балка прокатна з двотавра з паралельними гранями
полиць згідно з сортаментом.
Характеристики зусилля (моменту) у балці:
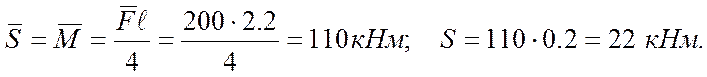
Характеристики безпеки β. Використаємо схему незалежних випробовувань, позначимо: P1 i Q1 –ймовірності безвідмовної роботи та відмови при окремому завантаженні (випробуванні), Pn i Qn – ті ж параметри після n випробовувань. Ці величини зв’язані співвідношеннями:
![]() (2)
(2)
З рівняння nQ1=[Q] для нормального розподілу виведемо формулу обчислення β:
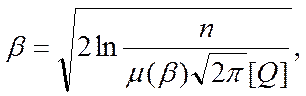 (3)
(3)
де
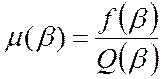 - інтенсивність розподілу, для
нормального закону при великих β μ(β)≈β.
- інтенсивність розподілу, для
нормального закону при великих β μ(β)≈β.
Рівняння (3) розв’язується підбором виходячи з умови μ(β)≈β, для даного прикладу маємо:
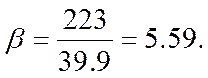
Підбір перерізу балки. Використаємо квадратне рівняння (1)
![]()
Необхідний момент опору балки:
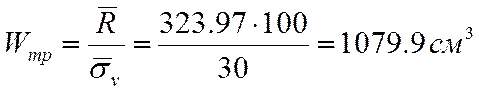
Приймаємо І45Б1. Wk=1110см3.
Перевірка прийнятого перерізу балки.
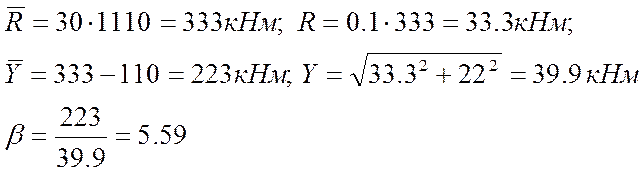
За таблицями нормального розподілу П-5-3 знаходимо
Q1=Q(β=5,59)=1.07·10-8.
За формулою (2) для n=105 випробувань маємо:
Qn=105·1.07·10-8=0,107·10-3<[Q]=10-3
Надійність балки забезпечена.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.