Проверим систему на устойчивость, для этого воспользуемся критерием Гурвица. За характеристическое уравнение примем знаменатель передаточной функции неизменяемой части и приравняем ее к нулю:
(13)
Обозначим:
а0 =1,2996 ×10-4 а1 = 2,28×10-2 а2 = 1 а3 = 0
У нас получилось уравнение третьей степени, поэтому главный определитель равен:
а1 а3
0
D ГЛ = а0 а2 0
0 а1 а3
Подставим числовые значения:
2,28×10-2
0 0
D ГЛ = 1,2996×10-4 1 0
0 2,28×10-2 0
Вычислим определители всех порядков:
D 0 = а0 =1,2996 ×10-4 > 0
D 1 = а1 = 2,28×10-2> 0
D 2 = 2,28×10-2 0 = 2,28×10-2> 0
1,2996×10-4 1
|
2,28×10-2 0 0
D 3 = 1,2996×10-4 1 0 = 0
0 -2,28×10-2 0
Так как старший определитель равен нулю, то система находится на границе апериодической устойчивости.
4.3.Построение переходного процесса и оценка качества системы
Для оценки качества системы построим переходный процесс для разомкнутой части с передаточной функцией:
WНЧ (р) =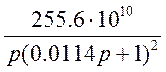
Если на вход подается единичная импульсная функция d(t), тогда входной сигнал равен:
(14)
Тогда импульсная переходная функция в изображении по Лапласу:
(15)
Найдем изображение по Лапласу передаточной функции неизменяемой части и входного сигнала:
WНЧ (р) =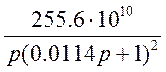
Тогда уравнение (15) примет вид:
W (р) =×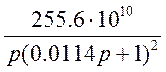
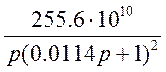1= (16)
Теперь перейдем от g(р) к g(t) с помощью обратного преобразования Лапласа:
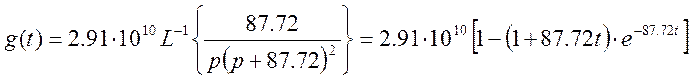(17)
И получим уравнение переходного процесса:
(18)
Задаваясь числовыми значениями t, составим таблицу значений переходного процесса (таблица 1).
Таблица 1
|
t |
g(t) |
t |
g(t) |
t |
g(t) |
t |
g(t) |
|
|
0.002 |
0.04 |
0.02 |
1.52 |
0.044 |
2.61 |
0.076 |
2.88 |
|
|
0.004 |
0.14 |
0.022 |
1.67 |
0.048 |
2.69 |
0.08 |
2.89 |
|
|
0.006 |
0.28 |
0.024 |
1.81 |
0.05 |
2.72 |
0.086 |
2.90 |
|
|
0.008 |
0.46 |
0.026 |
1.93 |
0.054 |
2.76 |
0.09 |
2.90 |
|
|
0.010 |
0.64 |
0.028 |
2.05 |
0.058 |
2.80 |
0.096 |
2.90 |
|
|
0.012 |
0.83 |
0.03 |
2.15 |
0.06 |
2.82 |
0.1 |
2.91 |
|
|
0.014 |
1.01 |
0.034 |
2.32 |
0.064 |
2.84 |
1.0 |
2.91 |
|
|
0.016 |
1.19 |
0.038 |
2.46 |
0.068 |
2.86 |
10.0 |
2.91 |
|
|
0.018 |
1.36 |
0.04 |
2.52 |
0.07 |
2.87 |
100.0 |
2.91 |
По данному уравнению (18) на рисунке 6 построим график.
Исходя из полученной импульсной переходной функции g(t) проведем оценку качества системы:
- Установившееся значение переходного процесса hУСТ = 2,91× 1010;
- Максимальное значение переходного процесса hУСТ = 2,91× 1010 ;
- Установившаяся ошибка d = 0,05 ×2,91× 1010 = 0,14× 1010 ;
- Время переходного процесса t n = 0,054 с;
- Время перерегулирования переходного процесса d % =0 %
Из графика на рисунке 6 и оценок качества видно, что система монотонна.
5. Анализ локальной системы с помощью логарифмических характеристик
5.1. Построение ЛАЧХ неизменяемой части
Передаточная функция неизменяемой части:
WНЧ (р) =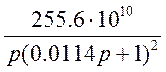
(12)
Пусть такт между непрерывной и дискретной частями равен:
То = 0,01 с
Данная система является дискретной, поэтому для построения ЛАЧХ нам нужно перейти к псевдочастоте l. А для этого уравнение (12) преобразуем согласно таблице z –преобразований:
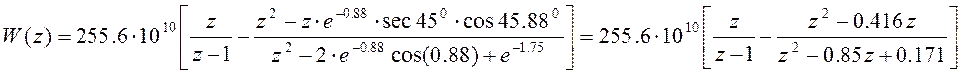
Домножим
предыдущее уравнение на фиксатор нулевого порядка (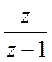
)
и получим:
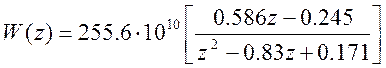(19)
Разложим знаменатель на множители, для этого приравняем его к нулю:
Получим, что уравнение (19) равно:
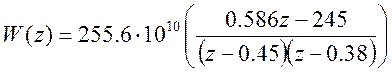(20)
Перейдем к w - преобразованиям, используя соотношение:
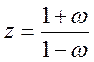
Тогда:
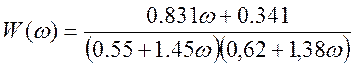(21)
Теперь перейдем к псевдочастоте по формуле:
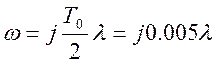(22)
Подставим и получим:
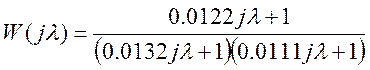(23)
Тогда постоянные времени из выражения (23) равны:
Т1 = 0,0122 с Т2 = 0,0132 с Т3 = 0,0111 с
А частоты сопряжения:
λ1
=
=82 с-1 λ 2
=
=76 с-1 λ
3 =
=90 с-1
(24)
Их логарифмы:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.