Для вибору оптимального порядку апроксимуючого полінома задаються деяким його початковим значенням, котре може бути вибране на основі вивчення графічного розміщення точок на плоскій системі координат.
Оцінку результатів апроксимації виконують наступними показниками :
Середня квадратична похибка:
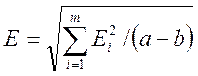(1.6)
Значення похибки:
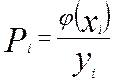(1.7)
Середня арифметичне значення:
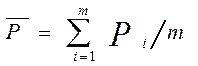(1.8)
Середнє квадратичне відхилення відношення P:
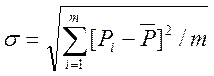(1.9)
Коефіцієнт варіації:
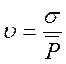(1.10)
2. Виконання апроксимації заданого емпіричного поля
2.1. Вихідні дані
2.2. Апроксимація за допомогою квадратичної функції
Апроксимація виконується функцією φ(x) = а0+а1 x+a2 x2
Таким чином
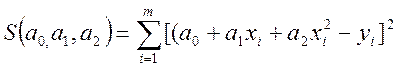(2.1)
Визначаємо частинні похідні і прирівнюємо їх до нуля
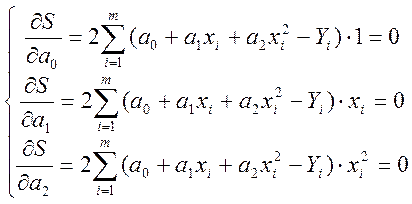(2.2)
Після спрощень:
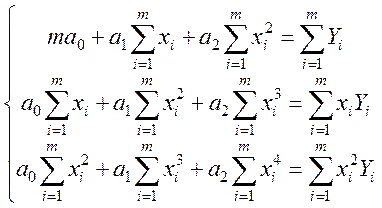(2.3)
2.3. Обчислення коефіцієнтів СЛАР МНК
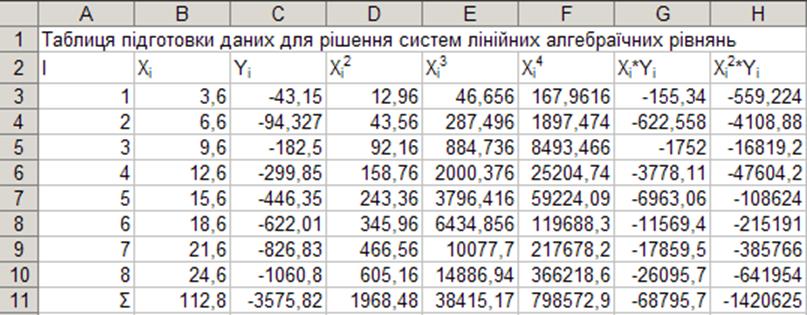
Ці дані були обраховані за такими формулами
|
№п/п |
х |
у |
х2 |
х3 |
|
1 |
3,6 |
-43,15 |
=B3^2 |
=B8^3 |
|
2 |
6,6 |
-94,327 |
=B4^2 |
=B9^3 |
|
3 |
9,6 |
-182,5 |
=B5^2 |
=B10^3 |
|
4 |
12,6 |
-299,85 |
=B6^2 |
=B11^3 |
|
5 |
15,6 |
-446,35 |
=B7^2 |
=B12^3 |
|
6 |
18,6 |
-622,01 |
=B8^2 |
=B13^3 |
|
7 |
21,6 |
-826,83 |
=B9^2 |
=B14^3 |
|
8 |
24,6 |
-1060,8 |
=B10^2 |
=B15^3 |
|
∑= |
=СУММ(B3:B10) |
=СУММ(C3:C10) |
=СУММ(D3:D10) |
=СУММ(E8:E15) |
|
х4 |
х*у |
х2*у |
|||
|
=B3^4 |
=B3*C3 |
=D3*C3 |
|||
|
=B4^4 |
=B4*C4 |
=D4*C4 |
|||
|
=B5^4 |
=B5*C5 |
=D5*C5 |
|||
|
=B6^4 |
=B6*C6 |
=D6*C6 |
|||
|
=B7^4 |
=B7*C7 |
=D7*C7 |
|||
|
=B8^4 |
=B8*C8 |
=D8*C8 |
|||
|
=B9^4 |
=B9*C9 |
=D9*C9 |
|||
|
=B10^4 |
=B10*C10 |
=D10*C10 |
|||
|
=СУММ(F3:F10) |
=СУММ(G3:G10) |
=СУММ(H3:H10) |
2.4. Розв’язання системи рівнянь МНК
Складемо матрицю системи
Визначник ми рахуємо за формулою =МОПРЕД(A14:C16). Визначник має не дорівнювати 0.
Рахуємо обернену матрицю використовуючи команду =МОБР(A14:C16). Так як це функція масиву, то спочатку потрібно виділити область оберненої матриці. У нас вона має такий вигляд:
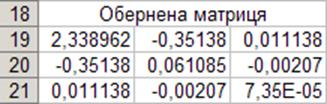
Знаходимо вектор невідомих коефіцієнтів. Перемножуємо обернену матрицю на вектор вільних членів:
Значення ми отримали за такими формулами:
Далі виконуємо перевірку: множимо матрицю системи на вектор невідомих за допомогою команди =МУМНОЖ(A14:C16;G19:G21). В результаті маємо отримати вектор вільних членів.
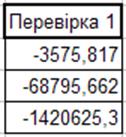
Вони дорівнюють значенню вектора вільних членів:
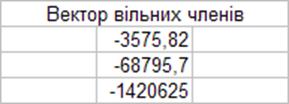
2) Множимо матрицю системи на обернену матрицю, використовуючи вбудовану функцію =МУМНОЖ(A14:C16;A19:C21). При цьому має вийти одинична матриця:
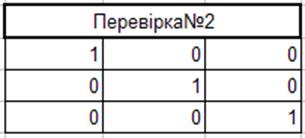
Отже невідомі знайдено правильно і можемо продовжувати. Апроксимуюча функція має вигляд: f(x)= - 12,5231 - 1,9087 x - 1,65627x².
3. Статистичний аналіз результатів
Обчислимо підсумкові дані за допомогою таблиці:
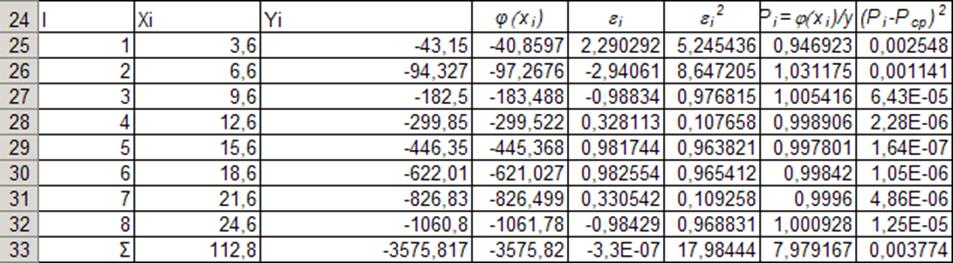
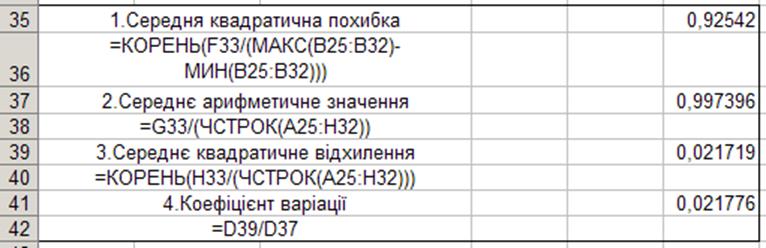
Ці дані ми отримали за такими формулами:
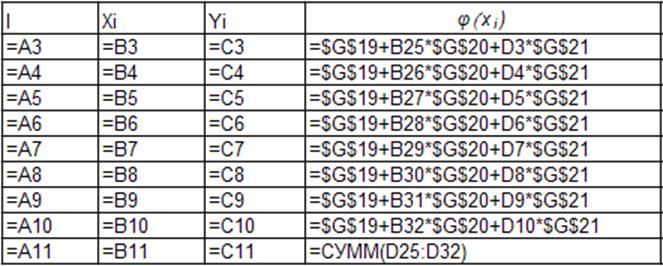
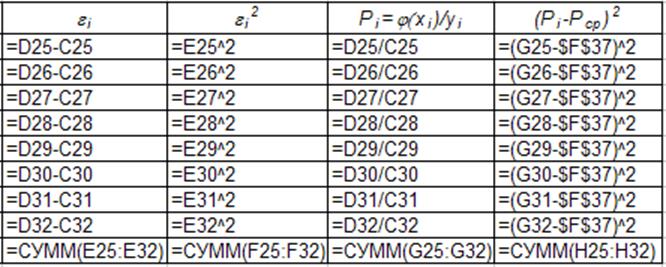
Отже, ми отримали всі дані, які потрібні для побудови діаграм і графіків, тому переходимо до графічної частини роботи.
4. Побудова графіків заданої й апроксимуючої функцій
Для побудови графіку виконаємо Вставка–Диаграмма.
Крок 1:
В полі вибору типу діаграми обираємо Точечная (Рис. 4.1)
Крок 2:
1) Обираємо діапазон х, у та φ(xі)– =' Рішення СЛАР'!$B$24:$D$32 (Рис. 4.2)
2) Присвоєння назви рядам (Рис. 4.3)
Крок 3:
Обираємо потрібні нам настройки – відключаємо допоміжні лінії та ін. (Рис. 4.4)
Крок 4:
Обираємо місце вставлення графіку – В отдельном листе (Рис. 4.5)
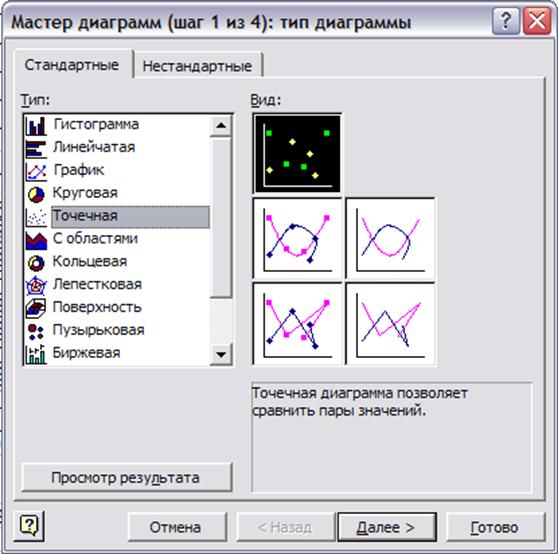
Рис. 4.1 Вибір типу діаграми
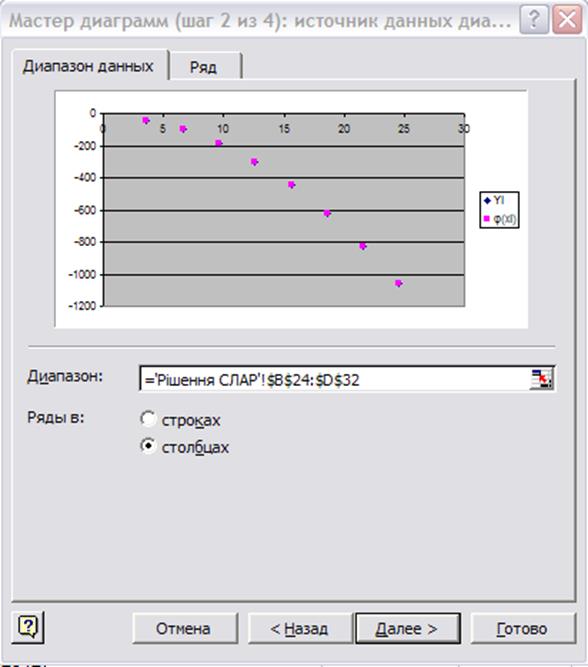
Рис 4.2 Вибір джерела даних
.
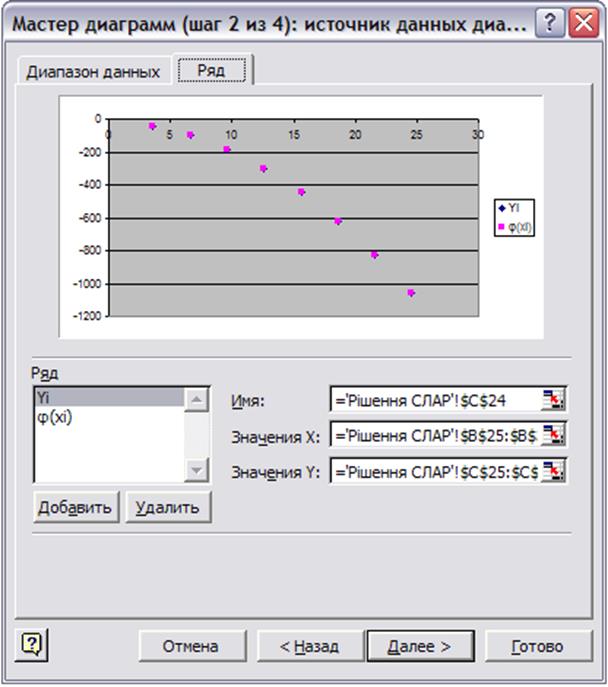
Рис 4.3 Присвоєння назви рядам
Рис. 4.4 Налаштування параметрів діаграм
Рис. 4.5 Вибір місця розташування
Отримуємо такий графік:
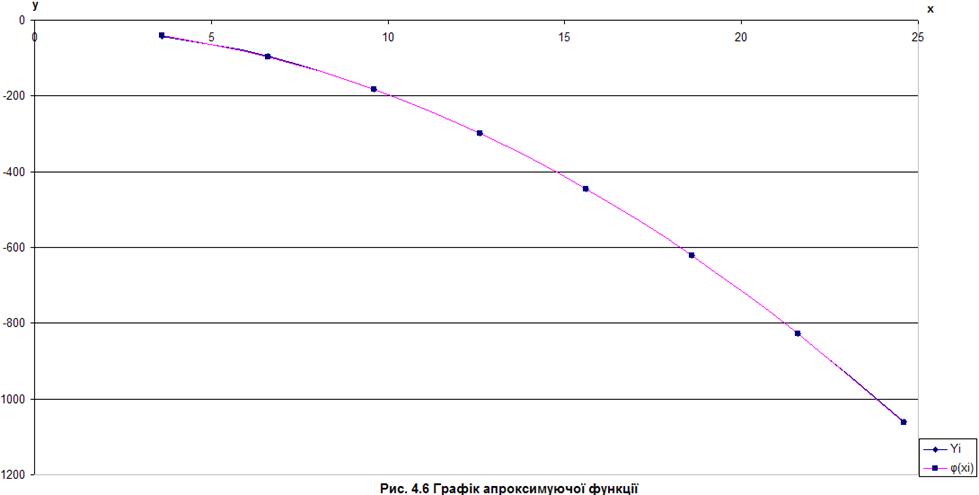
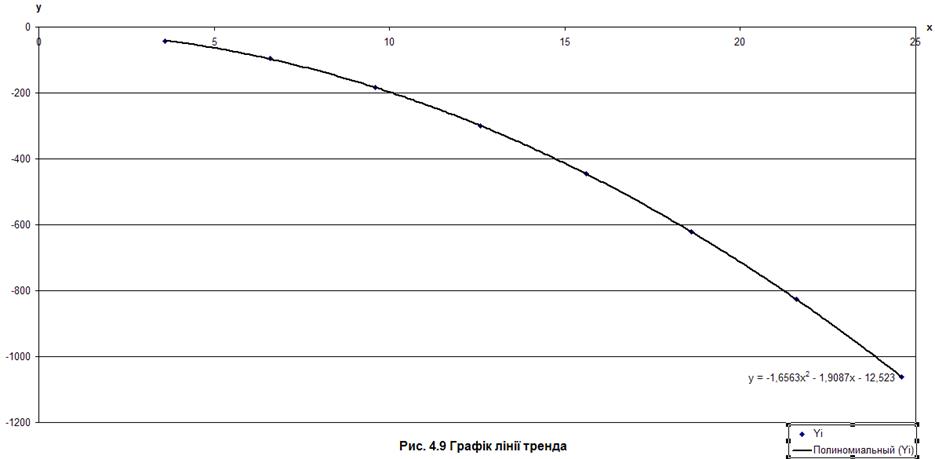
Тепер додаємо лінію тренда, як показано на Рис. 4.7, 4.8
Лінія тренда дозволяє перевірити чи правильно виконана апроксимація.
Для цього натискаємо Диаграмма/Добавить линию тренда. Вибираємо тип ПОЛИНОМИАЛЬНАЯ, СТЕПЕНЬ 2 (Рис 4.7). На вкладниці Параметры ставимо прапорець навпроти показывать уравнение на диаграмме (рис. 4.8). Після цього натискаємо на клавішу OKі отримуємо графік лінії тренда.
Рис. 4.7 Вибір типу лінії тренда
Рис. 4.8 Налаштування параметрів
ВИСНОВОК
Коефіцієнти полінома знайдені правильно, так як це підтвердили дві перевірки, які були виконані у розрахунковій частині роботи. Значення середнього квадратичного відхилення, середньої квадратичної похибки, середнього арифметичного значення, коефіцієнту варіації незначні, тому апроксимуюча функція φ(x) максимально наближено відображає задану функцію f(x). До цього ж висновку ми прийдемо, якщо проаналізуємо графічне зображення функцій. Це свідчить про те, що розрахунки зроблені вірно, діаграми і графіки побудовані правильно і основна задача досягнена.
Список використаних літературних джерел:
1.ДСТУ Б А.2.4-4-99. Система проектної документації для будівництва. Основні вимоги до робочої документації.— Введений на заміну ДСТУ Б А.2.4-4.95 наказом Держбуду України № 117 від 11.05.99р.; Чинний від 01.10.99.—Київ, 1999. — 59с.
2.Бронштейн И.Н., Семендяев К.А. Справочник по математике для инженеров и учащихся вузов. М.: Гостехиздат, 1956.—608с.
3.Львовский Е.Н. Статистические методы построения эмпирических формул: Учеб. Пособие.—М.: Высш школа, 1982. — 224 с.
4.Самарский А.А., Гулин А.В. Численные методы: учебное пособие для студентов вузов. – М.:Наука, 1989. – 318с.
5. Клименко В.И. Эффективный самоучитель работы на ПК. 2002.
6.Методичні вказівки до виконання лабораторних робіт на тему „Робота в табличному процесорі MS Excel 97”, О.І. Корх, Л.Ф. Крещенко, М.Є. Рогоза. – 1999.
7.Методичні вказівки до виконання лабораторних робіт на тему „Підготовка текстового документа у редакторі Microsoft Word”, О.А. Харченко, О.І. Сороковий. – 2002.
8.Турчак Л.И. Основы численных методов: Учеб. пособие для студентов вузов. – М.:Наука, 1987. – 318с.
9. Microsoft Excel. Шаг за шагом. - М.: ЭКОМ, 2001. - 472с.
10.Билл Каморда Использование Microsoft Word 97 - К.М.С-П., Вильямс, 1999. – 799с.
11.Клименко В.І. Конспект курсу лекций: 1-ша та 2-га частини.-1999, 2000.-280с.
12.Вальдр т О.Л., Чаловська Р.Б. Робота з Microsoft Excel 2000.-Київ: ЦУЛ, 2003.-294с.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
