Міністерство освіти і науки України
Полтавський національний технічний університет імені Юрія Кондратюка
Факультет будівельний
Кафедра будівельної механіки
РОЗРАХУНКОВО-ГРАФІЧНА РОБОТА № 1
із дисципліни «Інформатика» на тему:
«Апроксимація функцій методом найменших квадратів»
Залікова книжка № 07277
Виконав студент групи 110-Б
Масюк А.О.
Керівник :
Мартьянов В. В.
Полтава
2008
МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ
Полтавський національний технічний університет імені Юрія Кондратюка
Факультет будівельний
Кафедра будівельної механіки
Напрям підготовки –– 0601“Будівництво”
Освітньо-кваліфікаційний рівень – 6.060101– “Бакалавр”
Навчальна дисципліна – “Інформатика”
Семестр – 2
Група: 110-Б
Студент (студентка): Масюк А.О.
прізвище, ім'я, по-батькові
на розрахунково-графічну роботу № 1 на тему:
«Апроксимація функцій методом найменших квадратів»
Строки виконання РГР № 1: початок 10.03.2008 р. закінчення 04.04.2008 р.
1. За допомогою табличного процесора MS Excel виконати апроксимацію методом найменших квадратів експериментально отриманих табличних даних:
|
x |
3,6 |
6,6 |
9,6 |
12,6 |
15,6 |
18,6 |
21,6 |
24,6 |
|
y |
-43,150 |
-94,327 |
-182,50 |
-299,85 |
-446,35 |
-622,01 |
-826,83 |
-1060,8 |
Апроксимацію
виконати функцією, яка має вигляд ![]() .
.
2. Застосовуючи текстовий редактор MS Word створити звіт по розрахунково–графічній роботі, що містить:
2.1. Титульний аркуш;
2.2. Бланк завдання;
2.3. Зміст;
2.4. Розрахункову частину роботи (ця частина звіту повинна містити описання алгоритмів із розрахунковими формулами, уведеними за допомогою редактора формул), яка складається із наступних пунктів:
– апроксимація результатів експериментальних досліджень заданих у табличній формі методом найменших квадратів;
– розв‘язок системи лінійних алгебраїчних рівнянь для визначення коефіцієнтів апроксимуючого полінома методом оберненої матриці;
– статистичний аналіз отриманих результатів;
2.5. Графічну частину роботи – графіки апроксимуючої функції, лінії тренда та опис їх побудови;
2.6. Список використаних літературних джерел.
3. Текст звіту оформлюється шрифтом Times New Roman розміром 14 кегель з полуторним інтервалом і повинен бути вирівняним по ширині з абзацним відступом 1,25 см. Всі сторінки повинні бути пронумеровані. Нумерація сторінок проставляється у правому верхньому куті аркуша. Титульна сторінка і бланк завдання включаються до нумерації сторінок, але номери на них не проставляються. Звіт повинен бути оформлений у відповідності з вимогами ДСТУ Б А.2.4–4–99 і роздрукований на аркушах формату А4. До звіту додаються електронні копії робочої книги MS Excel із розрахунками і графіками та звіту підготовленому в текстовому редакторі MS Word.
При захисті роботи студент повинен відповісти на питання стосовно виконаної роботи та вміти користуватись інструментами MS Excel (форматування, обчислення, побудова графіків та ін.).
СтудентКерівник
підпис підпис
Зміст
1.Теоретичні основи метода найменших квадратів..........................................4
2. Виконання апроксимації заданого емпіричного поля даних.......................6
2.1. Вихідні дані.........................................................................................6
2.2. Апроксимація за допомогою квадратичної функції........................6
2.3. Обчислення коефіцієнтів СЛАР МНК..............................................7
2.4. Розв’язання системи рівнянь МНК....................................................8
3. Статистичний аналіз результатів...................................................................10
4. Побудова графіків заданої й апроксимуючої функцій................................11
Висновок.................................................................................................................16
Список використаних літературних джерел.......................................................17
|
Задача апроксимації
полягає у тому, що задану функцію f(x) необхідно замінити (апроксимувати)
деякою функцією φ(x) так, щоб відхилення функції φ(x) від f(x)
у заданій області було найменшим: 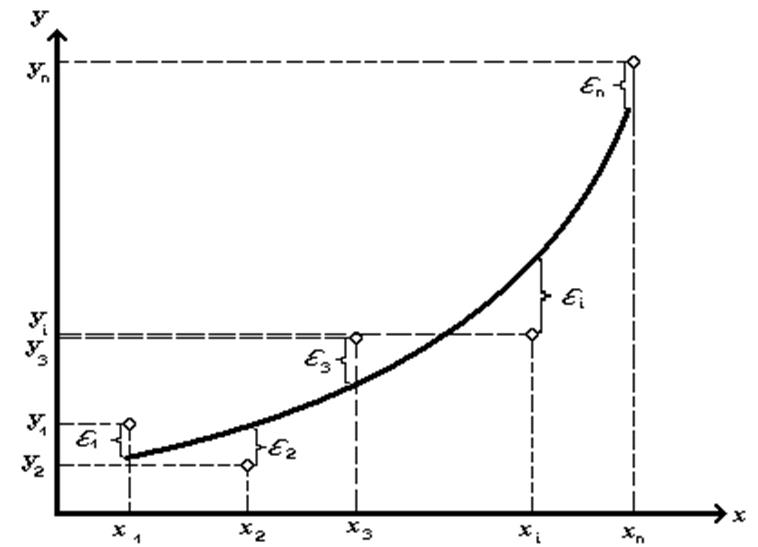
При цьому функцію φ(x) називають апроксимуючою. m – кількість точок, а n – ступінь полінома. На практиці найбільш важливою є апроксимація многочленом (поліномом):
φ(x) = а0+а1 x+a2 x2+…+an xn (1.1)
У подальшому нас цікавитиме лише така апроксимація. При цьому необхідно підібрати коефіцієнти а1, а2, ... аn таким чином, щоб досягти найменшого відхилення апроксимуючої функції від заданої. Про так зване найменше відхилення ми поговоримо пізніше. У залежності від того, що ми будемо розуміти під найменшим відхиленням, будемо мати й різні методи апроксимації.
Якщо наближення будувати на заданій дискретній множині точок xi, то апроксимація називається точковою. Один із основних типів точкової апроксимації - інтерполяція. Інтерполяція полягає у тому, що для заданої функції y=f(x) необхідно побудувати многочлен φ(x) = а0+а1 x+a2 x2+…+an xn, що одержує у заданих точках xi ті ж значення yi, що і задана функція f(x), тобто
φ(xi) = f(xi) при і =1,... m.
Точки xi називаються вузлами інтерполяції, а многочлен φ(x) інтерполяційним многочленом. Табличні експериментальні дані одержані, як правило шляхом вимірювань і містять похибки. Побудова апроксимуючого многочлена з умовою обов‘язкового його проходження через експериментальні точки означала б ретельне повторення тих помилок, які вже містяться у таблично заданих значеннях. Вихід можна знайти, будуючи многочлен якомога меншого ступеню, який не перетинає всі точки, а проходить дуже близько до заданих точок.
Коли ступінь многочлена дорівнює кількості точок, маємо інтерполяцію, якщо n < m - має місце згладжування.
За міру відхилення апроксимуючої функції від заданої найчастіше на практиці обирають суму квадратів відхилень апроксимуючої функції від заданої у всіх точках, тобто величину
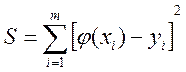 (1.2)
(1.2)
При побудові апроксимуючого многочлена необхідно підібрати такі коефіцієнти а0, а1, ... аn, щоб величина S була мінімальною. Ця процедура реалізована у методі найменших квадратів.
Запишемо суму квадратів відхилень апроксимуючої функції від заданої для всіх точок x0, x1, x2 …, xm:
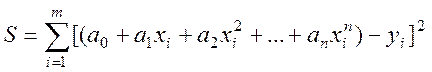 (1.3)
(1.3)
Параметри а0, а1, ... аn - коефіцієнти многочлена, знаходяться з умови мінімума функції S. Мінімум функції має місце тоді, коли часткові похідні за незалежними змінними дорівнюють нулю:
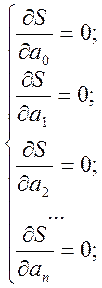 (1.4)
(1.4)
Ці співвідношення - система лінійних алгебраїчних рівнянь для визначення коефіцієнтів а0, а1, ... аn.
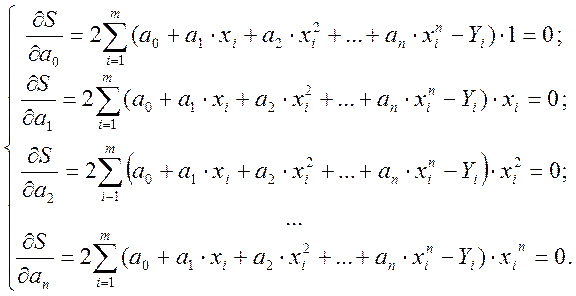 (1.5)
(1.5)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.