Для одного объекта проектирования разрабатывается несколько математических моделей, различной степени сложности и точности.
Математические модели бывают на 3-х уровнях описания объекта:
1. Микроуровень – описание состояния сплошных сред, из которых состоит объект. Математическая модель представляет собой уравнение математической физики, с соответствующими начальными и граничными условиями.
Как правило, это дифференциальные уравнения в частных производных:
L(φ(z)) = f(z) – это общий вид диф. ур.
L – диф. оператор.
φ(z) – функция отражающая внутреннюю природу объекта.
z – вектор независимых переменных.
z = {x, y, z, t}.
f(z) – функция, которая отражает внешние воздействия или выходной параметр.
На микроуровне могут располагаться несколько фазовых переменных.
Рассмотрим математическую модель гидроэлектрического поляризационного преобразователя расхода (ГЭППР).
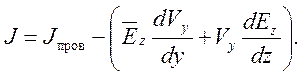- стационарное двухмерное уравнение
второго порядка.
Макроуровень
Здесь непрерывное пространство разбивается на дискреты, и от полей фазовых переменных переходят к вектору фазовых переменных (каждая переменная рассматривается отдельно на дискрете). В качестве мат. модели используются обыкновенные дифференциальные уравнения. Модели макроуровня как правило проще моделей микроуровня.
Например: при рассмотрении ГЭППР на макроуровне в уравнение входят только напряженность Е и ее производная – сила тока I.
Системный уровень
На этом уровне составляются модели более сложных объектов, потому принимаются следующие допущения: из описания объекта исключается пространственная координата, предполагается прохождение сигнала только в одну сторону, не учитывается влияние нагрузки.
Например: мат. моделью ГЭППР будет являться апериодическое звено первого порядка:
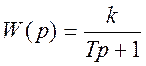, где к=10-3,
Т=10-4.
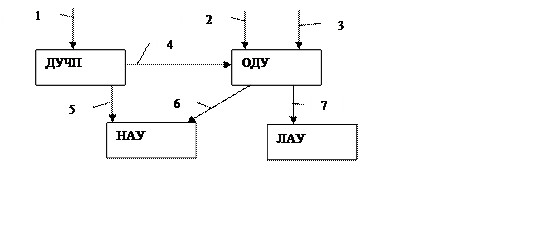Алгоритм преобразования мат. модели в
последовательность элементарных операций
1 – микроуровень;
2 – макроуровень;
3 – системный уровень;
4 – преобразование динамических ДУЧП (дифференциальных уравнений в частных производных) в ОДУ (обычные диф. уравнения);
5 – преобразование статических ДУЧП в НАУ (нелинейные алгебраические уравнения);
6 – преобразование нелинейных ОДУ в НАУ методом численного интегрирования;
7 – преобразование линейных ОДУ в ЛАУ (линейные алгебраические уравнения).
Переход от алгебраического уравнения к последовательности элементарных операций производится методом итерации.
Дискретные математические модели
Непрерывное время t разбивается на дискреты Dt=ti+1-ti. В общем виде дискретная мат. модель имеет вид: Ut=F(Ut-1,V) – состояние объекта в последний момент времени зависит от состояния объекта в предыдущий момент времени и входного сигнала в текущий момент.
Для комбинационных схем: Ut=F(V) – состояние объекта зависит только от входного сигнала.
Дискретные мат. модели рассматриваются только на макроуровне или в случае необходимости на системном уровне.
Алгоритм получения мат. модели
1. определение свойств, которые должна отражать мат. модель;
2. сбор сведений об объекте моделирования;
3. составление уравнений, определение свойств объекта и составление алгоритмов и программы;
4. расчет
и определение точности мат. модели, задача проектировщика – найти такие
значения внутренних переменных, для которых выполняется условие: min E(м), x'x(D) – ошибка должна быть минимальной
при условии, что все параметры находятся в допустимой области. Ошибка мат.
модели определяется по формуле: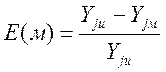 
, значение
выходного параметра определяется по ТЗ.
5. определение области адекватности мат. модели:
-
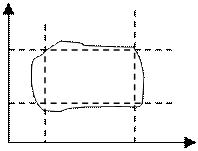для удобства расчетов фактическую область адекватности сводят к прямоугольной.
Для каждого объекта могут быть использованы упрощенные модели с меньшей точностью и более точные модели, которые как правило менее экономичны. Упрощенные модели используются на начальных этапах проектирования, а более сложные – на окончательных этапах.
Численные методы одновариантного анализа
Численные методы разделяются на прямые и итерационные.
Прямой метод. Метод Гаусса
Для нахождения вектора внутренних переменных используется метод Гаусса. Сначала из уравнений исключается часть переменных, и матрица из прямоугольной преобразуется в верхнетреугольную:
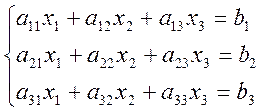
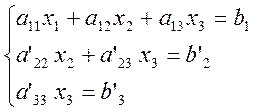
Итерационный метод
(позволяет получить приближенное значение неизвестных) – метод деления отрезка пополам на начальном этапе и более точный метод Ньютона.
Метод деления отрезка пополам:
хk – шаг итерации.
х* - искомое значение переменной.
Значение переменной на следующем шаге зависит от значения переменной на предыдущем шаге.
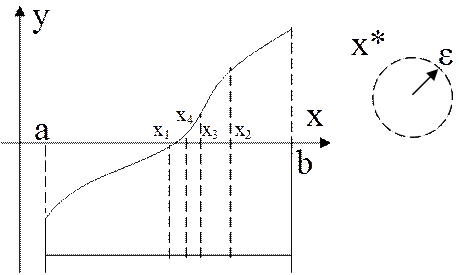
Данный метод имеет высокую сходимость, т.е. быстро попадает в окрестность искомой точки.
Метод Ньютона:
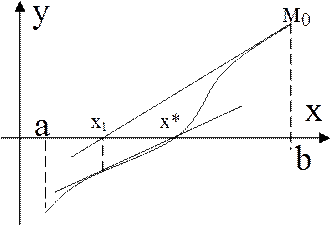
М0 – начальная точка.
Через начальную точку проводим касательную и находим точку первого приближения, из этой точки опускаем перпендикуляр.
Итерационные методы могут быть использованы не только для одновариантного анализа но и для задач оптимизации.
Необходимо найти такое значение вектора переменной, для которого параметр будет оптимальным (метод градиент – сопряженных градиентов).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.