4. Силовой расчет
Основной задачей силового расчета механизма является определение сил, действующих на звенья механизма, давления в кинематических парах и уравновешивающей силы на звене, принятом за ведущее. Решение этих задач позволяет располагать данными для прочностных расчётов звеньев, элементов кинематических и определения мощности двигателя привода.
При проведении силового расчёта предполагается, что трение в кинематических парах отсутствует.
4.1 Определение сил, действующих на звенья механизма.
Силы тяжести:
GАВD = 550 Н, GВC = 90 Н, GDF = 100 Н, GF = 200 Н
Силы сопротивления перемещению ползуна:
Диаграмма сил, действующих на ползун F (![]() )
)
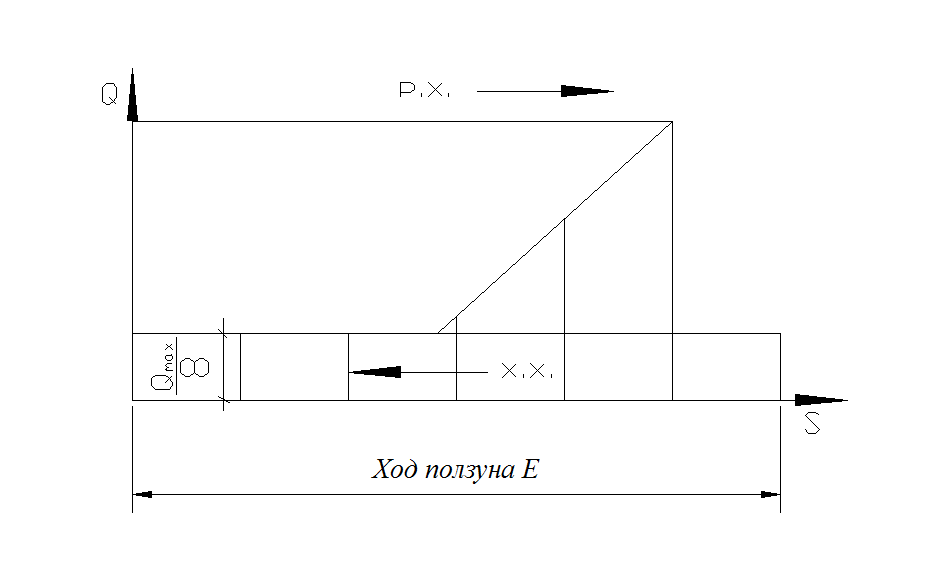
Во пятом положении ![]()
Сила Q направлена противоположно скорости VF.
4.2 Величины сил инерции:
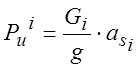
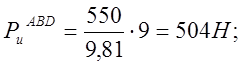
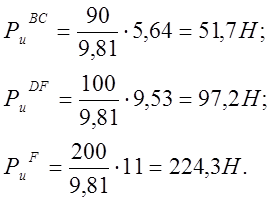
Эти силы прикладываем к центрам тяжести соответствующих звеньев и направляем противоположно направлению вектора ускорения центра тяжести.
4.3 Моменты от сил инерции звеньев:
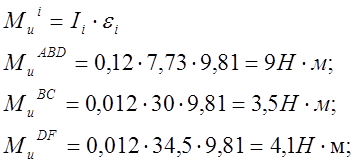
![]()
4.4 Определение реакций в кинематических парах.
Силовой расчёт механизма начинаем с диады DF – F, на которую действуют известные по величине и направлению силы веса GF и GDF, силы инерции РиF и РиDF, момент МиDF от сил инерции и сила сопротивления Q. Эту группу Ассура освобождаем от связей и вместо них прикладываем в точуку D реакцию Р4-2, а в точку F – реакцию Р0-5 (обе реакции неизвестны ни по величине, ни по направлению).
![]()
![]() Реакцию
Р4-2 раскладываем на две взаимно перпендикулярные составляющие
Реакцию
Р4-2 раскладываем на две взаимно перпендикулярные составляющие ![]() и
и ![]()
![]() .
.
Запишем уравнение моментов всех сил, действующих на звено DF, относительно точки F:
![]()
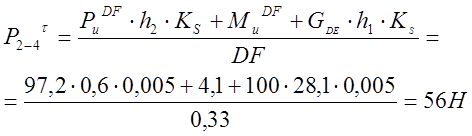
Далее, приняв масштаб сил ![]() по
векторному уравнению равновесия сил для группы:
по
векторному уравнению равновесия сил для группы: ![]() строим
план сил. По этому плану находим величины и направления сил Р2-4n
и Р0-5, а также полную реакцию в паре D
строим
план сил. По этому плану находим величины и направления сил Р2-4n
и Р0-5, а также полную реакцию в паре D
– Р2-4:
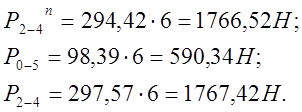
Причем ![]()
![]()
![]()
![]()
![]() Переходим
к силовому расчету группы Ассура DВA – ВC. Прикладываем все известные силы, освобождаем её от связей
и прикладываем реакции Р1-2 и Р0-3, которые неизвестны ни
по величине, ни по направлению. Реакцию Р1-2 раскладываем на
Переходим
к силовому расчету группы Ассура DВA – ВC. Прикладываем все известные силы, освобождаем её от связей
и прикладываем реакции Р1-2 и Р0-3, которые неизвестны ни
по величине, ни по направлению. Реакцию Р1-2 раскладываем на ![]() и
и ![]()
![]() , аналогично Р0-3 – на
, аналогично Р0-3 – на ![]() и
и ![]()
![]() .
.
Составим уравнение моментов всех сил, действующих на звено ВC, относительно точки В:
![]()
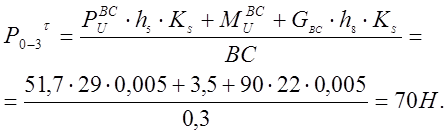
Составим уравнения моментов всех сил, действующих на звено АВD, относительно точки В:
![]()
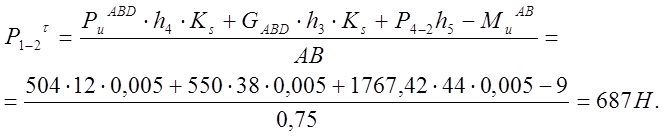
Приняв масштаб сил ![]() строим план сил
для всей диады АВ – ВD согласно векторному уравнению:
строим план сил
для всей диады АВ – ВD согласно векторному уравнению:
![]()
Из плана сил находим величины и направления сил Р0-3n и Р1-2n, а также полные реакции в кинематических парах Р1-2 и Р0-3.
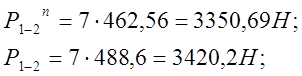
Причём Р1-2 = - Р2-1 = 3420.2 Н.
Переходим к силовому расчёту ведущего звена. Для определения давления Р0-1 в кинематической паре, образованной ведущим звеном со стойкой, необходимо уравновесить все силы, действующие на ведущее звено. Поэтому к ведущему звену прикладываем все действующие на него силы и в точку К прикладываем уравновешивающую силу Ру под углом 20º к касательной.
Величину уравновешивающей силы Ру находим из уравнения моментов относительно точки О всех сил, действующих на звено ОА:
![]()
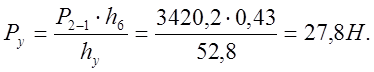
Приняв масштаб ![]() , строим план сил
для ведущего звена согласно векторному уравнению:
, строим план сил
для ведущего звена согласно векторному уравнению: ![]() .
.
Из плана сил находим величину и направление силы ![]()
Определение уравновешивающей силы методом профессора Н.Е. Жуковского.
Строим план скоростей во пятом положении и прикладываем в соответствующие точки этого плана все силы, действующие на данный механизм, предварительно повернув план скоростей на угол 90º. Рассматривая план скоростей как жёсткий рычаг, который находится в равновесии, возьмем сумму моментов всех перенесённых сил относительно полюса:
![]()
![]()
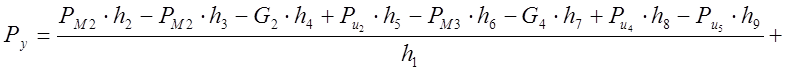
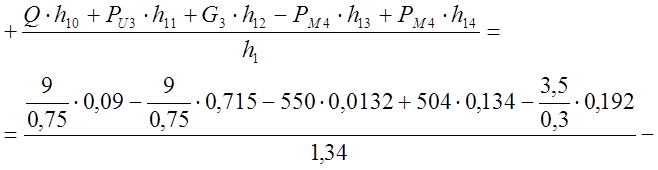
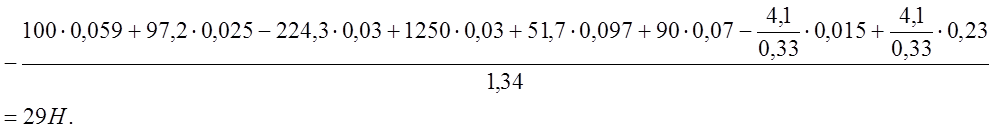
Результаты силового расчёта по методу Н.Г. Бруевича
|
Сила |
Р0-1 |
Р1-2 |
Р0-3 |
Р2-4 |
Р0-5 |
Ру |
|
Величина, Н |
3292 |
3420,2 |
2122,4 |
1767,42 |
590,34 |
27,8 |
По методу профессора Н.Е. Жуковского Ру = 29 Н (погрешность от определения величины уравновешивающей силы разными методами составляет 4,14 %).
5. Синтез кулачкового механизма
Построение диаграмм механизма.
Синтез кулачкового
механизма начинаем с построения заданной диаграммы 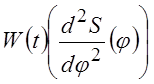 .
Интегрируя дважды эту диаграмму, получаем диаграммы
.
Интегрируя дважды эту диаграмму, получаем диаграммы 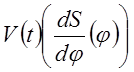 и
и
![]()
5.1 Определяем масштабы диаграмм:
Масштаб перемещения толкателя :
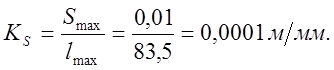
Масштаб оси абсцисс диаграмм движения толкателя:
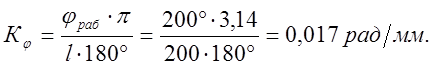
Масштаб оси ординат диаграммы 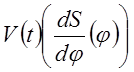 :
:
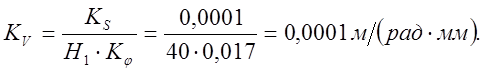
Масштаб оси ординат диаграммы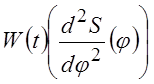 :
:
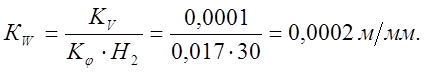
Принимаем, что кулачек вращается равномерно, т.е. ω = const.
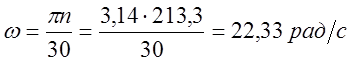
Масштаб времени:
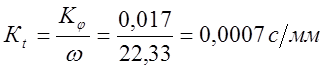
5.2 Определение минимального радиуса кулачка.
Для определения минимального радиуса-вектора теоретического
профиля кулачка строим диаграмму 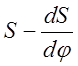 следующим
образом:
следующим
образом:
а) на траектории центра ролика толкателя отмечаем его положение 0, 1, 2, 3 и т.д. в соответствии с диаграммой перемещений и выбранным масштабом;
б) из каждой точки проводим отрезки ![]() в
направлениях, перпендикулярных движению центра ролика толкателя;
в
направлениях, перпендикулярных движению центра ролика толкателя;
в) концы отрезков ![]() соединяем плавной
кривой;
соединяем плавной
кривой;
г) проводим касательные к полученной кривой под углом ![]() к оси
к оси ![]() .
Точка пересечения этих касательных даёт нам область, где находится
радиус-вектор профиля кулачка. Отступаем расстояние смещения равное 0,01, т.к.
кулочек со смещенным центром. Кратчайшее расстояние между полученной областью и
кривой равно минимальному радиусу-вектору
.
Точка пересечения этих касательных даёт нам область, где находится
радиус-вектор профиля кулачка. Отступаем расстояние смещения равное 0,01, т.к.
кулочек со смещенным центром. Кратчайшее расстояние между полученной областью и
кривой равно минимальному радиусу-вектору ![]() теоретического
профиля кулачка.
теоретического
профиля кулачка.
Диаграмма 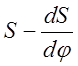 служит и для
определения углов передачи в каждом положении толкателя: угол
служит и для
определения углов передачи в каждом положении толкателя: угол ![]() образован здесь отрезком
образован здесь отрезком ![]() и прямой, соединяющей конец отрезка
и прямой, соединяющей конец отрезка ![]() с нанесенным на диаграмму центром
вращения кулачка.
с нанесенным на диаграмму центром
вращения кулачка.
5.3 Профилирование кулачка.
Кулачок профилируется методом обращенного движения.
а) Строим окружность радиусом ![]() и
радиусом равным величинесмещения центра кулочка r=10мм
и
радиусом равным величинесмещения центра кулочка r=10мм
б) делим рабочий угол ![]() на 25 частей и
получаем точки 1´, 2´,3´ и т.д.;
на 25 частей и
получаем точки 1´, 2´,3´ и т.д.;
в) проводим касательные к окружности r=10мм из точкам 1´, 2´,3´ и т.д.;
г) проводим окружности радиусом (![]() )
в каждом положении и получаем точки пересечения этих окружностей с
касательными;
)
в каждом положении и получаем точки пересечения этих окружностей с
касательными;
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.