![]()
![]()
![]()
![]() (3)
(3) ![]()
![]()
![]()
![]()
![]() (4)
(4) ![]()
![]()
Векторные уравнения для нахождения ускорения точки F имеют следующий вид:
![]()
![]()
![]()
![]() (5)
(5) ![]()
![]()
![]()
![]()
![]() (6)
(6) ![]()
![]()
Для положения 5:
![]()
![]()
![]()
![]()
![]()
Для положения 10:
![]()
![]()
![]()
![]()
![]()
2.7 План ускорений
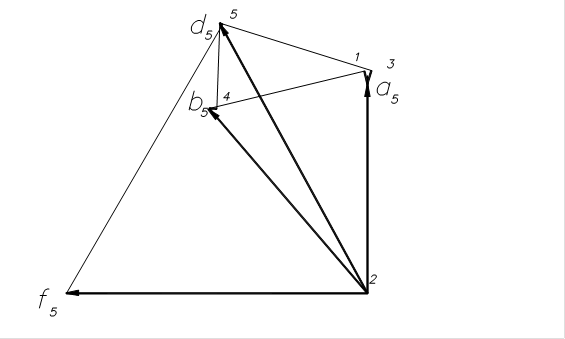
2.8 Ускорения точек звеньев механизма
Таблица 3
|
Ускорение а, м/с2 |
Положения механизма |
|
|
5 |
10 |
|
|
аА |
7,7 |
7,7 |
аВ |
8,9 |
6,6 |
аD |
11,3 |
5,88 |
aF |
11 |
3,74 |
|
аS2 |
9 |
6,57 |
|
аS3 |
5,64 |
3,32 |
|
аS4 |
9,53 |
4 |
|
аS5 |
11 |
3,74 |
2.9 Определение угловых ускорений механизма
![]()
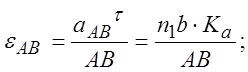
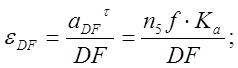
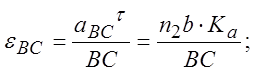
![]()
2.10 Угловые ускорения звеньев механизма
Таблица 4
|
Угловое ускорение ε, рад/с2 |
Положение механизма |
|
|
5 |
10 |
|
|
εАВ |
7,73 |
2,56 |
εВD |
30 |
22,1 |
|
εDF |
34,5 |
16,82 |
3. Синтез эвольвентного зубчатого зацепления
При выполнении этого листа, мы решаем следующие задачи:
1. рассчитываем и вычерчиваем эвольвентное зубчатое зацепление пары зубчатых колёс;
2. строим диаграммы относительных скоростей скольжения и удельных скольжений.
3.1 Для синтеза зубчатого зацепления используются следующие данные:
· m = 8 – модуль;
· z1 = 15, z2=32 – числа зубьев сопряженных колёс;
· параметры инструментальной рейки (исходного контура):
- α = 20º - угол профиля;
- hа* = 1 – коэффициент высоты зуба;
- c* = 0,25 – коэффициент радиального зазора.
3.2 Определение основных параметров передачи и размеров зубьев сопряженных зубчатых колёс
3.2.1 Радиусы делительных окружностей:
![]() мм
мм
![]() мм
мм
3.2.2 Радиусы основных окружностей:
![]() мм
мм
![]() мм
мм
3.2.3 Делительный окружной шаг:
![]() мм
мм
3.2.4 Делительная окружная толщина зуба:
![]() мм
мм
![]() мм
мм
3.2.5 Угол зацепления:
![]()
![]()
3.2.6 Межосевое расстояние
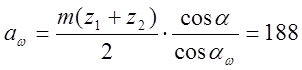 мм
мм
3.2.7 Радиусы начальных окружностей:
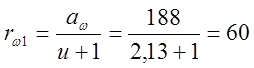 мм
мм 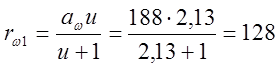 мм
мм 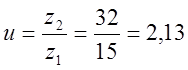
3.2.8 Радиусы окружностей впадин:
![]() мм
мм
![]() мм
мм
3.2.9 Радиусы окружностей вершин:
![]() мм
мм
![]() мм
мм
3.2.10 Шаг по основной окружности (основной шаг):
![]() мм
мм
3.2.11 Коэффициент перекрытия:
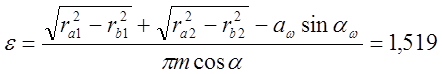
Зубчатое зацепление выполняем в масштабе (лист 2):
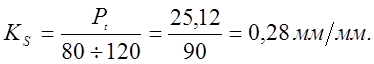
3.3 Построение зубчатого зацепления производим в следующей последовательности:
1. Проводим линию центров и откладываем межосевое расстояние;
2. Проводим начальные окружности (rω1, rω2), касающиеся в полюсе зацепления (точка Р), и основные окружности (rb1, rb2);
3. Через полюс зацепления (точку Р) проводим общую касательную к обеим окружностям, согласовав её направление с принятым направлением вращения зубчатых колес. Точки касания общей касательной с основными окружностями зубчатых колес определяют длину теоретической линии зацепления (АВ);
4. Через полюс зацепления (точку Р) проводим перпендикуляр к линии центров;
5. На линии зацепления вблизи полюса выбираем точку касания профилей К (точки Р и К совпадают);
6. Строим эвольвенту первого колеса:
а) отрезок КА делим на несколько равных частей и нумеруем полученные точки в направлении от точки К цифрами 0, 1, 2… и т.д. (точки 0 и К совпадают), за точкой А на продолжении линии КА откладываем несколько таких же отрезков;
б) отрезки такой же длины и в том же количестве откладываем от точки А в обе стороны по дуге основной окружности, пронумеровав их цифрами 0', 1', 2' и т.д.
в) к найденным точкам 0', 1', 2' и т.д. на основной окружности проводим из центра колеса радиальные прямые и перпендикулярные к ним касательные, изображающие последовательные положения отрезка КА в процессе перекатывания его по основной окружности;
г) на касательной в точке 1 откладываем длину одного отрезка К1, на касательной в точке 2 – длину двух отрезков К1 и т.д.;
д) соединив плавной кривой последовательные положения точки К, получающиеся при перекатывании прямой КА по основной окружности, вычерчиваем эвольвенту, определяющую профиль зуба первого колеса;
7. Проводим делительную окружность (радиус r1), а также окружности вершин (радиус rа1) и впадин (радиус rf2) первого колеса;
8. Профиль зуба на участке между основной окружностью и окружностью выступов вычерчиваем эвольвентой, а на участке между основной окружностью и окружностью впадин условно вычерчиваем радиальной прямой, сопрягающейся радиусом ρ = 0,3m = 5 мм с окружностью впадин;
9. Откладываем по дуге делительной окружности шаг Рt и толщину st1 зуба первого колеса, находим середину зуба, отложив дугу st1/2, соединяем её с центром колеса и проводим ось симметрии зуба;
10. Пользуясь симметрией, строим другой профиль зуба первого колеса, а также ещё один – два зуба;
11. В последовательности, оговоренной в пп. 6 – 10, строим профиль зуба второго колеса и не менее двух – трёх зубьев для него;
12. Находим точки a и b, ограничивающие длину практической линии зацепления, и на одном зубе каждого колеса выделяем рабочие участки эвольвентных профилей. По величине отрезка ab определяем коэффициент перекрытия:
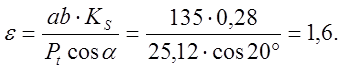
При сравнении со значением, полученным по расчётам, получаем погрешность:
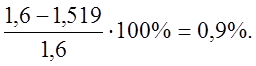
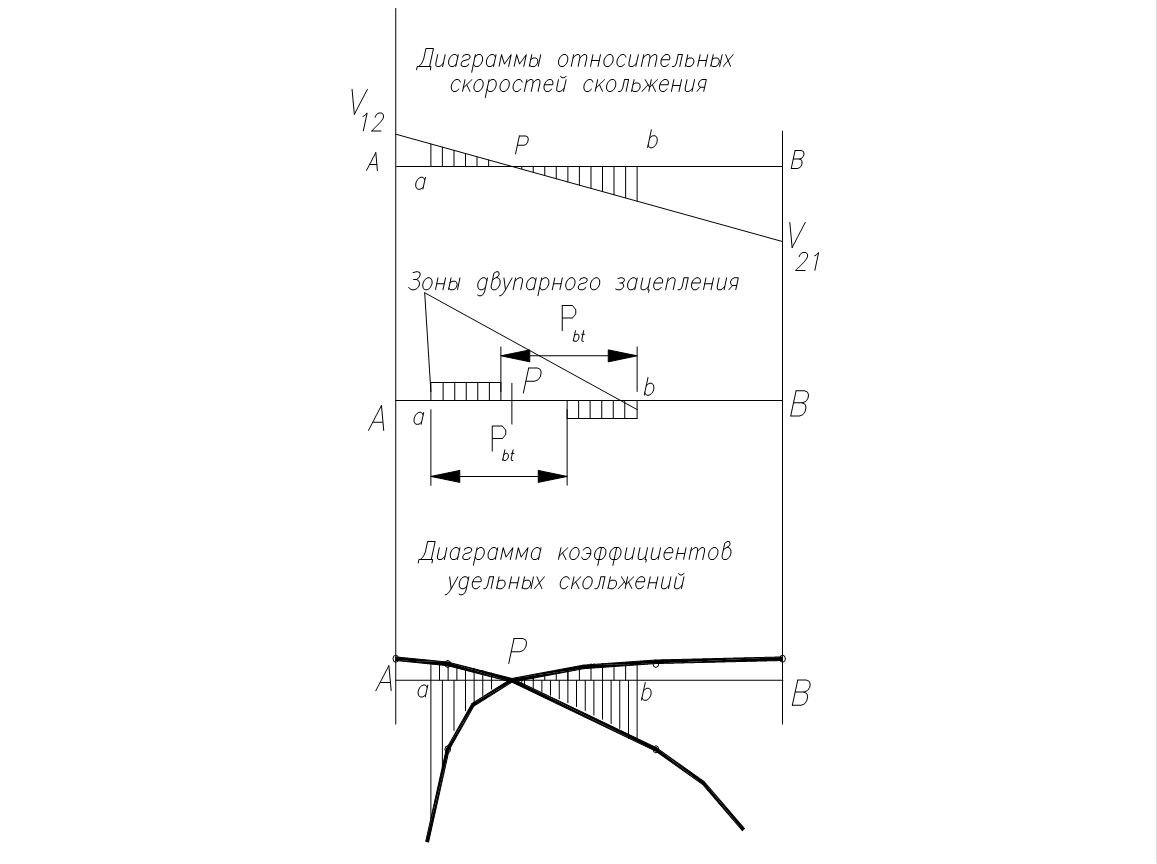
4. Диаграммы относительных скоростей скольжения и коэффициентов удельных скольжений.
Определяем значение относительной скорости скольжения:
![]()
Коэффициенты удельного скольжения рассчитываем по формулам:
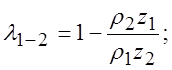
![]()
![]()
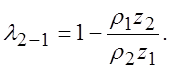
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.