Петербургский Государственный Университет Путей Сообщения
Исследование плоскопараллельного потенциального поля
Методические указания к лабораторной работе
Санкт-Петербург
2003
Цель работы -ознакомление с методом моделирования электростатического поля полем в проводящей среде.
Поле в диэлектрике в области, где нет свободных зарядов и поле в проводящей среде в области, где нет сторонних ЭДС, описываются одним и тем же уравнением Лапласа.
![]()
Так как решение уравнения Лапласа при заданных граничных условиях является единственным, то при одинаковых граничных условиях в диэлектрике и в проводящей среде распределения потенциалов будут одинаковыми. Это обстоятельство положено в основу моделирования электростатических полей полями в проводящих средах. Такое моделирование, как экспериментальный метод исследований, используют в тех случаях, когда задачу не удается решить аналитически (например, при сложной конфигурации проводников и диэлектриков).
В работе рассмотрены 2 случая
1-й – моделирование поля системы, для которой известно аналитическое решение (поля между двумя цилиндрами);
2-й – моделирование поля, аналитическое решение которого неизвестно
Исследование поля двух параллельных цилиндров одинакового радиуса
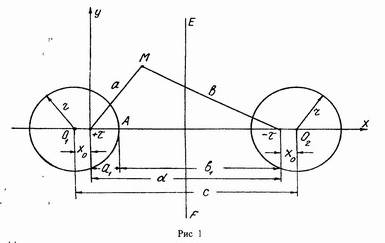
Аналитический расчет поля двух параллельных цилиндров одинакового радиуса приведен в курсе ТОЭ и сводится к следующему. Поле двух цилиндров исследуется на основе рассмотрения поля двух заряженных осей, так как поверхности параллельных цилиндров можно считать поверхностями равного потенциала двух заряженных осей, находящихся внутри цилиндров. Положение осей с линейной плотностью заряда + τ и – τ (рис.1) определяется с помощью формулы :
![]()
Где х0 – расстояние между центром цилиндра (например, О1) и соответствующей заряженной осью (+ τ)
С – расстояние между центрами цилиндров О1 и О2;
r – радиус цилиндров.
Потенциал в произвольной точке М в поле двух заряженных осей равен:
![]()
где εа = 8,85 . 10-12 Ф/м – диэлектрическая проницаемость воздуха,
![]()
- отношение рассояний от заряженных осей до точки М (см. рис. 1).
Разность потенциалов между двумя произвольными точками М1 и М2 в рассматриваемом поле составляет:
![]()
Чтобы приращение потенциала при переходе от одной линии равного потенциала к соседней оставалось постоянным, должно соблюдаться условие:
![]()
При известных потенциалах цилиндров
![]()
и выбранном приращении потенциала ΔU поле двух проводящих цилиндров рассчитывается в следующем порядке.
1. По формуле (2) вычисляется τ. Для определения k и U берется точка А на поверхности левого цилиндра (см. рис. 1):
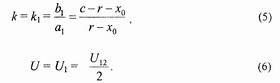
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.