Другие предметы \ Основы теории надежности

Оценка работоспособности систем тягового электроснабжения с учетом надежности ее основных элементов, страница 4

Для экспоненциального закона распределения принимается интенсивность отказов величиной постоянной:

Тогда вероятность безотказной работы вычисляется по формуле:

Таблица 2.2

Результаты расчетов параметров надежности при экспоненциальном законе распределения

t

f(t)

P(t)

Q(t)

1   

0

0,05563

1

0

2   

8,988001198

0,033741216

0,606529139

0,393470861

3   

17,9760024

0,020465031

0,367877597

0,632122403

4   

35,95200479

0,007528626

0,135333926

0,864666074

5   

53,92800719

0,002769613

0,04978632

0,95021368

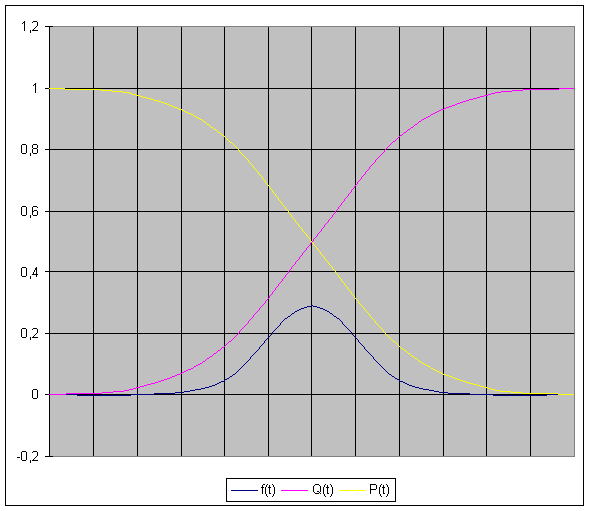
 Рис. 3

Зависимость числовых характеристик от времени при нормальном законе распределения

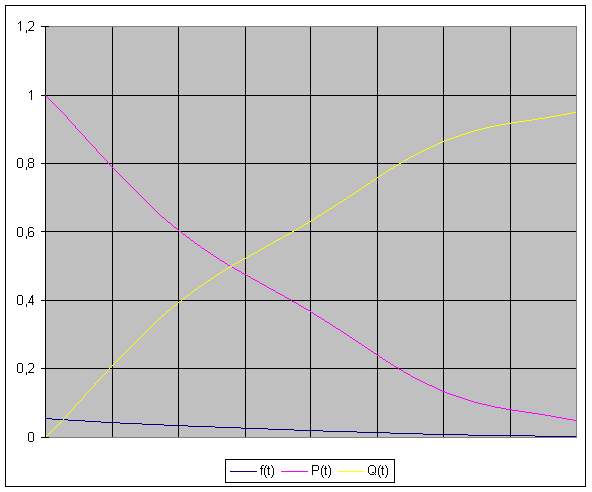
Рис. 4

Зависимость числовых характеристик от времени при экспоненциальном законе распределения

3.  Определение доверительных интервалов для числовых оценок параметров надежности P(t), Q(t), f(t), λ(t)

Для оценок параметров надежности P(t), Q(t), f(t), λ(t), рассчитанных в главе 1, вычислить и построить доверительные интервалы для заданной доверительной вероятности. Интервалы наносятся на графики, построенные в главе 1.

Доверительная вероятность β=0,82. Оператора Лапласа x=Ф-1(β)=0,95.

Определение доверительного интервала для λ(t)

Определение оценки (среднего значения):

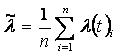, n=10

Определение несмещенной оценки (дисперсии, вычисленной по опытным данным):

Скачать файл