Оценка работоспособности систем тягового электроснабжения с учетом надежности ее основных элементов, страница 3

Построение графических зависимостей вероятности безотказной работы P(t), вероятности отказа Q(t), функции плотности распределения  времени безотказной работы f(t) и интенсивности отказов λ(t).

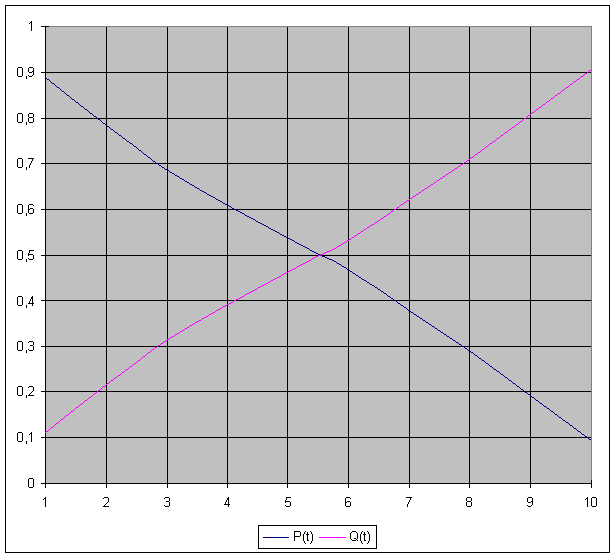
Рис. 1

Графические зависимости вероятности безотказной работы P(t) и вероятность отказа Q(t).

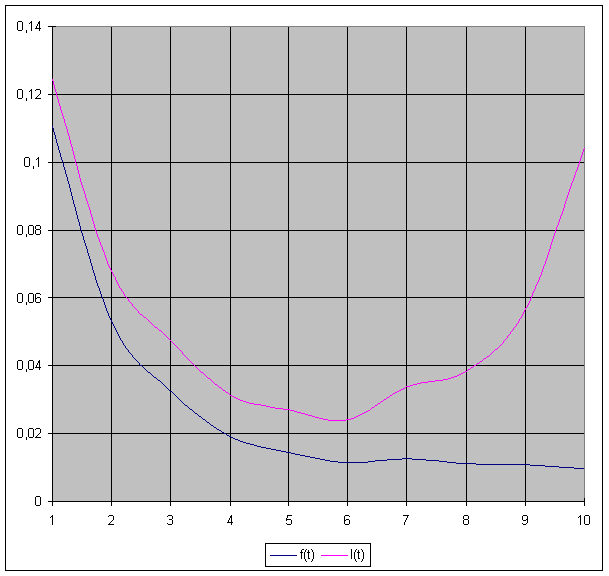
Рис. 2

Графические зависимости интенсивности отказов λ(t) и функции плотности распределения времени безотказной работы f(t).

2.  Расчеты числовых характеристик времени безотказной работы элементов при экспоненциальном и нормальном законах распределения

Tcp = 4,899

Нормальный закон распределения является предельным законом для случайных величин, которые имеют другие законы распределения и случайным образом воздействует на объект. Нормальный закон распределения в теории надежности используется для определения погрешностей. Для нормального закона задается функция плотности времени распределения безотказной работы:

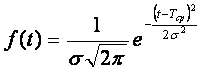
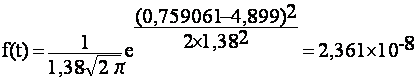
Вероятность отказа Q(t) определяется с помощью таблиц Лапласа.

Вероятность безотказной работы:

Интенсивность отказов:

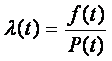
Таблица 2.1                

Результаты вычислений параметров надежности при нормальном законе распределения

t	f(t)	Q(t)	P(t)	l(t)
0,759061	2,36199E-08	0	1	2,36199E-08
2,139061	0,000204593	0,0228	0,9772	0,000209367
3,519061	0,047144502	0,1587	0,8413	0,056037683
4,899061	0,288999999	0,5	0,5	0,577999998
6,279061	0,047129381	0,8413	0,1587	0,296971525
7,659061	0,000204462	0,9772	0,0228	0,008967634
9,039061	2,35972E-08	1	0	0