Министерство образования Российской Федерации
Уральский государственный технический университет – УПИ
филиал в г. Краснотурьинске
кафедра вычислительной техники
по учебно-вычислительной практике
преподаватель: Мезенцева О.В.
студент: Бурлов А.С.
группа: Р-231КТ
2003
Тема: «Нахождение с заданной точностью корня уравнения F(x)=0 на промежутке [a;b] методом касательных (Ньютона)»
Контрольный пример: F(x)=0.9x^3-7x^2+5.9x+1.5 на [-1;8]
Условие задачи:
Для данной функции F(x) методом табулирования на интервале [a;b] локализовать корни уравнения F(x)=0 (т.е. выделить по возможности наименьшие отрезки, содержащие по одному корню). Найти эти корни методом касательных. Каждый корень вычислить дважды (с разной точностью). Все приближения к корню записывать в массив, который затем вывести на печать. Предусмотреть построение графика функции на заданном интервале.
Содержание
Введение……………………………………………………………………………4
1. Теоретическая часть…………………………………………………………….5
2. Описание структуры программы………………………………………………7
3. Входные и выходные данные………………………………………………….12
Заключение………………………………………………………………………..15
Приложение……………………………………………………………………….16
Цель работы: Изучить метод касательных (Ньютона) и составить программу, которая бы находила с заданной точностью корень F(x)=0.9x^3-7x^2+5.9x+1.5 на промежутке [a;b] методом касательных (Ньютона), а также построить график данной функции.
1. Теоретическая часть
Метод табулирования
Данный метод используется для локализации корней на заданном интервале и заключается в следующем:
1. Определяются границы интервала [a;b], выбирается шаг изменения аргумента х заданной функции – h;
2. Начальное значение аргумента – левая граница интервала (x1=h), за следующее значение аргумента – начальное значение плюс шаг (x2=x1+h);
3. Вычисляется значение функции от x1 – y1(x1);
4. Проверяется, не превышает ли x2 правой границы интервала [а;b]; если нет, то вычисляется значение функции от x2 – y2(x2), иначе конец процесса;
5. Проверяются знаки значений функции на границах отрезка [x1;x2], если знаки разные, то найденный отрезок содержит корень уравнения иначе нет;
6. Переход к следующему отрезку: x1=x2, x2=x1+h, y1=y2 и на пункт №3.
Метод касательных (Ньютона)
В этом способе вместо хорд проводятся касательные и ищут пересечение оси Ох с касательной, проведённой к линии y=f(x) в одной точки А или В.
Геометрический смысл:
Выясним, в какой из двух точек А или В надо проводить касательную. Для этого разберём всевозможные варианты знаков f'(x) и f''(x):
считаем, что f'(x) и f''(x) сохраняют знаки (предполагается, что f'(x) – непрерывна и имеет непрерывные производные f'(x) и f''(x)).
|
1 |
2 |
3 |
4 |
|
|
|
+ возрастающая |
+ возрастающая |
- убывающая |
- убывающая |
|
|
выпуклость вниз + вогнутость вверх |
Выпуклость вверх - вогнутость вниз |
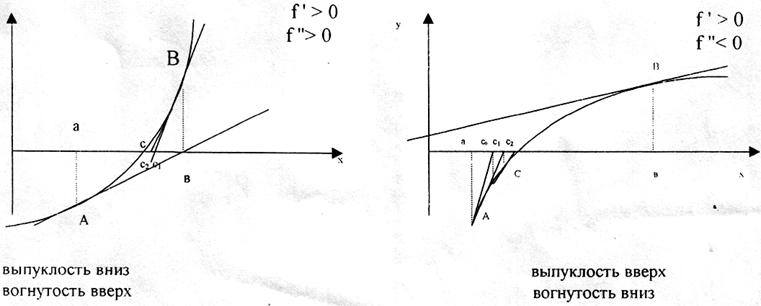
выпуклость вниз + вогнутость вверх |
выпуклость вверх - вогнутость вниз |
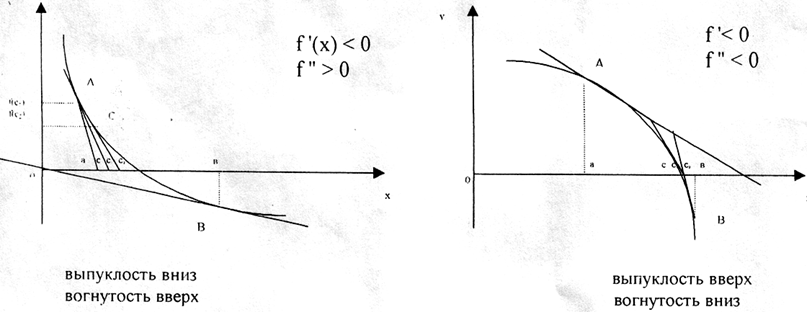 |
||
 |
||
Из рисунков видно, что касательную нужно проводить в том из концов дуги АВ, в котором ордината f(x) имеет тот же знак, что и знак второй производной.
![]() – уравнение касательной, проведённой
к кривой f(x) в точке с координатами с0 и f(с0).
– уравнение касательной, проведённой
к кривой f(x) в точке с координатами с0 и f(с0).
Отсюда найдём следующие приближения корня с1, как абсциссу точки пересечения касательной с осью Ох (y=0).
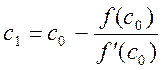
Аналогично могут быть найдены и следующие приближения, как точки пересечения с осью абсцисс касательных, проведённых в следующих точках.
Формула для n-го приближения имеет вид:
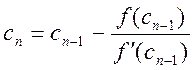 (f'(сn-1)≠0)
(f'(сn-1)≠0)
Для окончания
итерационного процесса может быть использовано условие ![]() или
условие близости двух последних приближений:
или
условие близости двух последних приближений: ![]() ,
где с0, c1, cn – приближения
значения корня по недостатку.
,
где с0, c1, cn – приближения
значения корня по недостатку.
2. Описание структуры программы
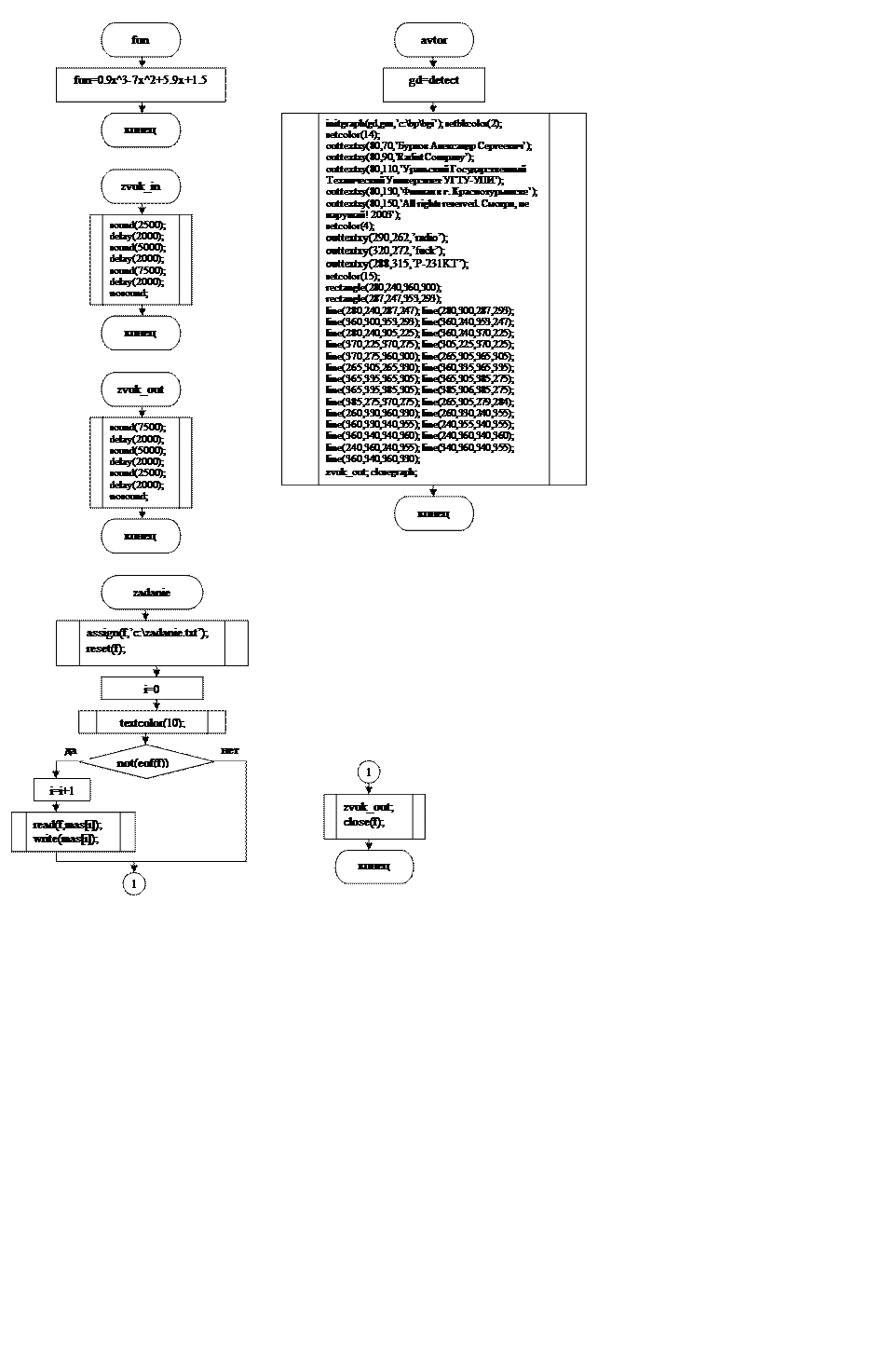
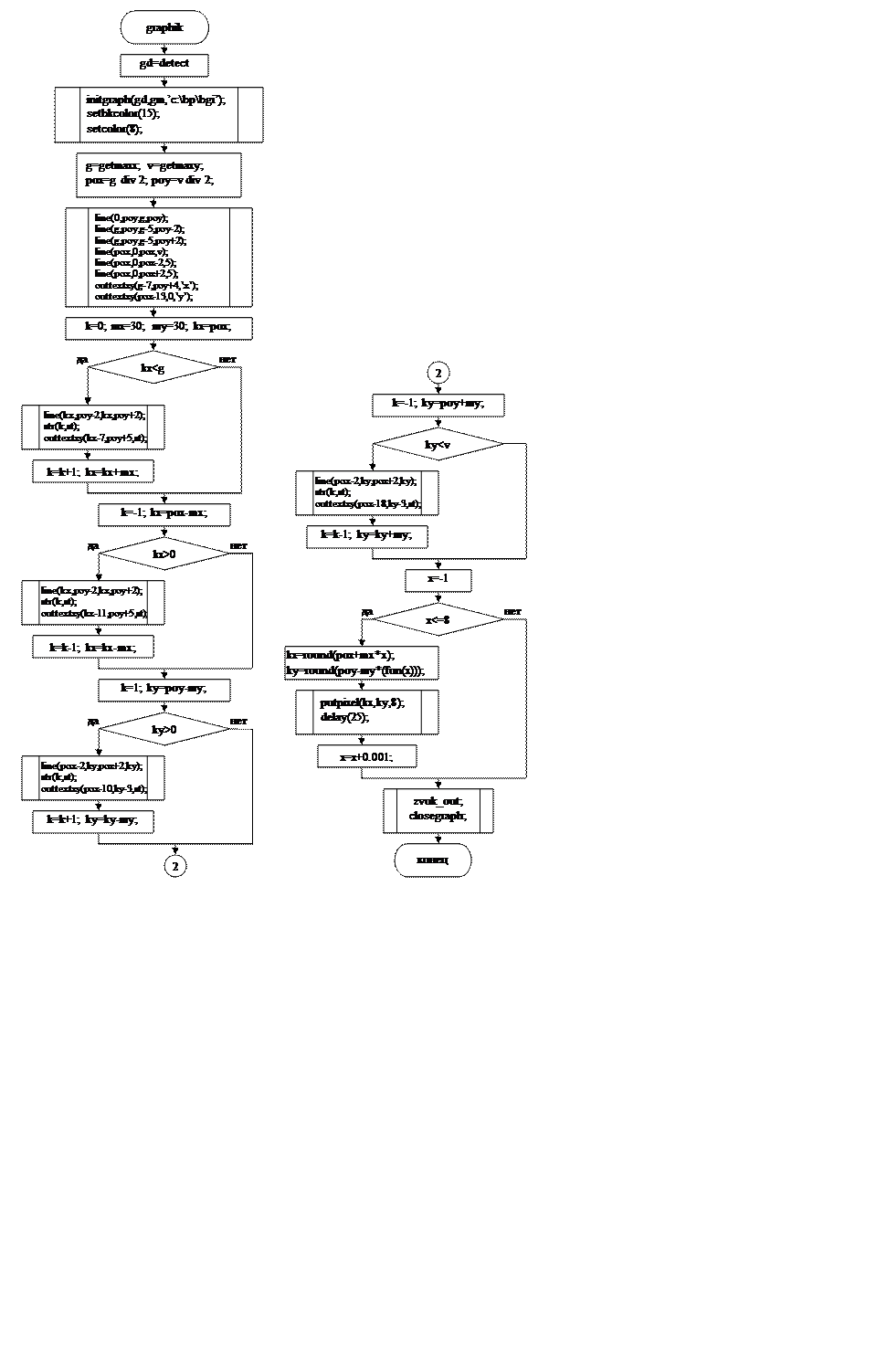
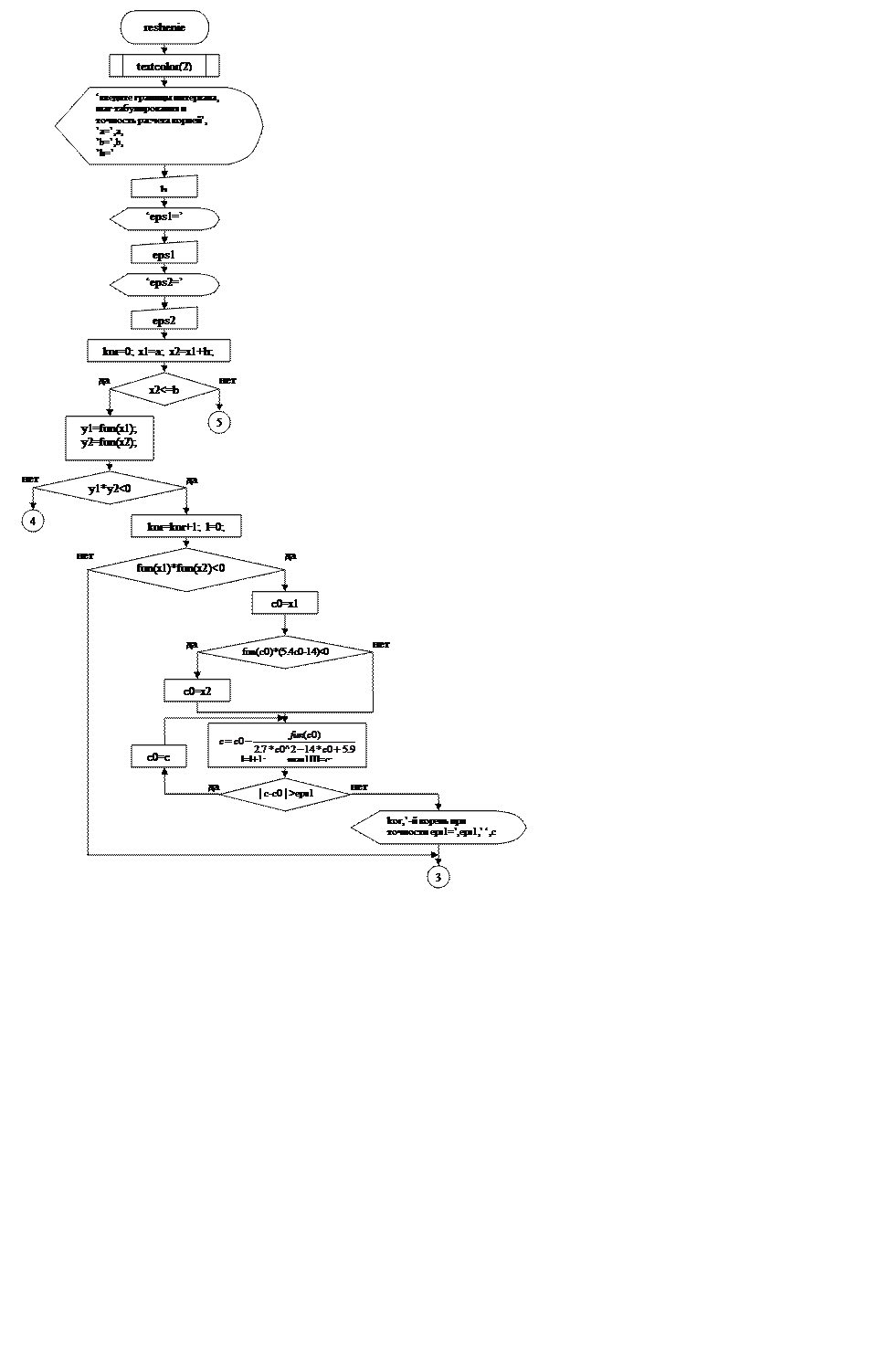
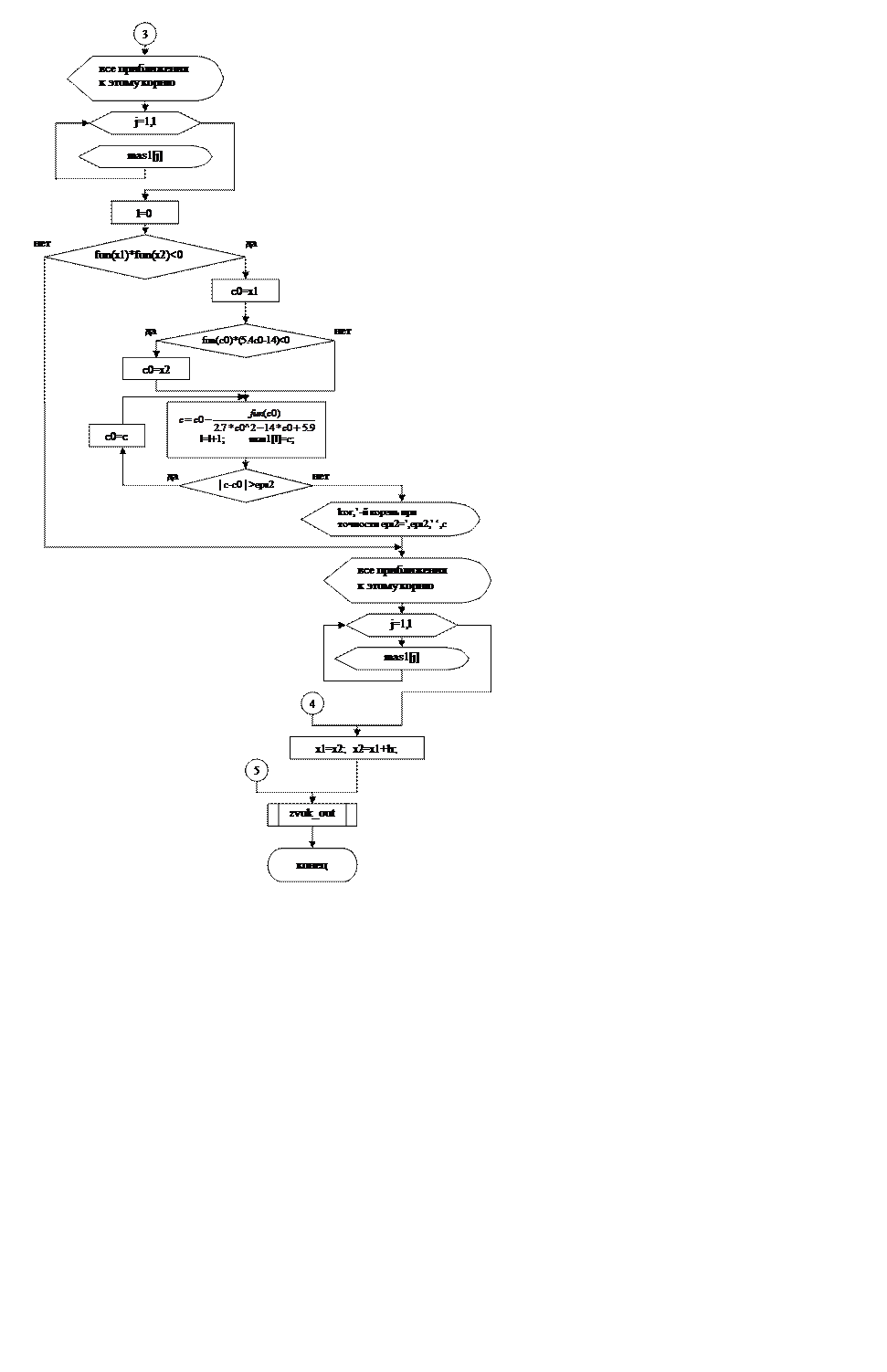
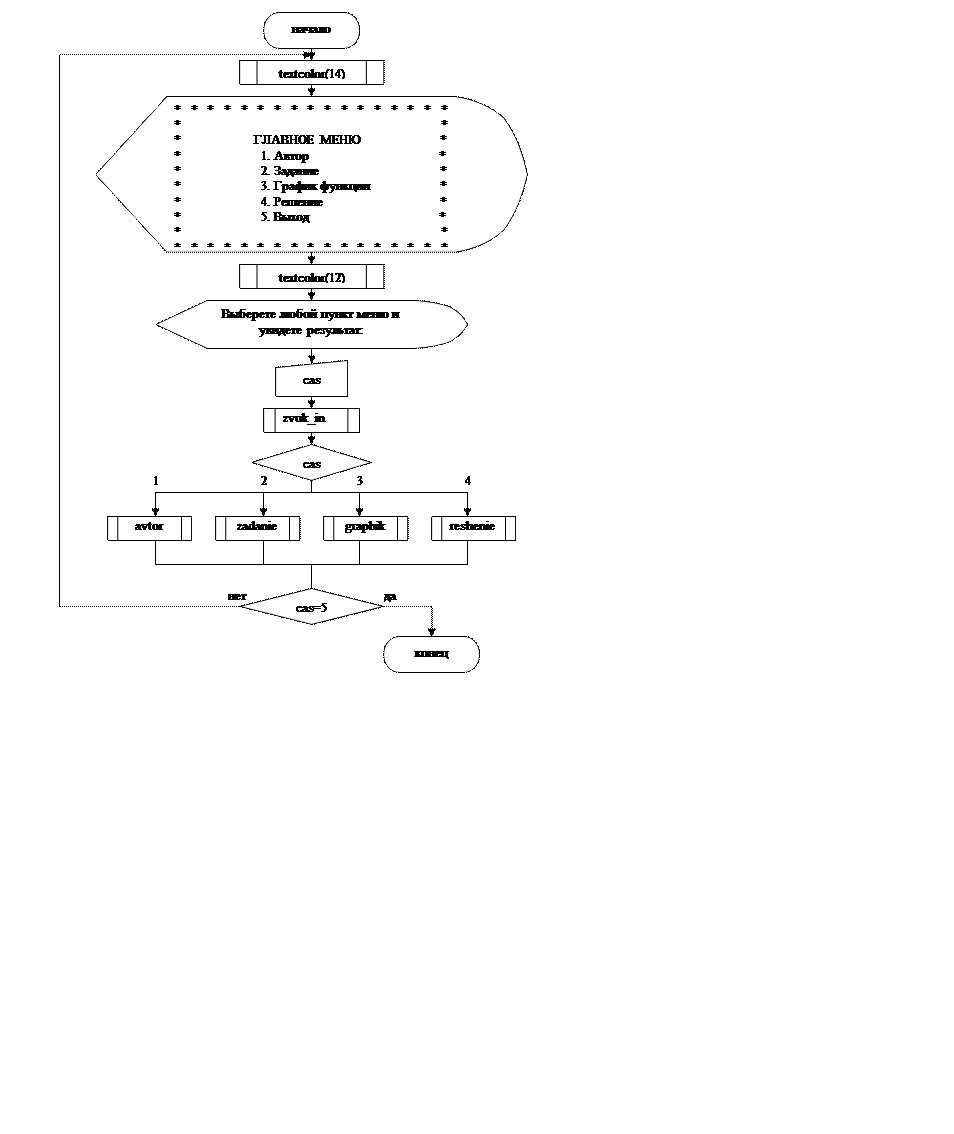
3. Входные и выходные данные
Входные:
Процедура zadanie:
f – файловая переменная
i – счетчик
mas – массив из элементов файла
Процедура graphik:
gd – № драйвера
gm – № режима
g – максимальное значение по оси Ох
v – максимальное значение по оси Оу
pox – половина максимального значения по оси Ох
poy – половина максимального значения по оси Оу
k – разметка цифрами по осям
mx – масштаб по оси Ох
my – масштаб по оси Оу
kx – число пикселей на единичном отрезке по Ох
ky – число пикселей на единичном отрезке по Оу
st – строковая переменная
x – приращение функции
Процедура reshenie:
a, b – границы отрезка
h – шаг табулирования
eps1, eps2 – точности расчета корней
kor – счетчик корней
x1, x2 – границы интервала, который может содержать корень уравнения
y1 – значение функции в точке х1
y2 – значение функции в точке х2
l, j – счетчики
c0 – приближение корня по недостатку
mas1 – массив из приближений к корню
c – корень уравнения
Программа:
cas - № пункта меню
Выходные:
введите границы интервала, шаг табулирования и точность расчета корней
a=-1
b=8
h=1
eps1=0.1
eps2=0.01
1-й корень при точности eps1=0.1000 -0.20497419
все приближения к этому корню
mas1[1]=-0.45575221
mas1[2]=-0.24330517
mas1[3]=-0.20497419
1-й корень при точности eps2=0.0100 -0.20371344
все приближения к этому корню
mas1[1]=-0.45575221
mas1[2]=-0.24330517
mas1[3]=-0.20497419
mas1[4]=-0.20371344
2-й корень при точности eps1=0.1000 1.20786678
все приближения к этому корню
mas1[1]=1.33628319
mas1[2]=1.21508491
mas1[3]=1.20786678
2-й корень при точности eps2=0.0100 1.20786678
все приближения к этому корню
mas1[1]=1.33628319
mas1[2]=1.21508491
mas1[3]=1.20786678
3-й корень при точности eps1=0.1000 6.77372179
все приближения к этому корню
mas1[1]=6.78855721
mas1[2]=6.77372179
3-й корень при точности eps2=0.0100 6.77365054
все приближения к этому корню
mas1[1]=6.78855721
mas1[2]=6.77372179
mas1[3]=6.77365054
Заключение
В результате проделанной работы я составил программу, позволяющую на заданном интервале [a,b] локализовать корни уравнения F(x)=0, найти их с заданной точностью методом касательных (Ньютона), построить график функции. Сопоставив результаты, полученные графическим и аналитическим способами, можно заметить, что они практически совпадают.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.