Вычисление матричных выражений в Excel

Аннотация

Пояснительная записка представляет собой отчет о выполнении расчетно-графического задания на тему: «Вычисление матричных выражений». Расчеты выполнены в Excel двумя способами: с представлением и без представления промежуточных данных.

Матрицы, участвующие в вычислениях подобраны самостоятельно. Отчет составлен с помощью текстового процессора Word.

Оглавление

Введение………………………………………………………………………………..2

1.Теоретические сведения……………………………………………………………..3

2.Задание и анализ матричного выражения………………………………………….4

3.Подготовка теста……………………………………………………………………..4

4.Вычисление матричного выражения……………………………………………….5

   4.1.Вычисление с записью промежуточных матриц………………………………5

   4.2.Вычисление без записи промежуточных матриц……………………………...7

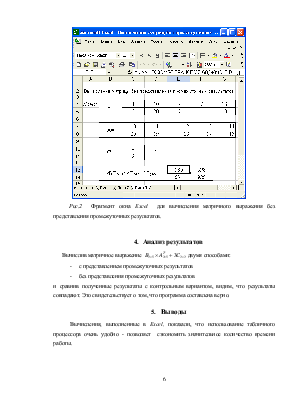
5.Анализ результатов………………………………………………………………….8

6.Выводы……………………………………………………………………………….8

Заключение………………………………………………………………..……………8

Библиографический список……………………………………………………………8

Введение

В инженерно-технической практике часто возникает необходимость в различных вычислениях с помощью матриц. Обычно действия с матрицами используются при решении систем линейных уравнений. Вручную выполнять расчёты неудобно, т. к. это требует больших затрат времени, поэтому выполнять расчёты с матричными выражениями целесообразно с помощью табличного процессора Excel.

Excel содержит специальные функции для действий с матричными выражениями:

МУМНОЖ - для умножения матриц;

МОБР – для вычисления обратной матрицы;

МОПРЕД – для вычисления определителя матрицы;

ТРАНСП – для транспонирования матрицы.

Данные подобраны самостоятельно. Матричные выражения вычислены 2-мя способами:   1) С представлением промежуточных результатов;

          2) Без представления промежуточных результатов.

1.  Теоретические сведения

Прямоугольной матрицей размерности  называется таблица элементов, состоящая из строк и  столбцов.

Матрица, состоящая из одной строки, называется матрицей-строкой.

Матрица, состоящая из одного столбца, называется матрицей-столбцом.

Матрица, в которой количество строк совпадает количеством столбцов, называется    квадратной матрицей

Матрица, в которой все элементы, кроме тех, которые расположены на главной  диагонали, равны «0», называется диагональной матрицей.

Треугольной матрицей называется такая квадратная матрица, все элементы которой, расположенные над (под) главной диагональю, равны «0».

Действия с матрицами.

1)  Сложение. Складываются  матрицы только одинаковой размерности.

2)  Умножение на скаляр. На скаляр можно умножить любую матрицу.

3)  Произведение матриц. Умножение матрицы  А на матрицу  В возможно только в том случае, если число столбцов матрицы А совпадает с числом строк матрицы  В.

 Для этого в Excel существует функция МУМНОЖ.

4)  Транспонирование матриц. Транспонировать можно любую матрицу, при этом строки исходной матрицы становятся столбцами новой, а столбцы – строками.

Для этого в Excel  существует функция ТРАНСП.

5)  Вычисление определителя матриц. Операция производится для любого вида матриц.

Для этого в Excel существует функция МОПРЕД.

6) Вычисление обратной матрицы. Эта операция возможна только в том случае, если определитель не равен «0».

Для этого в Excel существует функция МОБР.

           2.Задание и анализ матричного выражения