Использование современной компьютерной техники и программного обеспечения для решения прикладных задач в области обогащения полезных ископаемых, страница 7

В качестве теста используются результаты ручного счёта. Подставляя в матрицу известные коэффициенты, получаем нужную нам матрицу.

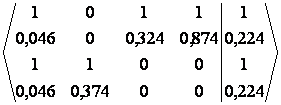
Рис 3. Исходная расширенная матрица

Решение полученной расширенной матрицы с помощью MS-Excel представлено на рисунке 4.

Рис.4. Решение с помощью MS-Excel

В результате ручного счёта получены расчётные долевые выходы продуктов (см. таблицу 2).

Таблица 2

Результаты ручного счёта

Обозначение	Значение
	0,457317
	0,542683
	0,493348
	0,049335

1.6.  Разработка алгоритма решения задачи

В этом пункте приведены:

§  Укрупнённый алгоритм и его описание

§  Детали алгоритма и их описание

1.6.1.  Укрупненный алгоритм и его описание

Для выполнения расчётов следует составить программу, которая обеспечивает выполнение следующих шагов:

§  Ввод и вывод заданных содержаний полезного компонента

§  Формирование массивов, содержащих коэффициенты при неизвестных и свободные члены системы линейных алгебраических уравнений

§  Вызов подпрограммы, реализующей метод Гаусса

§  Вывод результатов

Укрупнённый алгоритм решения задачи представлен на рисунке 5.

 

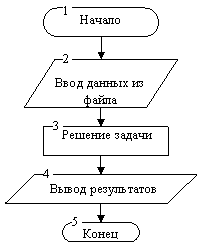
Рис. 5. Укрупнённый алгоритм программы

1.6.2.  Детали алгоритма и их описание

Шаги 1-2 блок-схемы (см. рисунок 5) в комментариях не нуждаются.

Заполнение массива переменных перед неизвестными и столбца свободных членов производиться простым присваиванием определённым ячейкам нужных значений. Алгоритм представлен на рисунке 6.

 

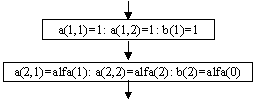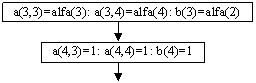Рис. 6. Заполнение массива переменных перед неизвестными

Алгоритм вывода на экран и в файл расширенной матрицы не нуждается в комментариях и расшифровке.

Вызов подпрограммы gauss, выполняющей решение расширенной матрицы по методу Гаусса не требует показа блок-схемы и выглядит следующим образом: