

Задача 1
Пусть один сборщик собирает картофель в ведро с одного рядка и затем высыпает его в мешок.
Требуется оценить величину суммарного расстояния R(Xм), которое нужно пройти сборщику, если мешок располагается в точке рядка с координатой Xм. Считать, что картофель уже извлечен на поверхность рядка.
Указание. Предварительно выполнить статистическое наблюдение для детерминированной ситуации, когда в ведро помещается 10 кг картофеля, в мешок - 4 ведра, а урожайность картофеля составляет 10 кг/пог.м.
Решение
1-й этап.
Статистическое наблюдение дает нам следующую таблицу
Таблица 1
|
Xм |
R(Xм) |
|
0 |
24 |
|
1 |
16 |
|
2 |
12 |
|
3 |
12 |
|
4 |
16 |
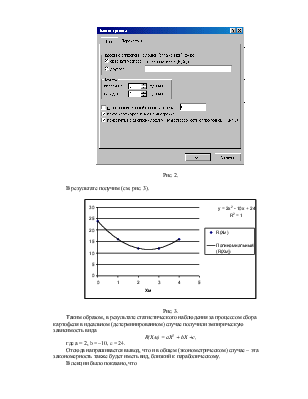
Установим закономерность R(Xм)=F(Xм) графическим способом.
Мастер функций à Точечная à Готово
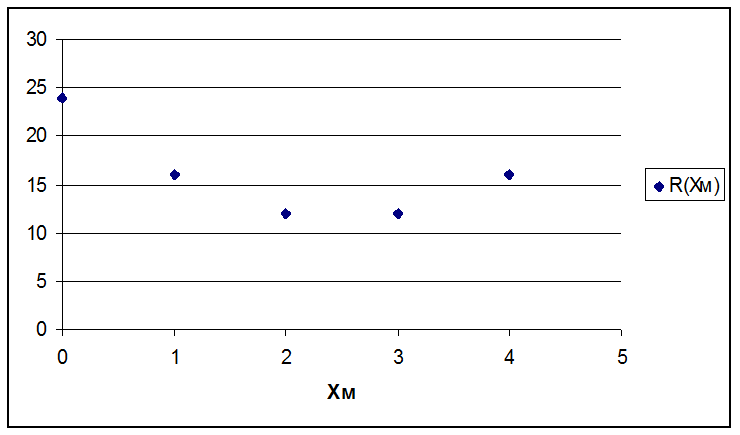
Рис. 1.
1ПМ по эмпирической точке à Добавить линию тренда
Выбрать тип "Полиномиальная" и перейти на вкладку Параметры.
Поставить птички, как показано на рисунке и OK.
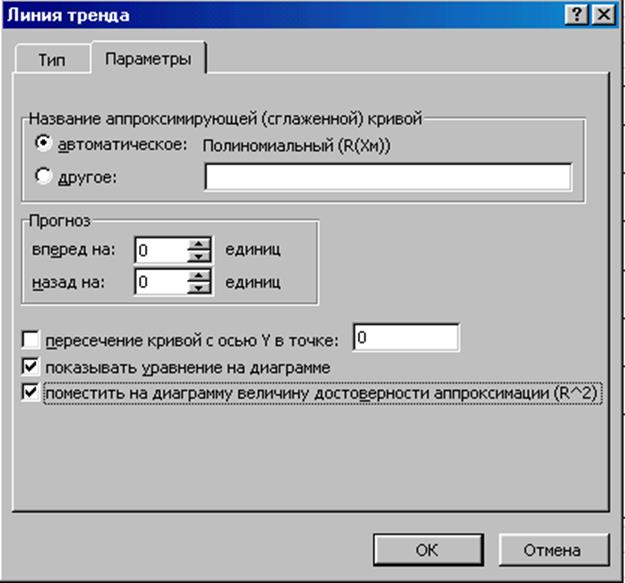
Рис. 2.
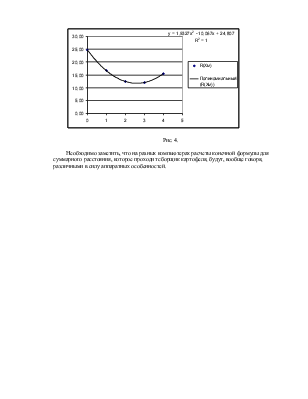
В результате получим (см. рис. 3).
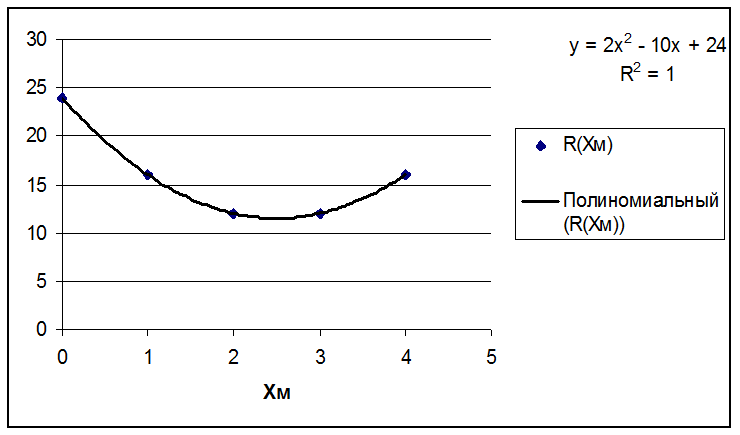
Рис. 3.
Таким образом, в результате статистического наблюдения за процессом сбора картофеля в идеальном (детерминированном) случае получили эмпирическую зависимость вида
R(Xм) = aX2 + bX +c,
где а = 2, b = –10, c = 24.
Отсюда напрашивается вывод, что и в общем (эконометрическом) случае – эта закономерность также будет иметь вид, близкий к параболическому.
В лекции было показано, что
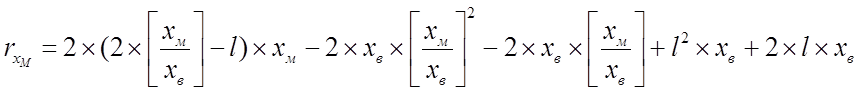 , (1)
, (1)
где Xв – расстояние, которое нужно пройти, чтобы собрать одно ведро картофеля, l – емкость мешка […] – функция целой части числа.
2–й этап.
Считаем теперь урожайность случайной величиной, которая приводит к тому, что модель для Xв приобретает следующий (простейший) вид
![]() ,
,
где ![]() –
случайная величина, равномерно распределенная на отрезке [0, 1].
–
случайная величина, равномерно распределенная на отрезке [0, 1].
Оставляя предположение о емкости мешка l = 4 ведра, и, используя функции Excel СЛЧИС() и ОКРУГЛ(), на основе соотношения (1) построим таблицу, аналогичную таблице 1. Имеем табл. (2)
Таблица 2
|
Xм |
R(Xм) |
|
0 |
25,95 |
|
1 |
17,62 |
|
2 |
12,97 |
|
3 |
12,00 |
|
4 |
14,70 |
В табл. 2 вторая ячейка второго столбца рассчитывается по формуле:
=2*(2*ОКРУГЛ(A28/(1+$F$28);0)-4)*A28-2*(1+$F$28)*ОКРУГЛ(A28/(1+$F$28);0)^2-2*(1+$F$28)*ОКРУГЛ(A28/(1+$F$28);0)+24*(1+$F$28),
где значение равномерно распределенной случайной величины вычисляется в ячейке F28 по формуле =0,1*СЛЧИС(). Значения остальных ячеек второго столбца формируются путем копирования.
В результате имеем (см. рис. 4)
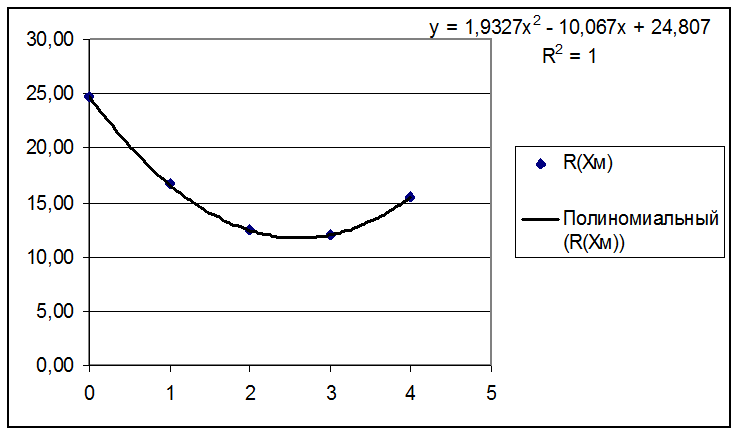
Рис. 4.
Необходимо заметить, что на разных компьютерах расчеты конечной формулы для суммарного расстояния, которое проходит сборщик картофеля, будут, вообще говоря, различными в силу аппаратных особенностей.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.