Индивидуальное задание № 2
Определение перемещений в статически определимой раме (срок 6-12 неделя)
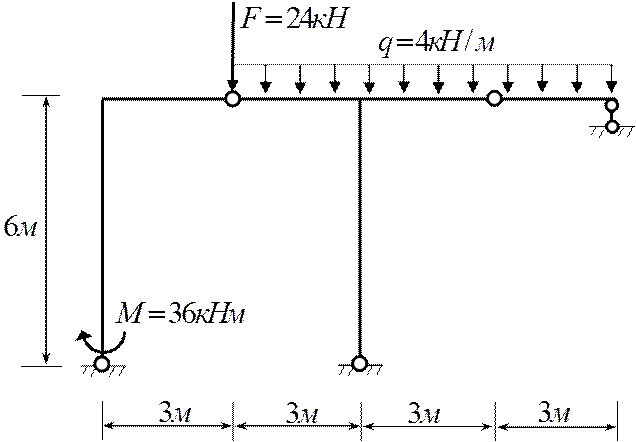
Требуется: 1) построить эпюры
внутренних усилий;
2) найти полное линейное
перемещение замкового
шарнира в главной части
и взаимный угол поворота
сечений примыкающих к шарниру
между второстепенной и
главной частью.
Решение
I. Кинематический анализ системы
1) Количественный анализ
 Необходимое
условие геометрической
Необходимое
условие геометрической
неизменяемости: 3Д-(2Н+С0)≤0
Д=3, Н=2, С0=5
3×3-(2×2+5)=9-9=0
Условие выполняется.
2) Структурный анализ
Три диска (Д0, Д1, Д2) соединяются
тремя шарнирами, не лежащими
на одной прямой. Эти диски
образуют распорную систему.
К этой геометрически неизменяемой
системе шарниром и опорной связью
присоединяется диск Д3
Настоящая рама является геометрически неизменяемой системой, поэтому дальнейший расчет имеет смысл.
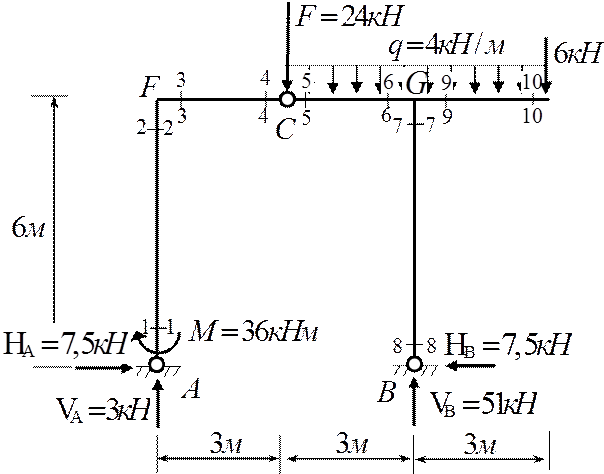
II. Построение эпюр внутренних усилий в раме
1) Рабочая схема рамы
Рабочая схема – это схема взаимодействия главных и второстепенных частей и элементов рамы, показывающая порядок передачи нагрузки. Главная часть это та часть, которая может самостоятельно воспринимать заданную нагрузку. Второстепенная часть это та часть, которая теряет несущую способность, если отбросить соседние части. Она опирается на главную часть.
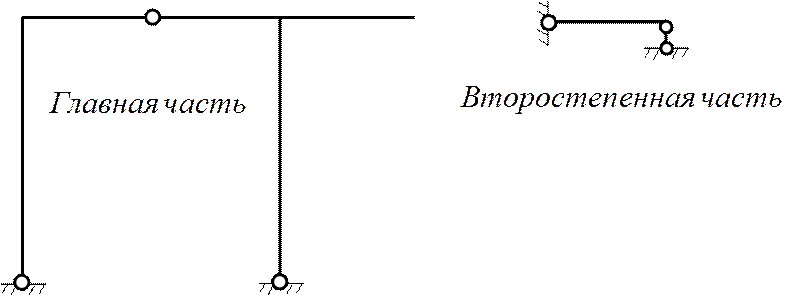 |
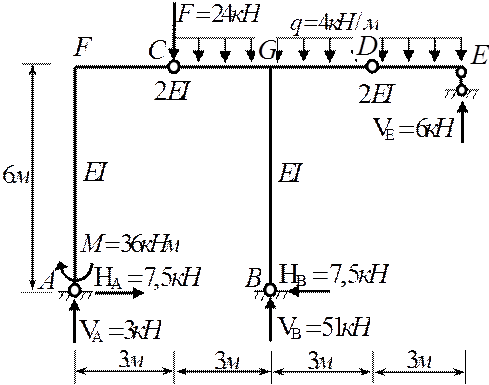
2) Определение опорных реакций
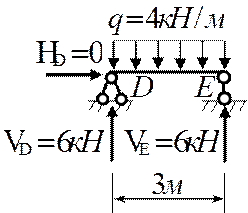 Расчет
производят, начиная с верхнего элемента, воздействие (опорная реакция)
передается от верхнего к нижнему элементу с обратным знаком (третий закон
Ньютона).
Расчет
производят, начиная с верхнего элемента, воздействие (опорная реакция)
передается от верхнего к нижнему элементу с обратным знаком (третий закон
Ньютона).
Определение опорных
реакций во второстепенной
части (простая балка со
стандартной нагрузкой):
∑Fy=0 => VD=VE=ql/2=6кН
Определение опорных реакций
 в главной
части рамы:
в главной
части рамы:
∑mA=0; M+3F+6×6q-6VВ+9×6=0
6VВ=36+72+144+54
VВ=51кН
∑mВ=0; M+3×6+6VА-3F-6q×0=0
6VА=-36-18+72
VА=3кН
Проверка: ∑Fy=0; 3+51-24-6×4-6=0
54-54=0
0=0 верно.
∑mСлев=0; М+3VА-6НА=0
6НА=36+3×3
НА=7,5кН
∑mСпр=0; 3×6q+6×6+6НВ-3VВ=0
6НВ=-72-36+153
НВ=7,5кН
Проверка: ∑Fx=0; НА-НВ=0
7,5-7,5=0
0=0 верно.
3)
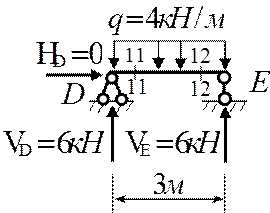 Построение эпюр N, Q и M
Построение эпюр N, Q и M
Первой строят эпюру изгибающих моментов
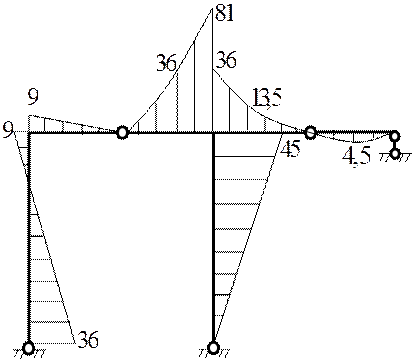
Эпюра М [кНм]
Проверка правильности построения эпюры моментов
 выполняется
методом вырезания узлов.
выполняется
методом вырезания узлов.
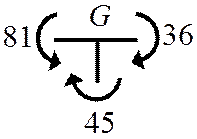 |
|||
 |
|||
Очевидно, что оба узла находятся в равновесии
Эпюру поперечных сил строят по эпюре моментов,
используя два подхода. Во-первых, значения поперечной силы на грузовых участках
находят как первую производную от функции моментов 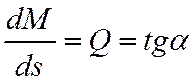 .
Во-вторых, значения поперечной силы на грузовых участках можно определить,
рассматривая равновесие элемента (из уравнений статики).
.
Во-вторых, значения поперечной силы на грузовых участках можно определить,
рассматривая равновесие элемента (из уравнений статики).
 На
эпюре моментов представлены величины угла α, определив значения tgα,
получим значения поперечной силы на соответствующих грузовых участках (I, II, IV).
На
эпюре моментов представлены величины угла α, определив значения tgα,
получим значения поперечной силы на соответствующих грузовых участках (I, II, IV).
QI= tgαI=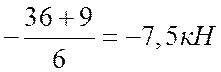
QII= tgαII=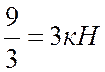
QIV= tgαIV=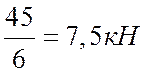
На третьем и пятом грузовых
участках значение поперечной силы
можно определить, рассматривая
равновесие элемента.
Третий грузовой участок
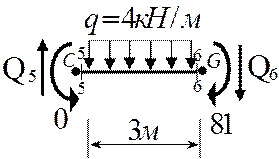 ∑mС=0; 3Q6+1,5×3q+M=0
∑mС=0; 3Q6+1,5×3q+M=0
3Q6+1,5×3×4+81=0
Q6=-33кН
∑mG=0; 3Q5-1,5×3q+M=0
3Q5-1,5×3×4+81=0
Q5=-21кН
Проверка: ∑Fy=0; Q5-Q6-3×4=0
-21+33-12=0
33-33=0
Пятый грузовой участок 0=0 верно.
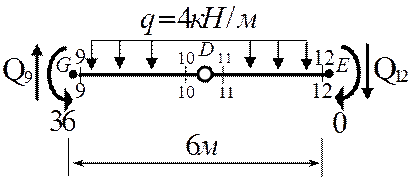
Эпюра Q[кН]
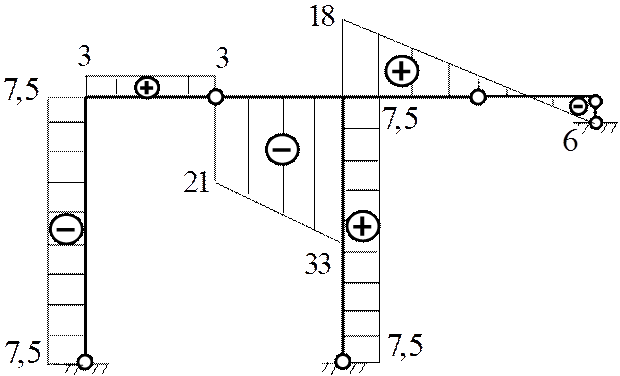 |
∑mG=0; 6Q12+3×6q-M=0
6Q12+3×6×4-36=0
Q12=-6кН
∑mЕ=0; 6Q9-3×6q-M=0
6Q9-3×6×4-36=0
Q9=18кН
Проверка: ∑Fy=0; Q9-Q12-6×4=0
18+6-24=0
24-24=0
0=0 верно.
Для построения эпюры продольных сил используют метод вырезания узлов. С эпюры поперечных сил в узел выставляют значения внутренних усилий и уравновешивают их значениями продольной силы.
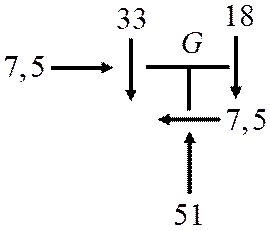 |
|||
 |
|||
Эпюра N[кН]
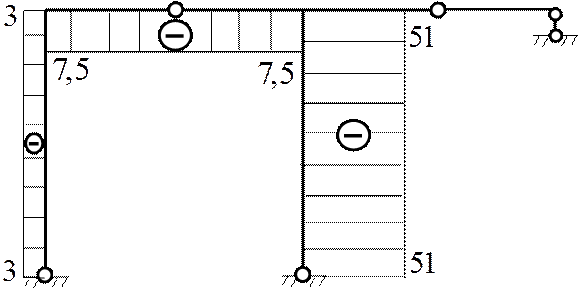 |
Проверка равновесия отсеченной части (ригеля).
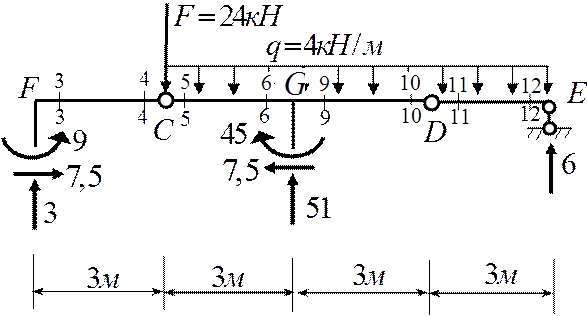 |
∑Fx=0; -7,5+7,5=0
∑Fy=0; 3+51+6+-24-4×9=60-60=0
∑mСлев=0; 3×3-9=9-9=0
∑mСпр=0; 4×9×4,5-6×9+45-51×3=207-207=0
∑mDпр=0; -6×3+4×3×1,5=-18+18=0
Окончательно результаты построения эпюр представляют в следующем виде.

III. Определение перемещений
 При
жесткости EI=10000кНм2 требуется определить
вертикальное vC и
горизонтальное uC перемещения точки С, а также взаимный угол поворота θD точки D. Соотношение жесткостей на грузовых участках задают
после определения перемещений из условий жесткости.
При
жесткости EI=10000кНм2 требуется определить
вертикальное vC и
горизонтальное uC перемещения точки С, а также взаимный угол поворота θD точки D. Соотношение жесткостей на грузовых участках задают
после определения перемещений из условий жесткости.
1)
![]()
 Построение грузовой эпюры моментов (выполнено ранее)
Построение грузовой эпюры моментов (выполнено ранее)
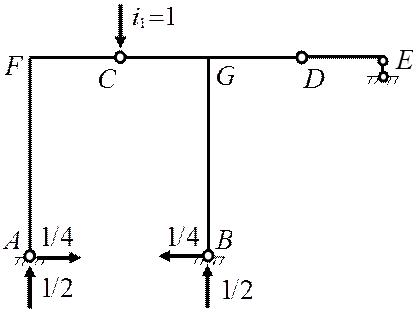
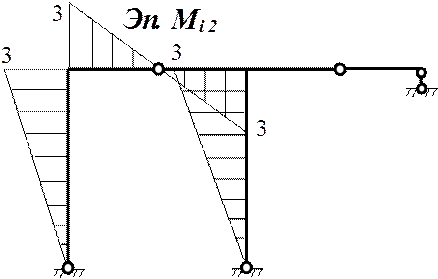
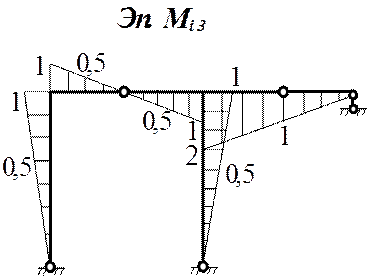
![]() 2) Построение эпюр моментов от единичных силовых
воздействий, соответствующих определяемым перемещениям
2) Построение эпюр моментов от единичных силовых
воздействий, соответствующих определяемым перемещениям
 |
|||||||
 |
|||||||
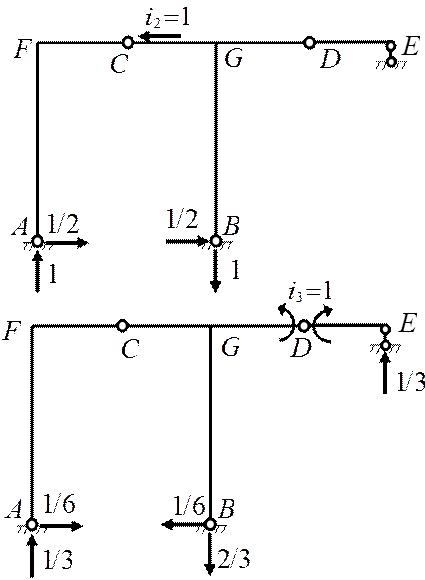 |
|||||||
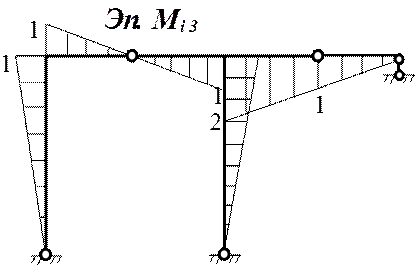 |
|||||||
Перемещения (∆iF) находят как сумму интегралов от произведения функций изгибающих моментов, вызванных нагрузками и единичными силовыми воздействиями (i1, i2, i3), отнесенного к жесткости (EI). Для сопряжения эпюр можно использовать формулу Симпсона и правило Верещагина (оба способа рассмотрены в курсе лекций). В настоящей работе применяется формула Симпсона, полученная для приближенного вычисления интеграла от произведения двух функций, заданных графически (в контексте примера речь идет об эпюрах изгибающих моментов). В рассматриваемой задаче график функции на грузовых участках это прямые линии либо параболы, а в таком случае формула Симпсона дает точное значение интеграла. Перемещения находят как
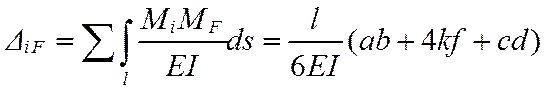 ,
,
где ![]() - функция изгибающих моментов от единичного силового
воздействия,
- функция изгибающих моментов от единичного силового
воздействия, ![]() - функция изгибающих моментов от нагрузок,
- функция изгибающих моментов от нагрузок, ![]() -
длина грузового участка,
-
длина грузового участка, ![]() - жесткость,
- жесткость, ![]() - приведены ниже на рисунке.
- приведены ниже на рисунке.
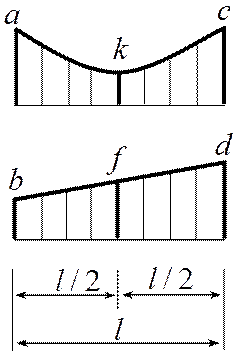
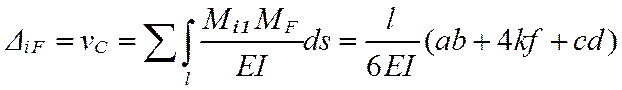
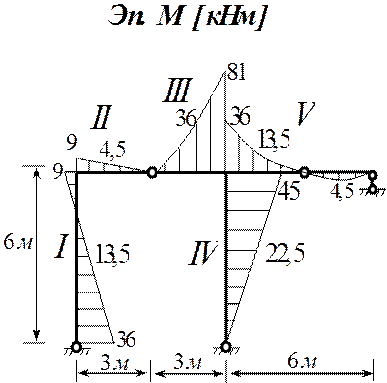 |
|||||
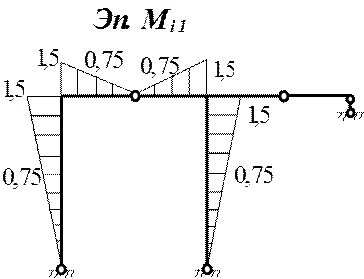 |
|||||
 |
|||||
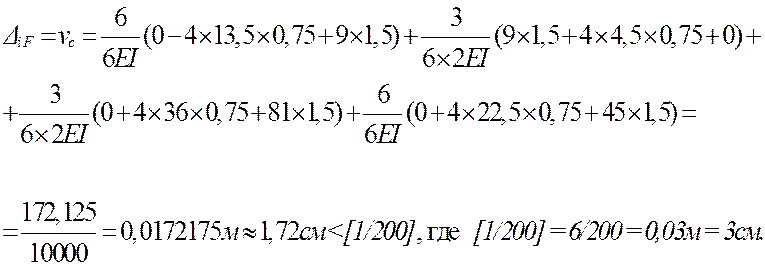
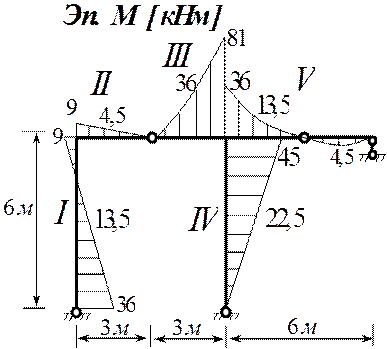 |
|||
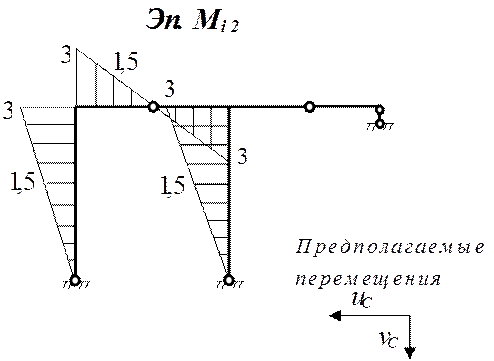 |
|||
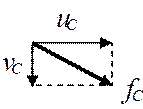
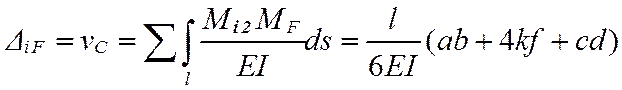
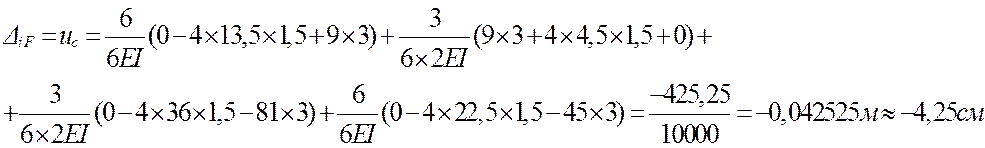
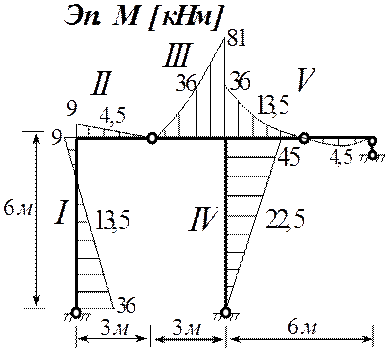 |
|||
 |
|||
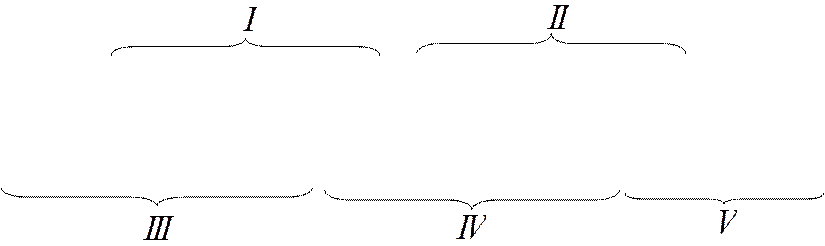
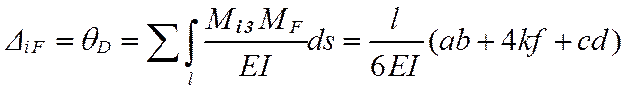
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.