Индивидуальное задание № 3
Расчет статически неопределимой рамы методом сил (срок 11-15 неделя)

Требуется:
1) построить эпюры внутренних усилий;
2) найти опорные реакции.
Соотношение жесткостей ![]()
в стойках и ригеле (1:2).
Решение
1) Определим степень статической неопределимости
Степень статической неопределимости находят с помощью формулы nst=3K-H, где K – количество замкнутых контуров системы, H – число простых шарниров.
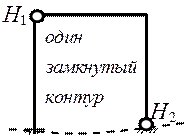
nst=3K-H=3×1-2=1 - задача один раз статически неопределимая.
Для раскрытия статической неопределимости
воспользуемся методом сил.
2) Рассмотрим возможные варианты основных систем метода сил
Основной системой метода сил (ОСМС) называют систему, образованную из заданной удалением лишних связей, если удалить все лишние связи, то ОСМС будет статически определимой системой. Усилия в лишних связях обозначают x1 (неизвестные метода сил). Это продемонстрировано ниже.
 |
|||||||
 |
|||||||
 |
|||||||
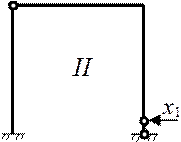 |
|||||||
Кинематический
анализ систем
На рисунке приведены два из возможных вариантов ОСМС, оба варианта являются геометрически неизменяемыми системами. К расчету примем первый вариант ОСМС.
3) Определение неизвестного (x1) метода сил
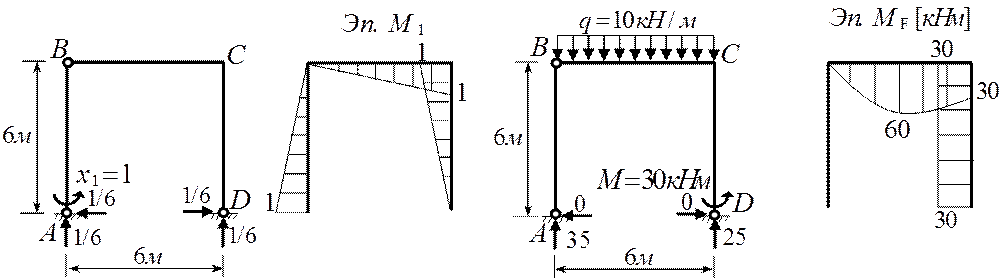 Для
первого варианта ОСМС построим эпюры моментов от неизвестного x1=1 и
нагрузки, предварительно определив опорные реакции.
Для
первого варианта ОСМС построим эпюры моментов от неизвестного x1=1 и
нагрузки, предварительно определив опорные реакции.
В заданной системе в точке А (жесткая заделка) поворот
невозможен. Перемещение (угол поворота) в точке А по направлению неизвестного x1
от действия заданной нагрузки в ОСМС ![]() =0 (это условие
неразрывности перемещений). Угол поворота сечения в точке А (по направлению x1
от действия заданной нагрузки) в заданной системе равен углу поворота в ОСМС и
равен нулю. Развернутая форма условия неразрывности перемещений имеет вид
=0 (это условие
неразрывности перемещений). Угол поворота сечения в точке А (по направлению x1
от действия заданной нагрузки) в заданной системе равен углу поворота в ОСМС и
равен нулю. Развернутая форма условия неразрывности перемещений имеет вид ![]() (отрицание перемещения по
направлению неизвестного x1).
(отрицание перемещения по
направлению неизвестного x1).
Для сопряжения эпюр в настоящей работе применяется формула Симпсона, полученная для приближенного вычисления интеграла от произведения двух функций, заданных графически (в контексте примера речь идет об эпюрах изгибающих моментов). В рассматриваемой задаче график функции на грузовых участках это прямые линии либо параболы, а в таком случае формула Симпсона дает точное значение интеграла.
Перемещение по направлению неизвестного x1 от самого x1 в ОСМС находят как
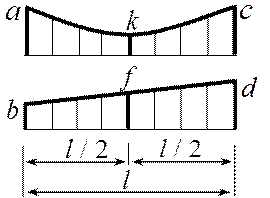
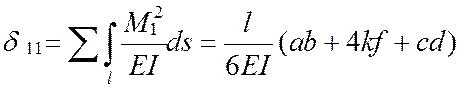 , перемещение по
, перемещение по
направлению неизвестного x1 от действия заданной
нагрузки в ОСМС находят как
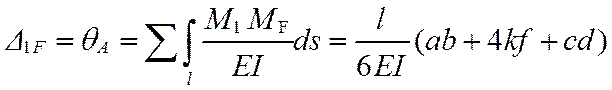 ,
,
где ![]() - функция изгибающих моментов от x1=1,
- функция изгибающих моментов от x1=1, ![]() - функция
изгибающих моментов от заданной нагрузки,
- функция
изгибающих моментов от заданной нагрузки, ![]() - длина грузового участка,
- длина грузового участка, ![]() -
жесткость,
-
жесткость, ![]() - приведены на рисунке справа.
- приведены на рисунке справа.
Перемещение δ11 по направлению x1 от самого x1 в ОСМС находят
путём сопряжения эпюр моментов от x1=1. При расчете необходимо
помнить соотношение жесткостей ![]() в стойках и ригеле (1:2).
в стойках и ригеле (1:2).
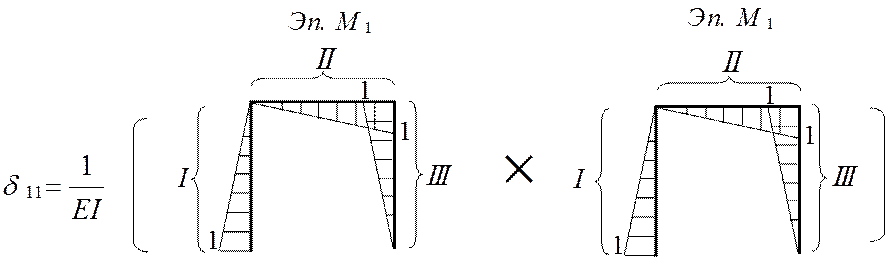
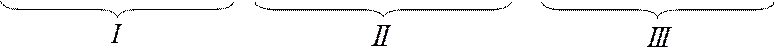
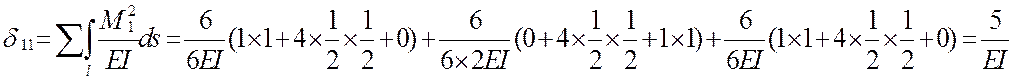
Перемещение по направлению неизвестного x1 от действия заданной нагрузки в ОСМС находят перемножением эпюры моментов от x1=1 и эпюры моментов от заданной нагрузки.
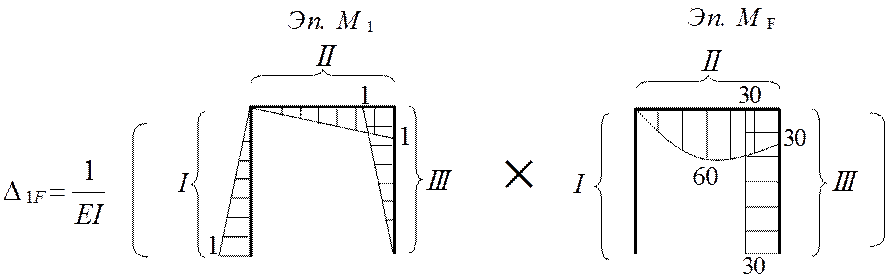 |
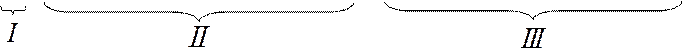
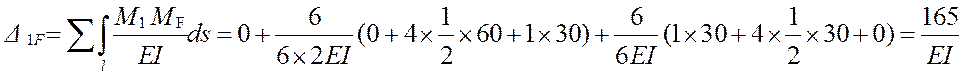
Неизвестное метода сил x1 найдем из условия равенства нулю перемещения по направлению x1 в ОСМС вызванных действием этого неизвестного и нагрузкой.
![]()
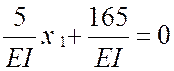
![]()
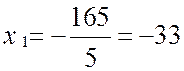
![]() Знак
«-» указывает на то, что усилие x1 ( ) направлено в другую
сторону x1 ( ).
Знак
«-» указывает на то, что усилие x1 ( ) направлено в другую
сторону x1 ( ).
После выполненных операций одна из неизвестных опорных реакций определена МА=-x1=33кНм. Статическая неопределимость раскрыта, можно приступить к построению эпюр внутренних усилий.
4) Построение эпюр внутренних усилий
Эпюра изгибающих моментов
Можно построить эпюру моментов, не определяя опорные реакции, для этого воспользуемся принципом суперпозиции: Мок=М1x1+МF. Предварительно получим эпюру М1x1 при x1=-33.
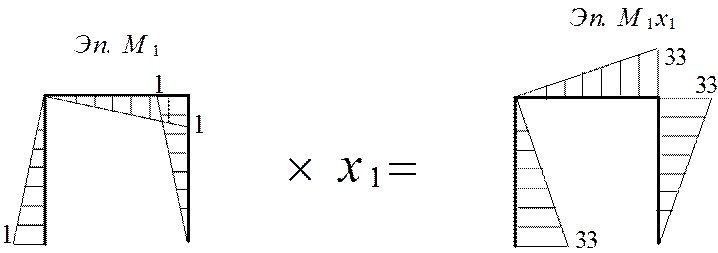 |
Применим принцип суперпозиции.
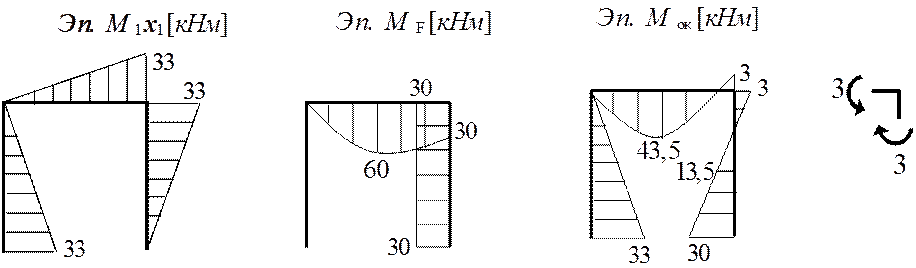 |
+ =
Кинематическая проверка: ![]() =0,
=0,
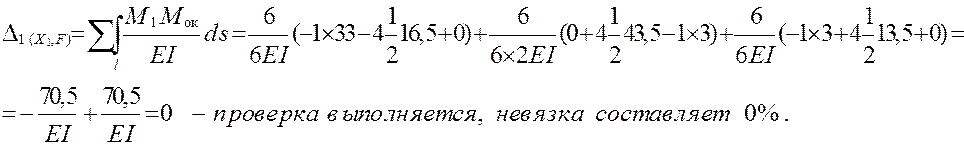
Эпюра поперечных сил
Эпюру поперечных сил строят, опираясь на эпюру
моментов. Значения поперечной силы на грузовых участках находят как первую
производную от функции моментов 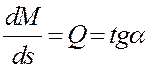 . На грузовых
участках, в пределах которых действует равномерно распределенная нагрузка,
значение поперечной силы определяют, рассматривая равновесие элемента (из
уравнений статики).
. На грузовых
участках, в пределах которых действует равномерно распределенная нагрузка,
значение поперечной силы определяют, рассматривая равновесие элемента (из
уравнений статики).
На эпюре моментов представлены величины угла α, определив значения tgα, получим значения поперечной силы на I и III грузовых участках.
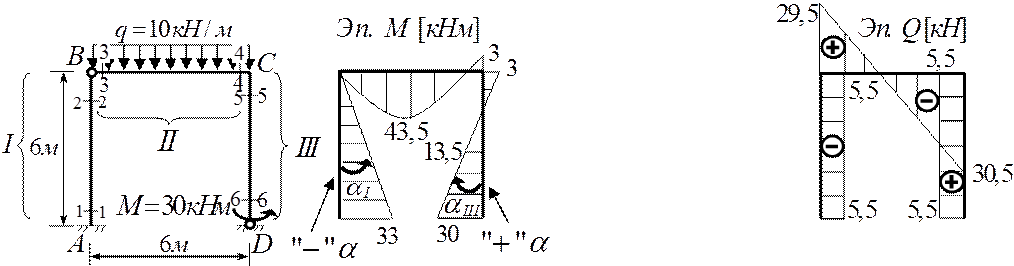
QI= tgαI=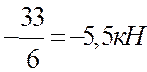
QIII= tgαIII=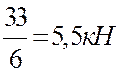
∑mС=0; -6Q3+3×6q-3=0
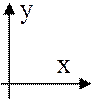
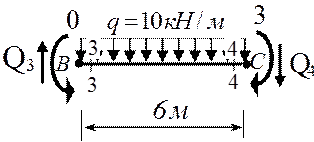 -6Q3+3×6×10-3=0
-6Q3+3×6×10-3=0
Q3=29,5кН
∑mВ=0; 6Q4+3×10q+3=0
6Q4+3×6×10+3=0
Q4=-30,5кН
Проверка: ∑Fy=0; Q3-Q4-6×10=0
29,5+30,5-60=0
60-60=0
0=0 верно.
Эпюра продольных сил
Для построения эпюры продольных сил используют метод вырезания узлов. С эпюры поперечных сил в узел выставляют значения внутренних усилий и уравновешивают их значениями продольной силы.
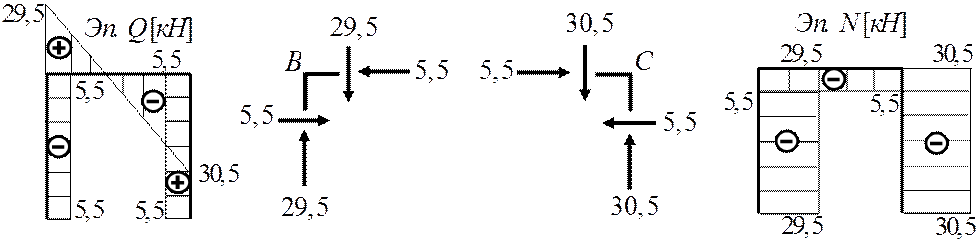
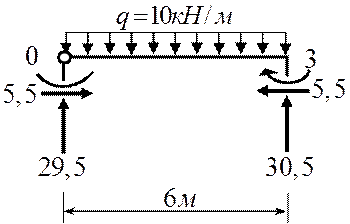 Проверка равновесия ригеля
Проверка равновесия ригеля
∑Fx=0; -7,5+7,5=0
∑Fy=0; 3+51+6+-24-4×9=60-60=0
∑mСлев=0; 3×3-9=9-9=0
∑mСпр=0; 4×9×4,5-6×9+45-51×3=207-207=0
∑mDпр=0; -6×3+4×3×1,5=-18+18=0
Определение опорных реакций по эпюрам внутренних усилий
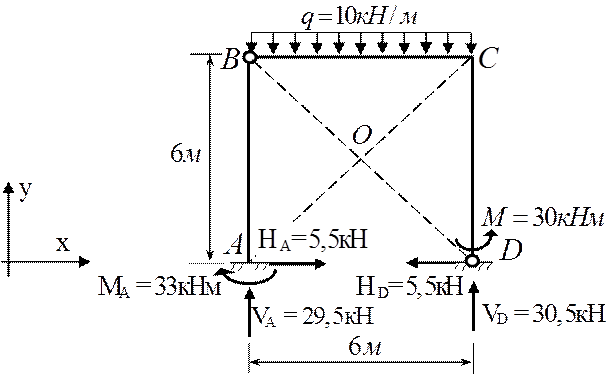
Проверка равновесия системы
∑Fx=0; 5,5-5,5=0
∑Fy=0; 29,5+30,5-10×6=60-60=0
∑mо=0; 10×6×0+5,5×3+33+29,5×3-30-30,5×3-5,5×3=138-138=0
Система находится в равновесии.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.