5.1 Схема алгоритма решения задачи
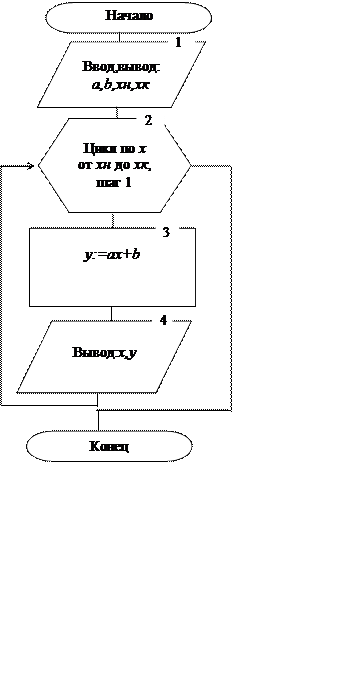 c
c
Программа для решения задачи
program forp;
var
a,b,y:real;
x,xn,xk:integer;
begin
write('введите значения переменных a,b,xn,xk: ');
readln(a,b,xn,xk);
writeln('Исходныеданные: a=',a:4:2,' b=',b:4:2,' xn=',xn,' xk=',xk);
writeln('Результат табулирования функции y=ax+b: ');
for x:=xn to xk do
begin
y:=a*x+b;
writeln(' x=',x,' y=':20,y:4:2);
end;
readln
end.
Лекция 6
Разработка и программирование итерационных алгоритмов
Рассмотрение будет вестись на примере решения конкретных задач.
Задача 1 на использование итерационных алгоритмов
1 Условие задачи
Даны действительные числа a, b и натуральное число n.
Вычислить 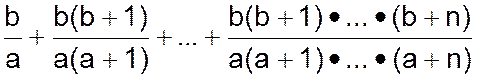
2 Анализ особенностей задачи
В этой задаче удобно считать последнее слагаемое n-ым. С учетом этого, получим заданное выражение в виде:
 |
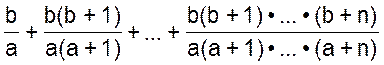
Будем использовать следующие обозначения: Slо, Sl1, …, Sln – соответственно слагаемые нулевое, первое, …, n-oe; So, S1, …, Sn – сумма нулевая, первая, …, n-ая.
Для выполнения циклических действий введем переменную i, которая представляет собой одновременно порядковый номер текущих слагаемого и частичной суммы. Для удобства записи данного выражения с включением в него (i-1) и i-го слагаемых, пусть n достаточно велико, по крайней мере, не меньше пяти, тогда выражение можно записать в виде:
 |
|
|
![]()
|
Из приведенного выражения видно следующее.
Переменная i меняется от нуля до n, с шагом 1.
Для нахождения значения заданного выражения можно использовать циклический алгоритм, в теле цикла которого очередная (текущая) сумма находится в результате сложения предыдущей суммы и текущего слагаемого.
В свою очередь текущее слагаемое находится как произведение предыдущего (i-1)-го слагаемого на сомножитель (b+i)/(a+i).
Решение задачи имеет итерационный характер. Итеративно изменяемыми элементами являются текущие сумма и слагаемое.
При n=1 выражение (полная сумма) вычисляется следующим образом: S1=S0+Sl1, где S0=b/a; Sl1=Sl0·(b+1)/(a+1).
3 Метод решения задачи
С учетом проведенного анализа особенностей задачи, будем использовать для ее решения итерационный алгоритм. Составим два варианта эквивалентных формул, позволяющих найти искомый результат. При первом будем использовать индексированные переменные (массивы). При втором – простые переменные и оператор присваивания. Получим формулы:
Sli=Sli-1·(b+i)/(a+i); Sl:=Sl·(b+i)/(a+i);
Si=Si-1+Sli; S:=S+Sl.
В этом пункте необходимо уточнить пределы изменения i в указанных формулах. Формулы позволяют находить значения текущих слагаемого и суммы по значениям полученным на предыдущем шаге. Но какие-то значения нужно задать в явном виде либо Sl0 и S0, либо Sl1 и S1. В первом случае i=0,…,n, с шагом 1. Это позволяет найти решение при n³0, т.е. и при n=0. А во втором i=1, …,n, т.е. решение можно найти только для натурального n. Далее рассмотрим второй случай. Тогда в приведенных выше формулах i=2,…,n.
![]()
![]() Теперь Sl1=b·(b+1)/[a(a+1)],
при i=1, Sl=b·(b+1)/[a(a+1)]
Теперь Sl1=b·(b+1)/[a(a+1)],
при i=1, Sl=b·(b+1)/[a(a+1)]
S1=a/b+Sl1. S=a/b+Sl.
4 Проверка разработанного метода решения
Она заключается в нахождении и анализе результатов полученных при n=1,2,3 с использованием приведенных в п. 1.3 формул. Здесь и ниже при проверке алгоритма, результаты могут фиксироваться, как в численном виде, так и в общем.
5 Блок-схема алгоритма решения задачи с использованием индексированных переменных
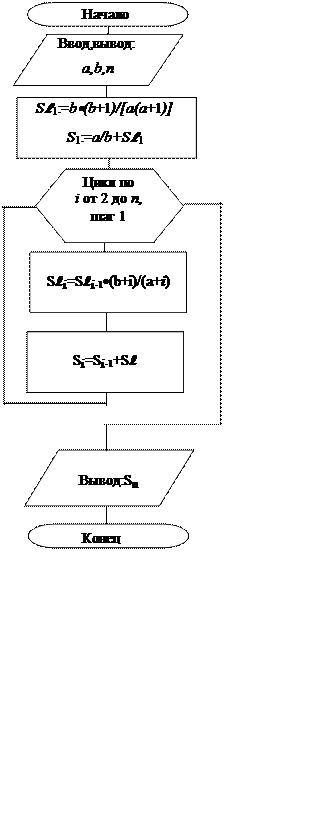 |
6 Блок-схема алгоритма решения задачи без использования индексированных переменных
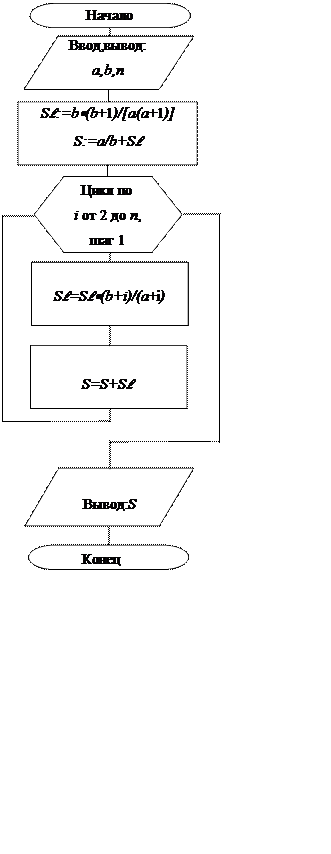 |
7 Протокол испытания алгоритма
Необходимо осуществить пошаговое выполнение алгоритма с фиксацией результатов испытания, которые затем будут использованы при отладке программы. При наличии в алгоритме ошибок и удачном выборе тестовых наборов ошибки будут обнаружены уже на стадии составления алгоритма.
8 Программа для решения задачи без использования индексированных переменных
program Iter;
var a,b,s,sl:real; i,n:integer;
begin
write('введитезначенияпеременных a,b,n: '); readln(a,b,n); writeln('Исходныеданные: a=',a:4:2,' b=',b:4:2,' n=',n); sl:=b*(b+1)/(a*(a+1));
s:=b/a+sl;
for i:=2 to n do
begin
sl:=sl*(b+i)/(a+i);
s:=s+sl
end;
writeln('Результат: выражение равно ',s:4:2);
readln
end.
Задача 2 на использование итерационных алгоритмов
1 Условие задачи
Найти 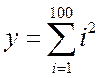
![]()
2 Анализ особенностей решения задачи
Из формулы видно, что требуется найти сумму слагаемых. Их порядковые номера принимают значения от 1 до 100 с шагом 1, т.е. требуется найти сумму ста слагаемых. Для упрощения анализа правильности работы алгоритма и расширения сферы применения программы (нахождения суммы произвольного количества слагаемых) целесообразно максимальный порядковый номер слагаемого 100 заменить на n .
Текущее (i-е) слагаемое находится по формуле: Sli=i2. Каждое слагаемое, в отличие от предыдущей задачи, не является итеративно изменяемым элементом, т. к. значение текущего слагаемого не зависит от значения предшествующего слагаемого.
Можно записать, что у=Sn, где Sn - n-я сумма. Пусть n=3. Тогда имеет место следующее равенство: у=Sl1 + Sl2 + Sl3. Текущая сумма Si является итеративно изменяемым элементом, например, S3=S2+ Sl3. В этой задаче в качестве явно получаемого значения текущей суммы S1 возьмем 11=1.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.