Петербургский Государственный Университет
Путей Сообщения
Кафедра физики.
Лаборатория молекулярной физики.
Лабораторная работа №116.
Определение модуля сдвига методом крутильных колебаний.
|
Работу выполнил студент группы ЭС-404 |
Работу проверил |
|
Ильинский Андрей Станиславович |
Санкт-Петербург
2004
Цель работы: определение модуля сдвига материала проволоки методом крутильных колебаний.
Сведения из теории:
Определение модуля сдвига методом крутильных колебаний.
Рассмотрим
круглый цилиндр длиной L и
диаметром d, у которого
верхнее сечение неподвижно закреплено, а к нижнему приложен момент силы M, который осуществляет закручивание
цилиндра. При таком закручивании нижний конец цилиндра поворачивается на угол ![]() . В пределах упругой деформации
величина
. В пределах упругой деформации
величина ![]() , т.е. относительная деформация
цилиндра пропорциональна закручивающему моменту:
, т.е. относительная деформация
цилиндра пропорциональна закручивающему моменту:
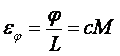 (1)
(1)
Где c – постоянная для данного цилиндра величина, зависящая от его диаметра d и модуля сдвига N.
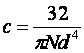 (2)
(2)
Таким образом,
угол закручивания ![]() зависит от модуля сдвига и
обратно пропорционален диаметру стержня, взятому в четвертой степени. Если уравнение (1) переписать в виде:
зависит от модуля сдвига и
обратно пропорционален диаметру стержня, взятому в четвертой степени. Если уравнение (1) переписать в виде:
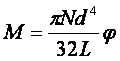 (3)
(3)
То видно, что
момент силы, обеспечивающий закручивание цилиндра на угол ![]() тем меньше, чем больше длина
цилиндра и меньше его диаметр. Величина
тем меньше, чем больше длина
цилиндра и меньше его диаметр. Величина
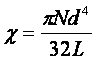 (4)
(4)
обычно называется модулем кручения.
Рассмотрим собственные крутильные колебания тела с моментом инерции J, подвешенного на тонкой нити. Нить можно рассматривать как цилиндр малого диаметра d и длиной L. Момент инерции самой нити можно считать бесконечно малым.
Согласно основному закону динамики вращательного движения тела, имеем:
![]() (5)
(5)
Где – M момент
сил, приложенных к телу;![]() - угловое
ускорение движущегося тела. С другой стороны, угловое ускорение равно второй
производной от угла поворота по времени
- угловое
ускорение движущегося тела. С другой стороны, угловое ускорение равно второй
производной от угла поворота по времени 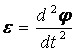 ,
а момент сил, приложенных к телу, равен моменту, приложенному к нити, но имеет
обратное направление.
,
а момент сил, приложенных к телу, равен моменту, приложенному к нити, но имеет
обратное направление.
![]() (6)
(6)
Подставив значения ![]() и M, получим:
и M, получим:
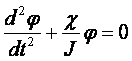 (7)
(7)
Решение этого дифференциального уравнения описывает гармонические колебания
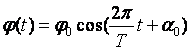 (8)
(8)
где![]() –
амплитуда колебания;
–
амплитуда колебания; ![]() - начальная фаза; T- период колебаний.
- начальная фаза; T- период колебаний.
Таким образом период крутильных колебаний тела, подвешенного на нити, определяется его моментом инерции и модулем кручения нити. Из формул (8) и (4) следует формула для расчета модуля сдвига:
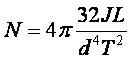
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.