Решение задач целочисленного линейного программирования на ЭВМ

Министерство образования и науки Российской Федерации

Новосибирский государственный технический университет

Кафедра экономической информатики

Отчет

по лабораторной работе №3

«Целочисленное линейное программирование»

Вариант №5

Факультет: Бизнеса

Группа:

Студентка:

Преподаватель: Кириллов Ю.В.

Новосибирск

2007

Цель работы: Приобрести практические навыки и опыт решения задач целочисленного линейного программирования на ЭВМ. Различать общие и частные модели ЗЦЛП, выбирать методы решения, анализировать результаты.

Условие задачи: Коммерческая фирма закупила товары четырех наименований А₁, А₂, А₃, А₄ по 10 упаковок каждого за пределами своего города. Доставку товаров предполагается осуществить собственным автофургоном за несколько рейсов. Грузоподъемность фургона составляет V кг. Вес одной упаковки товара каждого наименования равен соответственно v₁, v₂, v₃, v₄ кг, а стоимость – с₁, с₂, с₃, с₄ тыс. руб.

Определить, какие виды товаров и в каком количестве необходимо перевезти первым рейсом, с тем, чтобы их стоимость была максимальной.

Исходные данные:

V	V1	V2	V3	V4	C1	C2	C3	C4
85	7	14	13	15	15	48	33	50

Порядок выполнения лабораторной работы.

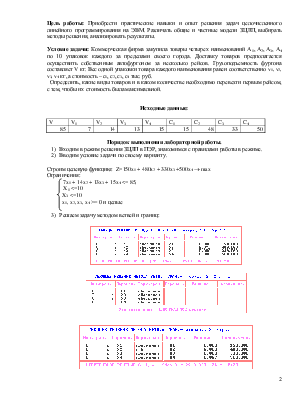
1)  Входим в режим решения ЗЦЛП в ПЭР, знакомимся с правилами работы в режиме.

2)  Вводим условие задачи по своему варианту.

Строим целевую функцию:  Z=150x₁ + 480x₂ + 330x₃ +500x₄ ® max

Ограничения:

            7x₁ + 14x₂ + 13x₃ + 15x₄ <= 85,

            X₁ <=10

           X₃ <=10

           x₁, x₂, x₃, x₄ >= 0 и целые

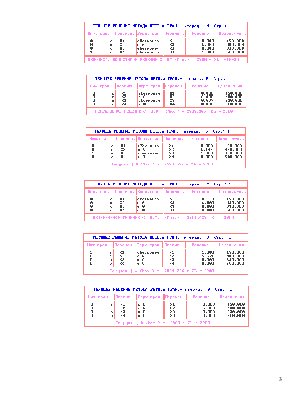
3)  Решаем задачу методом ветвей и границ:

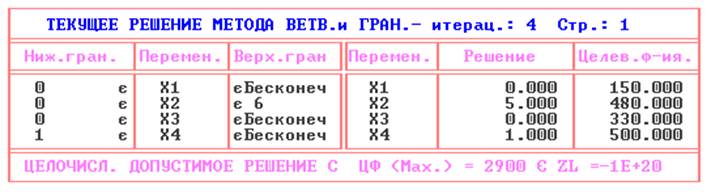
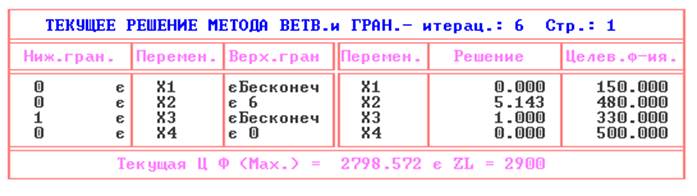
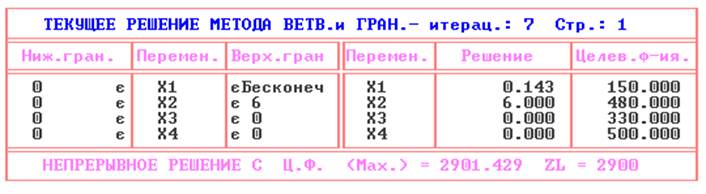
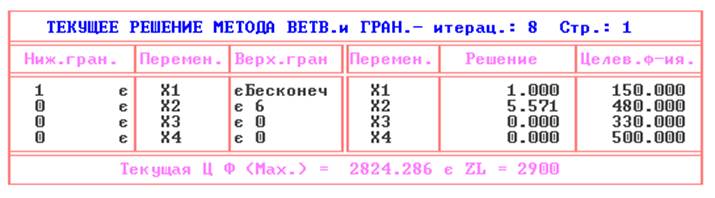
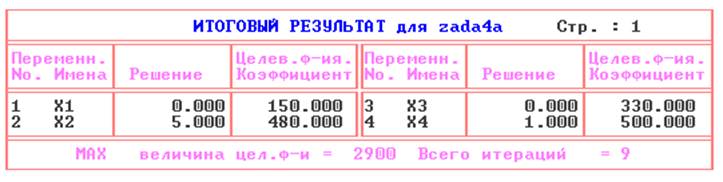
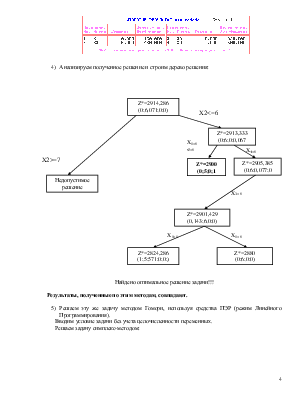
4)  Анализируем полученное решение и строим дерево решения:

 

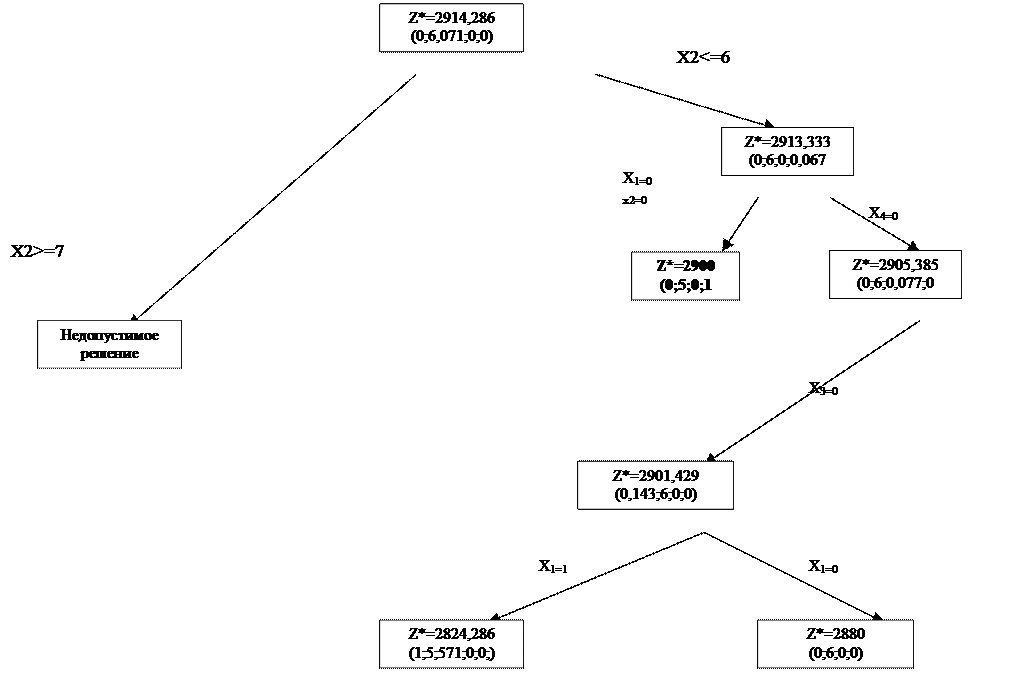
Найдено оптимальное решение задачи!!!

Результаты, полученные по этим методам, совпадают.

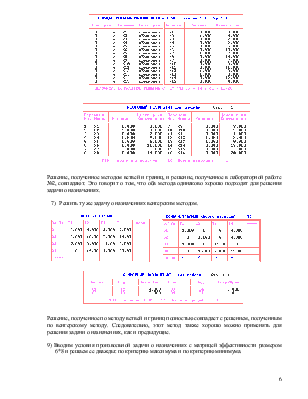
5)  Решаем эту же задачу методом Гомори, используя средства ПЭР (режим Линейного Программирования).

Вводим условие задачи без учета целочисленности переменных.

Решаем задачу симплекс-методом:

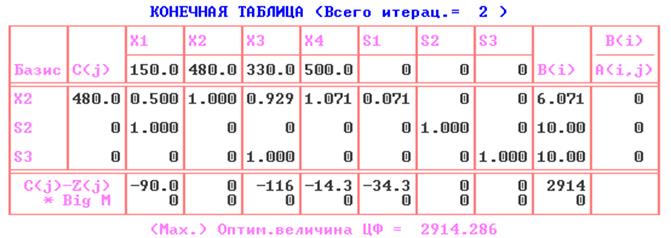
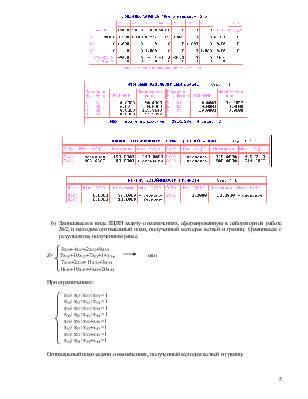
6)  Записываем в виде ЗЦЛП задачу о назначениях, сформированную в лабораторной работе №2, и находим оптимальный план, полученный методом ветвей и границ. Сравниваем с результатом, полученным ранее.

          3x₁₁+4x₁₂+2x₁₃+9x₁₄

Z=     5x₂₁+10x₂₂+7x₂₃+14x₂₄,                       min

          7x₃₁+2x₃₂+11x₃₃+3x₃₄

              0x₄₁+19x₄₂+4x₄₃+20x₄₄

 

При ограничениях:

х₁₁+х₁₂+х₁₃+х₁₄ =1

х₂₁+х₂₂+х₂₃+х₂₄ =1

х₃₁+х₃₂+х₃₃+х₃₄ =1

х₄₁+х₄₂+х₄₃+х₄₄ =1

х₁₁+х₂₁+х₃₁+x₄₁ =1

х₁₂+х₂₂+х₃₂+x₄₂ =1

х₁₃+х₂₃+х₃₃+x₄₃ =1

х₁₄+х₂₄+х₃₄+x₄₄ =1

Оптимальный план задачи о назначениях, полученный методом ветвей и границ:

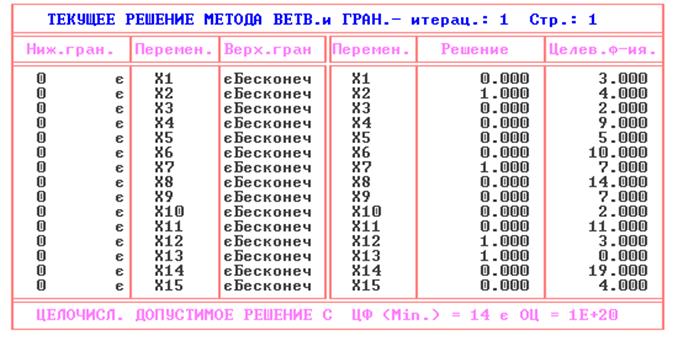
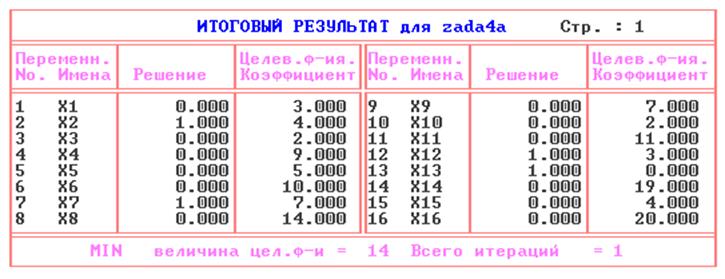
Решение, полученное методом ветвей и границ, и решение, полученное в лабораторной работе №2, совпадают. Это говорит о том, что оба метода одинаково хорошо подходят для решения задачи о назначениях.

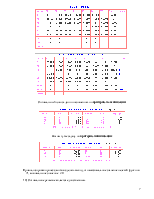
7)  Решить ту же задачу о назначениях венгерским методом.

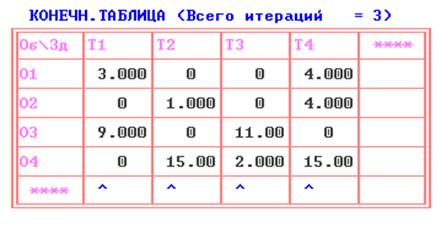
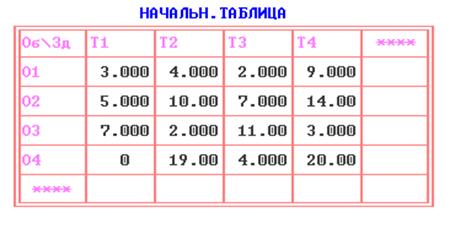
Решение, полученное по методу ветвей и границ полностью совпадает с решением, полученным по венгерскому методу. Следовательно, этот метод также хорошо можно применять для решения задачи о назначениях, как и предыдущие.

9) Вводим условия произвольной задачи о назначениях с матрицей эффективности размером 6*8 и решаем ее дважды: по критерию максимума и по критерию минимума.

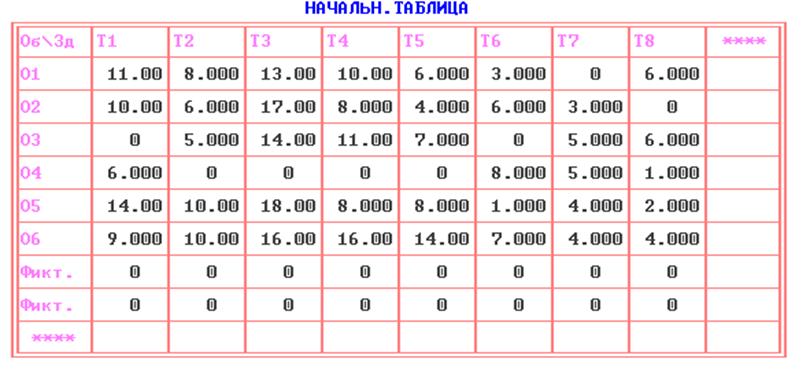
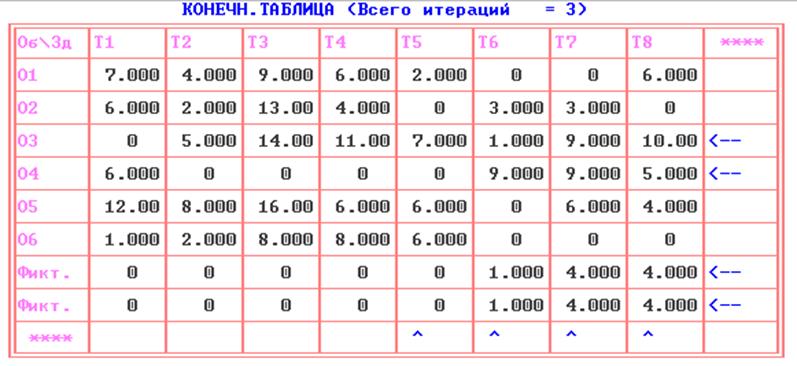
Оптимальный план задачи о назначениях по критерию максимизации:

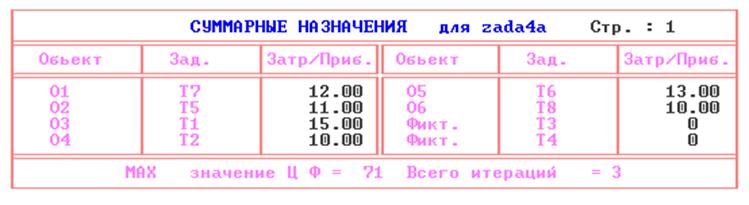
Решим ту же задачу по критерию минимизации:

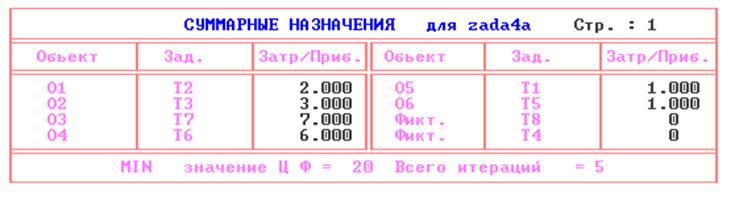
Проанализировав процесс, можно сделать вывод, что максимальное значение целевой функции = 71, минимальное значение =20.

10) Оптимальное решение является единственным.

Вывод: Мы приобрели практические навыки и опыт решения задач целочисленного линейного программирования на ЭВМ (для этого ознакомились с правилами работы в различных режимах), научились различать общие и частные модели ЗЦЛП, выбирать методы решения, анализировать результаты. Также были рассмотрены разные методы решения задачи о назначениях, которая была вновь решена методом ветвей и границ, а также венгерским методом.