b=0.26м - толщина ребра балки.
Действительная форма плиты переменной толщины и вутов заменяется в
расчетном
сечении прямоугольной формой с толщиной 
=0,17м
и шириной bf'=2,30м.
Центр тяжести, арматуры ориентировочно назначается на расстоянии as=0,12 м от нижней грани пояса балки.
Расчет на прочность по изгибающему моменту производим, начиная с наиболее
нагруженного сечения. Определяем в первом приближении высоту сжатой зоны бетона
х1 при действии расчетного момента Mi, где i — номер рассматриваемого сечения
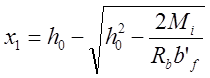
в 1-ом сечении х1=0,14м
в 2-ом сечении х1=0,18м
Т.к.
, то сечение работает как
прямоугольное и необходимая площадь рабочей
арматуры
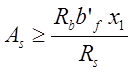
в 1-ом сечении As=0,02м2
в 2-ом сечении As=0,03м2
Задаваясь диаметром арматуры, определяем количество стержней:
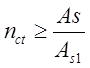
где nст — целое число стержней;
в 1-ом сечении nст =25
в 2-ом сечении nст =37
Asl =8,04см2 - площадь сечения одного стержня при диаметре арматуры 32 мм.
Рабочую арматуру в поясе балки можно располагать одиночными стержнями,
пучками по два-три стержня, а также в несколько рядов по высоте. При расположении арматуры в каркасах более чем в три ряда по высоте необходимо через три стержня
предусматривать просвет в один диаметр.
После уточнения площади As с учетом принятого диаметра и количества стержней
арматуры находим значение х2:
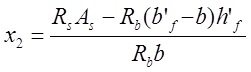
в 1-ом сечении х2 =0,087м
в 2-ом сечении х2 =0,512м
Окончательное значение z вычисляем по .формуле
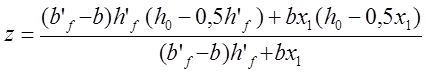
с подстановкой х2 вместо х1
в 1-ом сечении z =1.43м
в 2-ом сечении z =1.30м
Условие прочности сечения по изгибающему моменту записывается в виде
|
i=1 |
i=2 |
|
|
Мпр, кНм |
7187.96 |
9671.08 |
|
Мi, кНм |
6629.77 |
8400.87 |
х2< hf', необходимо сечение рассчитывать как прямоугольное, для чего в формулах принимаем b = bf'.
Расчет на трещиностойкость по касательным напряжениям. Расчет по касательным напряжениям выполняют в предположении упругой работы конструкции, но без учета бетона растянутой зоны. В расчете ограничивается величина касательных напряжений, действующих по нейтральной оси сечения. Касательные напряжения могут быть определены (приближенно) по формуле
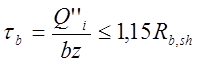
где Qi" — поперечная сила в рассматриваемом сечении от нормативных
b — толщина ребра балки;
z - плечо пары внутренних сил из расчета на прочность по изгибающему моменту.
в
0-ом сечении
=1758.40кПа
в
2-ом сечении
=756.99кПа
При переменной толщине ребра балки максимальная поперечная сила, воспринимаемая при
меньшей толщине ребра b2=0.26м
кН,
Расстояние от места изменения толщины до середины пролета будет равно
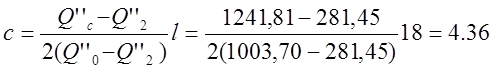м
Расчет на прочность по поперечной силе. При расчете изгибаемых железобетонных элементов на прочность по поперечной силе предполагается, что в предельном состоянии образуется наклонная трещина в бетоне, разделяющая элемент на две части. Поперечная сила в наклонном сечении воспринимается отогнутой арматурой, хомутами и бетоном сжатой зоны.
Места отгибов стержней рабочей арматуры согласуем с эпюрой действующих в балке изгибающих моментов. Для этого точки отгибов сносим на эпюру М, следя, чтобы предельный момент для оставшихся стержней рабочей арматуры не был меньше расчетного момента в сечении. При необходимости можно отгибать стержни группами по два-три в одном сечении. Эпюра предельных моментов (эпюра материалов) должна быть во всех сечениях объемлющей по отношению к эпюре расчетных моментов. Для построения эпюры материалов используем приближенную зависимость, считая, что предельный момент,
воспринимаемый сечением с одним стержнем рабочей арматуры
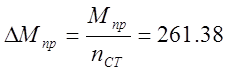кНм
где nст=37 - количество стержней рабочей арматуры в среднем сечении.
Графически
получаем делением максимальной ординаты
горизонтальными линиями на равные отрезки, число которых соответствует
количеству стержней рабочей арматуры. Точки пересечения горизонтальных линий с
эпюрой расчетных моментов определяют места возможного отгиба стержней. Наклонные
стержни должны равномерно армировать ребро главной балки. На всем участке
расположения отогнутой арматуры любое произвольно выбранное вертикальное
сечение должен пересекать хотя бы один наклонный стержень. Угол наклона
стержней к оси балки а обычно принимают равным
45°, но не более 60° и не менее 30°.
Не менее 1/3 стержней рабочей арматуры должны доводиться без отгибов до опоры.
Проверка прочности наклонного сечения на действие поперечной силы производится из условия
где Q=2061кН — максимальное значение поперечной силы от внешних нагрузок, расположенной по одну сторону от наклонного сечения;
=200МПа= 0,8Rs—расчетное
сопротивление арматуры отогнутых стержней или хомутов;
Аsi=8,04см2 и Аsw —площади поперечного сечения соответственно одного отогнутого стержня и всех ветвей одного хомута, пересекающих наклонное сечение;
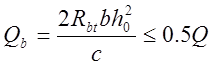- поперечное усилие,
передаваемое на бетон сжатой зоны сечения;
в
сечении 0 
=2579,72кН
в
сечении 2 =408,98кН
с — длина горизонтальной проекции сечения.
Наклонное сечение должно располагаться в пределах постоянной толщины ребра. На приопорных участках длиною 2hо=2*0,223=0,446м наклонное сечение составляет с продольной осью балки угол 45°, длина его горизонтальной проекции равна
с=h0-x=0,223-0=0,223м. На других участках наклонные сечения проверяются при длине проекции 0,223м=h0<c<2h0=2*0,223=0,446м Для сечения в середине пролета можно
принять с=2h0=0,446м.
Располагая схемой размещения отогнутых стержней, определяем количество стержней,
пересекающих
наклонное сечение и, соответственно, суммарную площадь 
=
Площадь всех ветвей одного хомута определяется
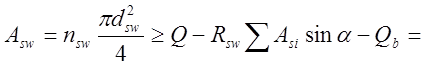
где dsw=12мм — диаметр хомутов
nsw — число ветвей одного хомута.
Шаг хомутов asw принимается не более: на концевых участках с длиною равной высоте балки— 10 см; на приопорных участках до четверти длины пролета — 15 см; на среднем участке — 20 см.
При
отсутствии отогнутых стержней на среднем участке балки (
)
прочность
наклонного сечения должна быть обеспечена за счет выбора соответствующего диаметра и
шага хомутов.
Стенки главных балок армируются продольной распределительной арматурой
d=12 мм с шагом не более 12 d в пределах трети высоты, считая от растянутой
грани, и с шагом не более 20d на остальной части высоты.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.