Министерство образования Российской Федерации
Новосибирский Государственный Технический Университет
Расчетно-графическая работа
Факультет бизнеса
Группа: ФБИ-
Выполнил студент:
Проверил преподаватель: Иванов Л.Н.
2007
Синтез комбинационных схем
Исходные данные:
|
Номер варианта |
Логическая функция |
|
3 |
0,9,10,14 |
Ход выполнения работы:
Задана логическая функция y = V(0,9,10,14)
Зная веса двоичных разрядов, представим функцию в эквивалентной записи, заменив десятичные числа соответствующими двоичными тетрадами
0 = 0000
9 = 1001
10 = 1010
14 = 1110
y = V(0000, 1001, 1010, 1110)
Теперь можно перейти к алгебраической форме, учитывая символ дизъюнкции в функции y и найти выражение представленное в СДНФ:
_ _ _ _ _ _ _ _ _
y = x1x2x3x4 + x1x2x3x4 + x1x2x3x4 + x1x2x3x4 , где x1 – старший разряд
Далее нужно минимизировать полученное выражение графическим методом, заполнив карту Карно (рис. 1): единицы записываются в те клетки карты, которые соответствуют кодовым комбинациям, обращающую функцию y в «1» (конституенты единиц)
|
_ x1 |
x1 |
||||
|
_ x2 |
1 |
1 |
_ x4 |
||
|
1 |
x4 |
||||
|
x2 |
|||||
|
1 |
_ x4 |
||||
|
_ x3 |
x3 |
_ x3 |
|||
Рис. 1 Карта Карно
В незаполненных клетках карты Карно – нули.
Теперь нужно выполнить операцию склеивания соседних единиц и записать минимизированную логическую функцию как дизъюнкцию полученных контуров склеивания (импликант):
_ _ _ _ _ _ _
ymin = x1x2x3x4 + x1x3x4 + x1x2x3x4
используя условные графические обозначения нужно показать эквивалентную микросхему, реализующую функцию ymin (рис. 2)
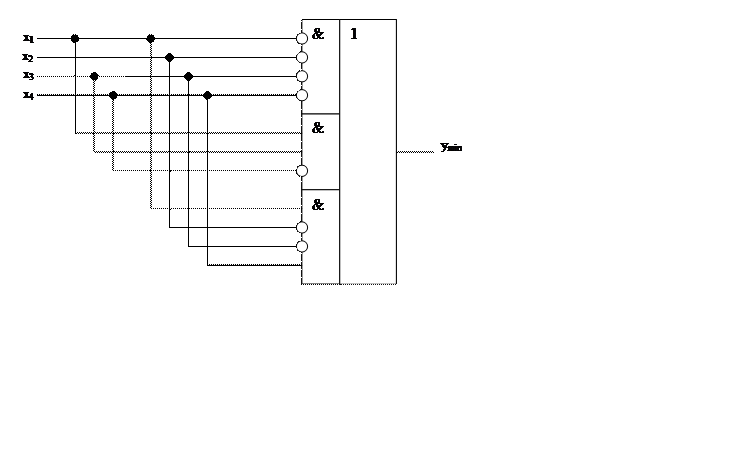
Рис. 2 Эквивалентная микросхема, реализующая функцию ymin
Интегральные схемы серии К155 реализованы в базисе И-НЕ. Поэтому выражение ymin необходимо привести к этому базису, применяя теорему
——————
——————
двойной инверсии (A + B = A + B) и теорему инверсии (правило де Моргана:
————— —— ——
(A + B = A + B)). Тогда получается:
—————————————————————————— ——————————————————————————
—————————————————————————— ———————— —————— ————————
––– ––– ––– ––– ––– ––– ––– ––– ––– ––– ––– ––– ––– –––
ymin = x1x2x3x4 + x1x3x4 + x1x2x3x4 = x1x2x3x4 · x1x3x4 · x1x2x3x4
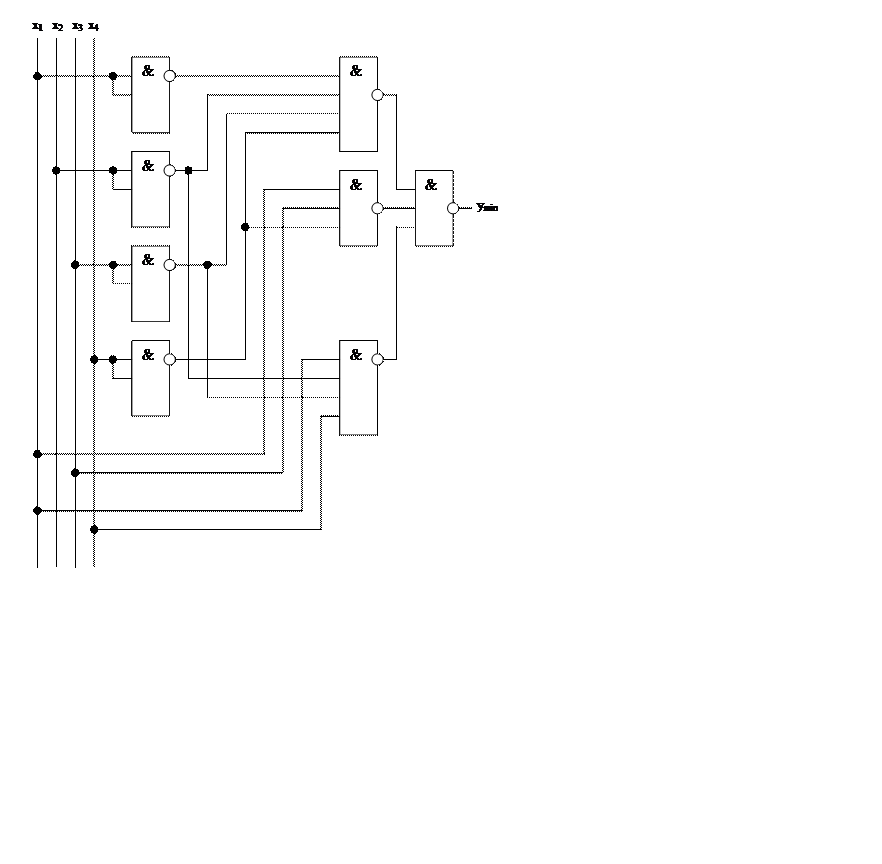
Теперь нужно построить и оформить принципиальную схему на элементах И-НЕ, реализующее преобразованное логическое выражение (рис. 3), также нужно составить спецификацию.
Далее определим время задержки переключения схемы Тз как время прохождения сигналов от входа к выходу по самой длинной последовательности цепи. Эта цепь в данном случае состоит из трех элементов. Следовательно, Тз = 3tз = 3 · 22 = 66 нс (tз = 22 нс – максимальное время переключения логического элемента И-НЕ).
Для второго варианта схемы с использованием элемента И-ИЛИ-НЕ время переключения Тз = 2tз’+ tз’’ = 2 · 22 + 30 = 74 нс, где tз’’ – время переключения логического элемента И-ИЛИ-НЕ (30 нс).
|
Позиционное обозначение |
Наименование микросхем |
Количество |
Примечание |
|
D1 |
К155ЛА3 |
1 |
- |
|
D2 |
К155ЛА1 |
1 |
- |
|
D3 |
К155ЛА4 |
1 |
Элемент D3.3 свободный |
Рис. 3 Принципиальная схема на элементах И-НЕ, реализующее преобразованное логическое выражение
Второй вариант схемы может быть реализован с использованием элемента И-ИЛИ-НЕ, если выражение ymin представить в виде:
—————————————————————————— ——————————————————————————
—————————————————————————— ———————— ————————————————
––– ––– ––– ––– ––– ––– ––– ––– ––– ––– ––– ––– ––– –––
ymin = x1x2x3x4 + (x1x3x4 + x1x2x3x4) = x1x2x3x4 · x1x3x4 + x1x2x3x4
Ему соответствует рис. 4
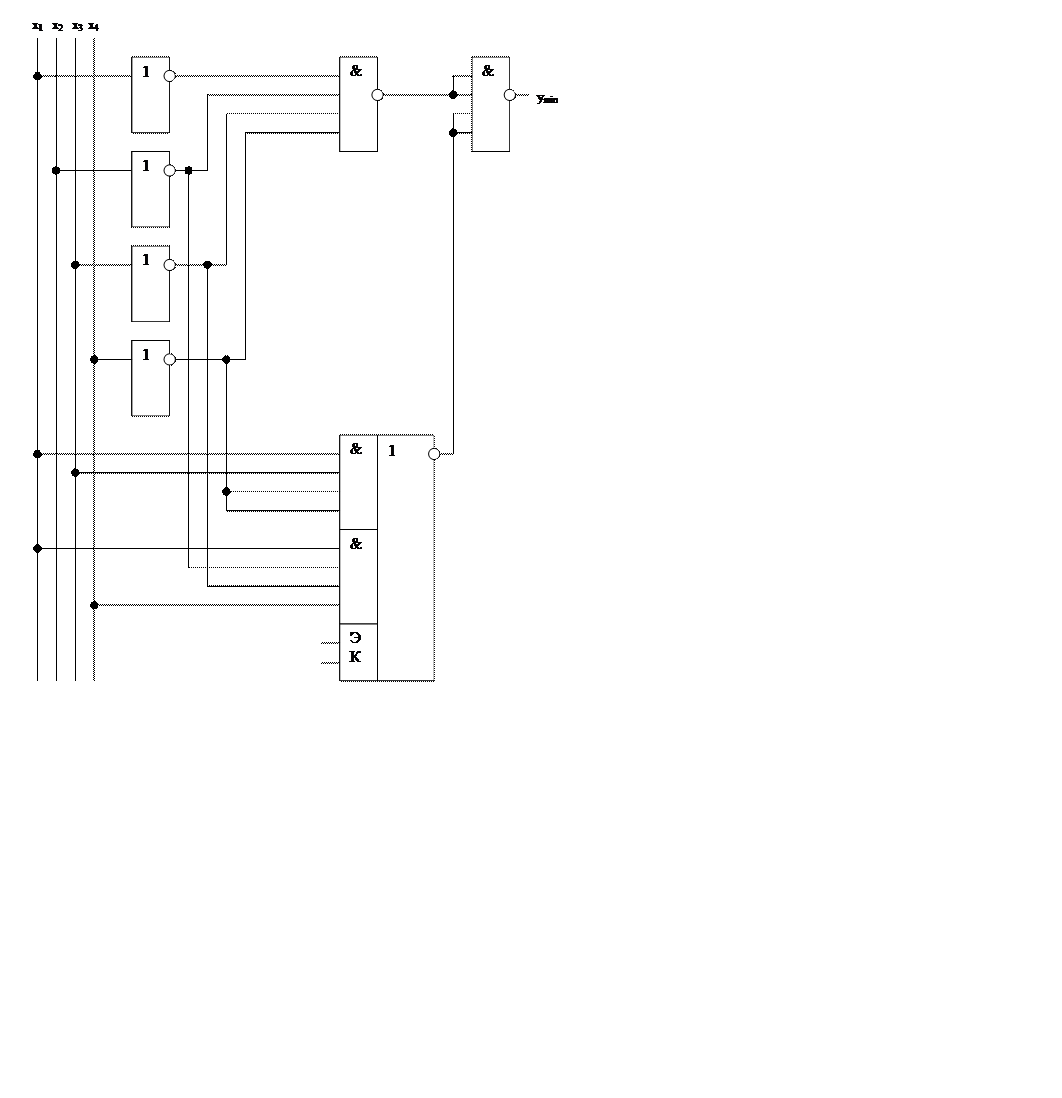
|
Позиционное обозначение |
Наименование микросхем |
Количество |
Примечание |
|
D1 |
К155ЛН1 |
1 |
Элементы D1.5, D1.6 свободны |
|
D2 |
К155ЛА1 |
1 |
- |
|
D3 |
К155ЛР4 |
1 |
- |
Рис. 4 Принципиальная схема на элементах И-ИЛИ-НЕ, реализующее преобразованное логическое выражение
Вывод:
В ходе выполнения работы были получены навыки построения эквивалентной микросхемы, реализующую функцию ymin, при помощи карты Карно. С помощью теоремы инверсии и правила де Моргана научился строить схемы в базисах И-НЕ и И-ИЛИ-НЕ, научился определять какие именно микросхемы входят в общую схему и какие элементы микросхем свободны. Также научился определять время задержки переключения схем.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.