Министерство Образования и науки Российской Федерации
НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
Факультет Бизнеса
Кафедра Экономической информатики
Расчетно-графическая работа
По теме: "ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ. ТЕОРИЯ ДВОЙСТВЕННОСТИ"
ВАРИАНТ - 14
Группа: ФБИ-51
Студент:
Преподаватель: Кириллов Ю. В.
Новосибирск
2007
Цель работы:
1. Понимать смысл, различать, осознанно использовать следующие понятия: математическая модель задачи линейного программирования (ЗЛП); формы записи ЗЛП; геометрическая интерпретация ЗЛП; линии уровня функции; градиент функции; двойственные задачи; двойственные оценки; устойчивость решения ЗЛП; устойчивость оценок.
2. Получить навыки, уметь: строить математические модели ЗЛП; переходить от одной формы записи ЗЛП к другой; решать графически ЗЛП с двумя переменными; строить модель задачи, двойственной к исходной; находить решение ЗЛП на основе решения задачи, двойственной к ней; интерпретировать полученные результаты в терминах решаемой задачи; проводить анализ устойчивости решения ЗЛП на основе геометрической интерпретации.
Условие задачи:
Коммерческая фирма предполагает осуществить оптовую закупку продовольствия, располагая для этого суммой Sрублей. Номенклатура продовольствия включает пять наименований. Покупная цена каждого вида продукта равна соответственно s1, s2, s3, s4 и s5 рублей за килограмм. В распоряжении фирмы имеются холодильные камеры общей площадью V кв. метров. Площадь, необходимая для хранения одного килограмма продукта каждого вида, равна соответственно v1, v2, v3, v4 кв. м; при этом продукт пятого вида хранению не подлежит и должен быть реализован немедленно. При своевременной реализации продукта каждого вида прибыль фирмы составит соответственно p1, p2, p3, p4 и p5рублей за килограмм.
Определить объемы закупки продовольствия каждого вида, при которых фирма может рассчитывать на максимальную прибыль.
Задание:
1. Записать математическую модель задачи.
2. Построить модель задачи, двойственной к заданной, и дать ее геометрическую интерпретацию.
3. Решить двойственную задачу графически. Используя полученный результат, найти решение исходной задачи.
4. Дать экономическую интерпретацию двойственным оценкам.
5. Произвести анализ устойчивости полученного решения и двойственных оценок на основе геометрической интерпретации двойственной задачи.
6. Решить задачу с помощью Пакета экономических расчетов (ПЭР) и сравнить результаты решения с результатами, полученными вручную.
Исходные данные:
|
№ вар |
S |
V |
s1 |
s2 |
s3 |
s4 |
s5 |
v1 |
v2 |
v3 |
v4 |
p1 |
p2 |
p3 |
p4 |
p5 |
|
14 |
25 000 |
40 |
60 |
110 |
65 |
25 |
40 |
0.1 |
0.5 |
1.0 |
1.0 |
18 |
55 |
65 |
50 |
8 |
Ход работы:
1. Составляем математическую модель:
Пусть: X1 - 1 кг 1-го вида продукции, X2 - 1 кг 2-го вида продукции, X3 - 1 кг 3-го вида продукции, X4 - 1 кг 4-го вида продукции, X5 - 1 кг 5-го вида продукции.
Тогда целевая функция принимает следующий вид:
Z=P1X1+ P2X2+ P3X3+ P4X4+ P5X5 à max
Z=18*X1+ 55*X2+ 65*X3+ 50*X4+ 8*X5 à max
Ограничения:
![]()
![]()
|
S1X1+ S2X2+ S3X3+ S4X4+ S5X5 <=S; V1X1+V2X2+V3X3+V4X4+V5X5 <=V, Xj >=0, j = 1…5 Xj – целые |
60*X1+110*X2+65*X3+25*X4+40*X5<=25000; 0,1*X1+0,5*X2+1*X3+1*X4+0*X5<=40, Xj >=0, j = 1…5 Xj – целые |
2. Рассматривается ЗЛП в симметричной форме:
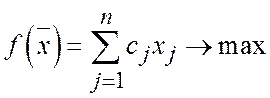 (1.1)
(1.1)
при ограничениях
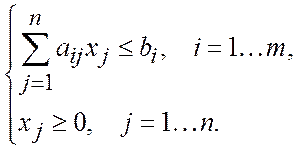 (1.2)
(1.2)
Двойственная задача будет иметь вид:
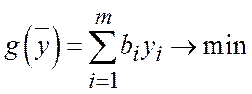 (1.3)
(1.3)
при ограничениях
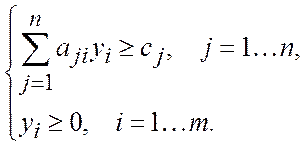 (1.4)
(1.4)
В соответствии с формулами 1.3 и 1.4 составим модель двойственной задачи:
Целевая функция: Z=Y1S+Y2Và min
Z=Y1*25000+Y2*40à min
Ограничения:
|
y1s2+y2v2>=p2, y1s3+y2v3>=p3, y1s4+y2v4>=p4, y1s5+y2v5>=p5, y1,y2>=0; |
y1*110+y2*0,5>=55, y1*65+y2*1,0>=65, y1*25+y2*1,0>=50, y1*40+y2*0>=8, y1,y2>=0; |
Решаем двойственную задачу графическим методом:
Построим линии:
![]() y1*10/3+y2/180=1,
y1*10/3+y2/180=1,
y1*2+y2/110=1,
y1*1+y2/65=1,
y1/2+y2/50=50,
y1*5+y2*0=1,
Строим линию уровня:
Тогда точка В точка оптимума (0,2; 66);
Подставляем эту точку в целевую функцию двойственной задачи:
Z=25000*0,2+40*66=7640
Из второй теоремы двойственности найдем решение прямой задачи:
![]()
![]() (60*0,2 + 0,1*66 – 18)*X1* = 0
0,6*X1* = 0 X1* = 0
(60*0,2 + 0,1*66 – 18)*X1* = 0
0,6*X1* = 0 X1* = 0
(110*0,2 + 0,5*66 – 55)*X2* = 0 0*X2* = 0 X2* ≠ 0
(65*0,2 + 1,0*66 – 65)*X3* = 0 14*X3* = 0 X3* = 0
(25*0,2 + 1,0*66 – 50)*X4* = 0 21*X4* = 0 X4* = 0
(40*0,2 – 8)*X5* = 0 0*X5* = 0 X5* ≠ 0
Таким образом, в плане X* прямой задачи только координаты x1 и x3 отличны от нуля. Согласно той же теореме о двойственности, x2* и x5* должны удовлетворять следующим соотношениям:
![]()
(110*X2*+40*X5*-25000)*y1=0,
(0.5*X2*+0*X5*-40)*y2=0,
Т.к. y1*>0 и y2*>0, то:
X2* = 80; X5* = 405;
Итак, решение исходной задачи: X* = (0;40;0;0;405)
Zпр* = Zдв* = 7640
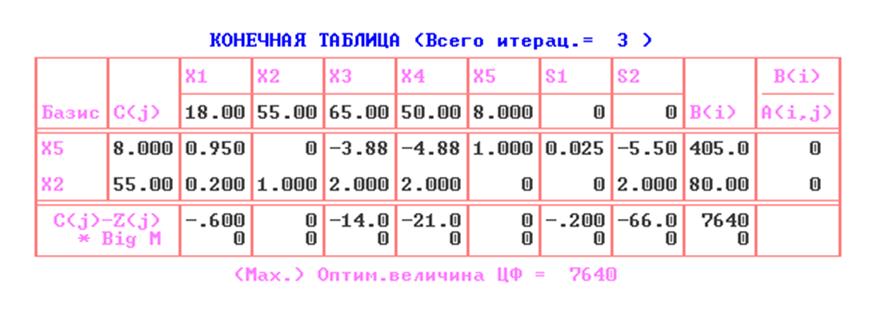

Теперь проведем экономический анализ полученного решения.
X* = (x1* = 0; x2* = 80; x3* = 0; x4* = 0; x5* = 405; x6* = 0; x7* = 0).
Пользуясь таблицей соответствия и конечной симплекс – таблицей решенной задачи, выпишем все переменные двойственной задачи:
Y* = (y1* = 0,2; y2* = 66; y3* = 0,6; y4* = 0; y5* = 14; y6* = 21; y7* = 0).
Величины x2* и x5* показывают, что товары первого типа необходимо закупить в количестве 80 штук, третьего типа – в количестве 405 штук. Товары 1, 3, 4 типов закупать нецелесообразно. Двойственные оценки y3*, y5*, y6* это подтверждают.
Из второй теоремы двойственности следует:
(1) y3* = a11* y1* + a21* y2* = 60*0,2 + 0,1*66 – 18 = 0,6 (степень нерентабельности товара первого типа)
Аналогично:
(2) y5* = a13* y1* + a23* y2* = 65*0,2 + 1,0*66 – 65 = 14 (степень нерентабельности товара третьего типа)
(3) y6* = a14* y1* + a24* y2* = 25*0,2 + 1,0*66 – 2 = 21 (степень нерентабельности товара четвертого типа)
Из (1), (2), (3) следует, что товар 4-го типа является самым «невыгодным», т.е. его закупка обходиться дороже всего.
Обратимся к дополнительным переменным прямой задачи: их значения показывают остатки соответствующего вида ресурса после выполнения оптимального плана.
Из ограничения прямой задачи по деньгам следует:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.