ИЗУЧЕНИЕ ВЫНУЖДЕННЫХ ЭЛЕКТРОМАГНИТНЫХ КОЛЕБАНИЙ В ПОСЛЕДОВАТЕЛЬНОМ КОЛЕБАТЕЛЬНОМ КОНТУРЕ
Цель работы. Изучение с помощью электронного осциллографа вынужденных электромагнитных колебаний в последовательном контуре; наблюдение резонанса напряжений и снятие резонансных кривых; определение двумя способами добротности контура; расчёт внутреннего активного электросопротивления генератора.
Вынужденными называются колебания, возникающие в какой-либо системе под действием периодической внешней (вынуждающей) силы. Характер вынужденных колебаний определяется свойствами колебательной системы и свойствами источника вынуждающей силы.
В работе научаются линейные вынужденные колебания в последовательном электромагнитном контуре с сосредоточенными параметрами R, L, С (рис. 1). Источником вынуждающей силы является генератор, с бесконечно малым внутренним электросопротивлением, ЭДС генератора изменяется по гармоническому закону ε = ε0cosΩt.
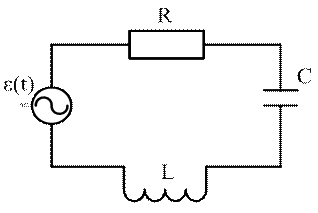
Рис. 1
Для мгновенных значений токов и напряжений в исследуемом контуре можно записать закон Ома в обобщенной форме
|
|
(1) |
где U — разность потенциалов на обкладках конденсатора; R — полное активное электросопротивление цепи контура; I — квазистационарный электрический ток в цепи контура.
Так как на экране осциллографа наблюдается временнáя зависимость U(t), решим уравнение(1) относительно U. Выполнив замены
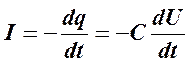 ,
, 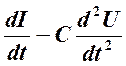
и введя обозначения 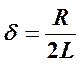 и
и
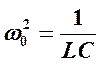 , получим линейное дифференциальное
уравнение второго порядка с правой частью, описывающее вынужденные колебания
разности потенциалов на обкладках конденсатора:
, получим линейное дифференциальное
уравнение второго порядка с правой частью, описывающее вынужденные колебания
разности потенциалов на обкладках конденсатора:
|
|
(2) |
Здесь ω0 — круговая (циклическая)частота собственных незатухающих колебаний; δ— коэффициент затухания собственных колебаний; Ω и ε0 — круговая частота и амплитуда вынуждающей ЭДС.
Общее решение уравнения (2) для
случая ![]() имеет вид
имеет вид
|
|
(3) |
где ![]() — круговая
частота затухающих собственных колебаний; φ0
и α — начальные фазы запухающих и вынужденных колебаний разности потенциалов
на конденсаторе. Из уравнения (3) видно, что в начале действия внешней силы
характер колебаний изменяется во времени, но с затуханием собственных
колебаний в контуре устанавливаются гармонические колебания вида
— круговая
частота затухающих собственных колебаний; φ0
и α — начальные фазы запухающих и вынужденных колебаний разности потенциалов
на конденсаторе. Из уравнения (3) видно, что в начале действия внешней силы
характер колебаний изменяется во времени, но с затуханием собственных
колебаний в контуре устанавливаются гармонические колебания вида
|
|
(4) |
Амплитуда и начальная фаза установившихся колебаний:
|
|
(5) |
|
|
(6) |
определяются амплитудой вынуждающей ЭДС ε0 и частотой Ω, а также параметрами контура R, L, С.
По мере приближения частоты колебаний вынуждающей силы Ω к частоте собственных электромагнитных колебаний ω0 в последовательном контуре наступает так называемый резонанс напряжений, т. е. резкое возрастание амплитуд напряжений вынужденных колебаний на реактивных элементах контура L и С. При этом в колебательный контур от внешнего источника поступает наибольшая мощность.
Исследуя (5) на экстремум получим, что разность потенциалов на конденсаторе достигает максимального, т. е. резонансного значения:
|
|
(7) |
при частоте вынуждающей ЭДС
|
|
(8) |
называемой круговой резонансной частотой.
Графическая зависимость амплитуды U0 от частоты вынуждающей ЭДС называется резонансной кривой или резонансной характеристикой контура. На рис. 2 представлены резонансные кривые для различных значений коэффициента затухания δ. Очевидно, что резонансные значения амплитуды и частоты убывают с ростом δ (δ1 < δ2 < δ3, см. рис. 2). Следует отметить, что максимальная величина тока в последовательном контуре достигается при частоте Ω =ω0 для любых значений δ.
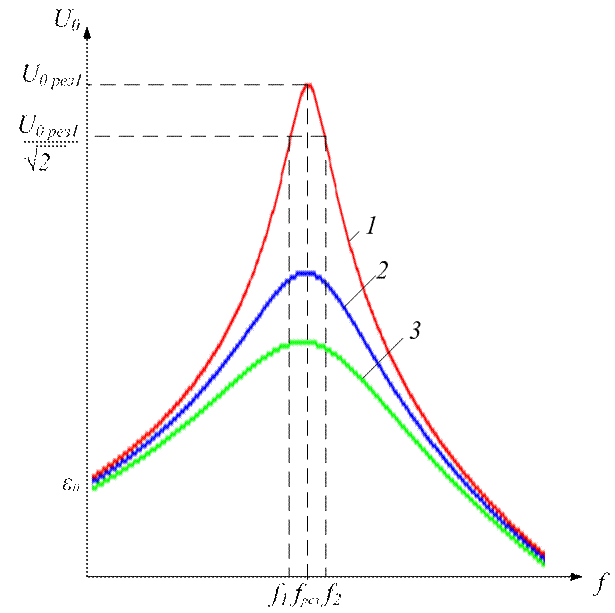 Рис. 2.
Рис. 2.
Резонансные свойства линейных колебательных систем, в частности электромагнитных контуров, характеризуется добротностью. Добротность Q это есть умноженное на 2π отношение имеющейся в контуре электромагнитной энергии к средней энергии потерь за один период колебаний.
Пренебрегая электромагнитным излучением контура и считая, что вся электромагнитная энергия сосредоточена в магнитном поле тока катушки и электрическом поле конденсатора, а потери связаны с протеканием тока по электросопротивлений R (диссипативные потери), можем величину добротности контура рассчитать по формуле:
|
Q |
(9) |
где R = r + RL + Rвнеш — полное активное электросопротивление цепи контура; r — внутреннее активное электросопротивление генератора (r << R); RL — активное сопротивление катушки и соединительных проводов; Rвнеш — активное внешнее электросопротивлений, включенное в контур.
Так как в момент резонанса амплитуда колебаний в Q раз превышает амплитуду внешней ЭДС, то при малых значениях δ соотношение (7) принимает вид
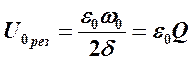 ,
,
и для добротности получим выражение
|
|
(10) |
Добротность контура можно также
рассчитать по ширине резонансной кривой. Ширина резонансной кривой (или полоса
пропускания контура) есть интервал частот Δf = f2 - f1
на границах которого энергия, запасенная в контуре при резонансе, убывает в два
раза, т. е. амплитуда колебаний U0 отличается от амплитуды
при резонансе в ![]() раз (см. рис.2).
раз (см. рис.2).
Для заданной величины δ добротность численно равна отношению резонансной частоты к ширине резонансной кривой:
|
|
(11) |
т. е. ширина резонансной кривой тем уже, чем больше добротность контура.
ОПИСАНИЕ УСТАНОВКИ
Схема лабораторной установки для исследования вынужденных электромагнитных колебаний изображена на рис. 3.
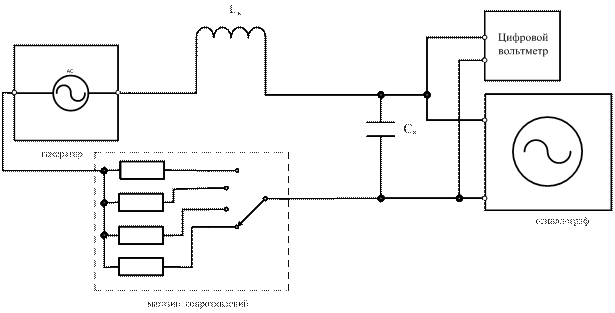
Рис.3. Схема лабораторной установки.
Колебательный контур состоит из последовательно соединенных конденсатора ёмкостью Ск, катушки индуктивности Lк и магазина сопротивлений R, который может поочередно включаться в контур. Значения ёмкости Ск, индуктивности Lк и электросопротивлений RL, указаны на панели установки.
Для возбуждения вынужденных колебаний используется генератор синусоидальных колебаний с несколькими диапазонами частот в пределах fг = 1 ÷ 20 кГц. Частота выходного сигнала генератора изменяется грубо путем переключения диапазонов частот и плавно в пределах выбранного диапазона ручкой плавной подстройки частоты. Отсчёт частоты производится по шкале частот выбранного диапазона. Резонансная частота соответствует наибольшей амплитуде электромагнитных колебаний при заданном значении R.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.