Определение приведённого момента инерции системы. Определение заданных критериев для трехфазного асинхронного электродвигателя с короткозамкнутым ротором

Задание по контрольной работе

Задача 1. Для трехфазного асинхронного электродвигателя с короткозамкнутым ротором, имеющего номинальную мощность , включенного под напряжение сети , определить:

– способ соединения статорных обмоток и вычертить схему подключения электродвигателя;

– номинальный вращающий момент ;

– максимальный (критический) момент ;

– пусковой момент ;

– линейные и фазные номинальные токи ;

– пусковые токи ;

– скольжение при номинальной нагрузке ;

– критическое скольжение ;

– мощность, потребляемая из сети  при номинальной нагрузке.

Построить механическую характеристику электродвигателя  по точкам, соответствующим скольжениям .

Определить для указанных точек скольжений моменты сопротивления механизма, приведённые к угловой скорости вращения вала электродвигателя.

Построить приведённую механическую характеристику механизма  в одних координатах с характеристикой двигателя.

Определить значения момента на валу электродвигателя при установившемся режиме работы.

В тех же координатах построить график избыточного момента .

Задача 2. Определить приведённый момент инерции системы . С учетом данных задачи 1 определить время разбега электропривода от неподвижного состояния до номинальной угловой скорости вращения. Построить график зависимости угловой скорости вращения от времени  при разгоне, совместив координату  с графиком задачи 1.

Задача 3. По 4…6 точкам рассчитать и построить кривые нагрева и охлаждения электродвигателя при номинальной длительной нагрузке. Аналитическим и графическим способами определить постоянные времени при нагреве  и охлаждения  и установившееся превышение температуры двигателя над температурой окружающей среды .

Определить допустимую мощность электродвигателя, если он будет работать в повторно-кратковременном режиме с заданной ПВ%.

Задача 4. по результатам задач 1…3 произвести проверку устойчивости пуска электродвигателя при снижении питающего напряжения на , и проверку устойчивости работы электродвигателя привода при номинальной нагрузке при снижении питающего напряжения на . Решение выполнить графически в относительных координатах .

Решение Задачи 1.

Номинальное напряжение двигателя , напряжение сети , следовательно, обмотки двигателя нужно соединить «треугольником».

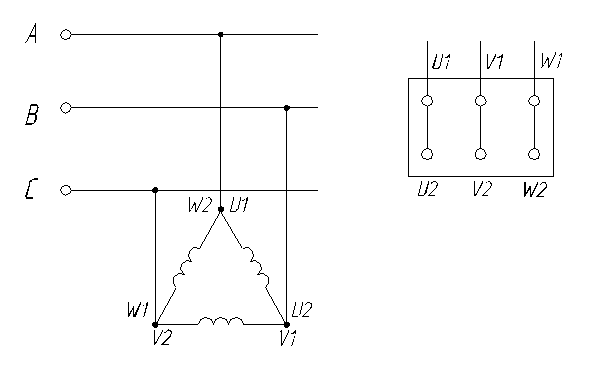
Рисунок 1 – Соединение обмоток двигателя «треугольником»

Определяем номинальный момент двигателя

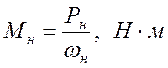,                                             (1)

где  – номинальная мощность на валу электродвигателя, =5500Вт;

        – номинальная угловая скорость вала, определяется по формуле

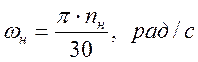,                                            (2)

Номинальную частоту  вращения, находим через номинальное скольжение

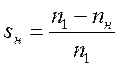 тогда ,

где – частота вращения магнитного поля, мин^-1.

Частоту вращения магнитного поля находим из выражения

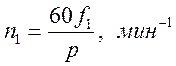                                            (3)

где  – частота питающей сети, ;

        – число пар полюсов обмотки статора, .

Подставляем исходные данные в формулы и получаем

,

,

,

.

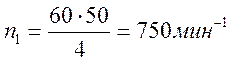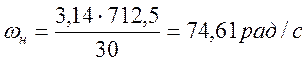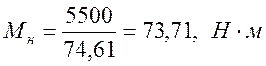Определяем критический момент по формуле

,                                            (4)

где – перегрузочная способность электродвигателя, .

Получаем

.

Определяем пусковой момент по формуле

,                                            (5)

где – кратность пускового момента, .

Получаем .

Определяем линейные и фазные номинальные токи . При соединении «треугольником» , а линейные и фазное напряжение .

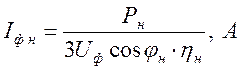,                                            (6)

где – фазное напряжение, ,

       – номинальный коэффициент мощности, ,

        – к.п.д. электродвигателя, .

Подставляем числа в формулы и получаем

,

.

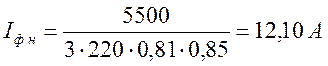Определяем пусковые токи , через кратность пускового тока 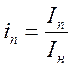, следовательно , при значении  получаем

,

.

Определяем критическое скольжение по формуле

.                                            (7)

Подставляем числа и получаем

.

Мощность, расходуемая электродвигателем из сети

.                                            (8)

Получаем .

Определение момента двигателя  для построения механической характеристики  производиться по различным формулам. При скольжении малых (от 0 до 0,3) для упрощения расчетов пользуемся формулой Клосса

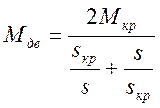.                                            (9)

При скольжениях больших (от 0,3 до 1) значение момента, полученные расчетом по формуле Клосса, не точны, чем больше скольжение, тем больше ошибка. Поэтому будем пользоваться формулами

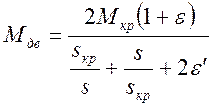,                                             (10)

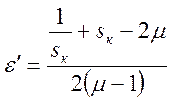,                                            (11)

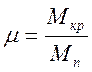 .                                            (12)

Для  получаем

.

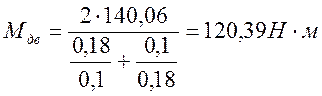Для  получаем

,

,

,

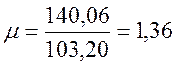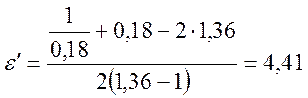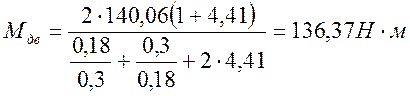Считаем для остальных значений скольжения и полученные данные заносим в таблицу 1. По данным таблицы 1 строим механическую характеристику электродвигателя  (рисунок 2); по горизонтали откладываем ; по вертикали откладываем .

Находим номинальную частоту вращения рабочей машины

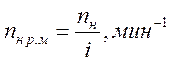,                                            (13)

где – передаточное число редуктора.

Получаем

.

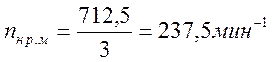Уравнение механической характеристики рабочей машины, приведенное к частоте вращения вала двигателя имеет вид

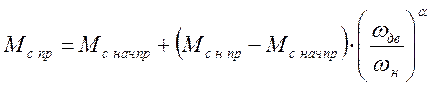,                                            (14)

где – номинальный приведенный момент сопротивления механизма, его принимаем равным номинальному моменту двигателя,  ;

      – начальный приведённый момент сопротивления механизма, можно принять равным , ;

        – текущее значение угловой скорости вращения электродвигателя, рад/с;

         – показатель степени уравнения (для вентилятора, насоса ).

Текущая угловая скорость вращения вала электродвигателя  может быть выражена через номинальную  приближенно так:

.

Тогда предыдущее уравнение приведённого момента механизма запишется:

.                                            (15)

При скольжении  получаем момент сопротивления

.

Аналогично считаем момент сопротивления  механизма для остальных значений скольжений, и полученные данные заносим в таблицу 1. Далее строим механическую характеристику рабочей машины на рисунке 2.

Таблица 1 – Зависимость момента двигателя и момента сопротивления механизма от угловой скорости.

Угловая скорость	78,54	74,61	70,69	64,73	62,83	54,98	39,27	0
Скольжение	0	0,05	0,10	0,18	0,20	0,30	0,50	1,00
Момент двигателя	0	73,71	120,39	140,06	138,90	136,37	126,12	103,20
Момент сопр. мех.	73,71	67,96	62,51	54,80	52,48	43,64	29,49	14,74
Избыточный момент	-73,71	5,75	57,88	85,25	86,41	92,73	96,63	88,46

Момент сопротивления на валу машины находим по формуле

.

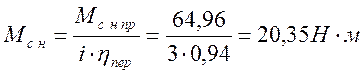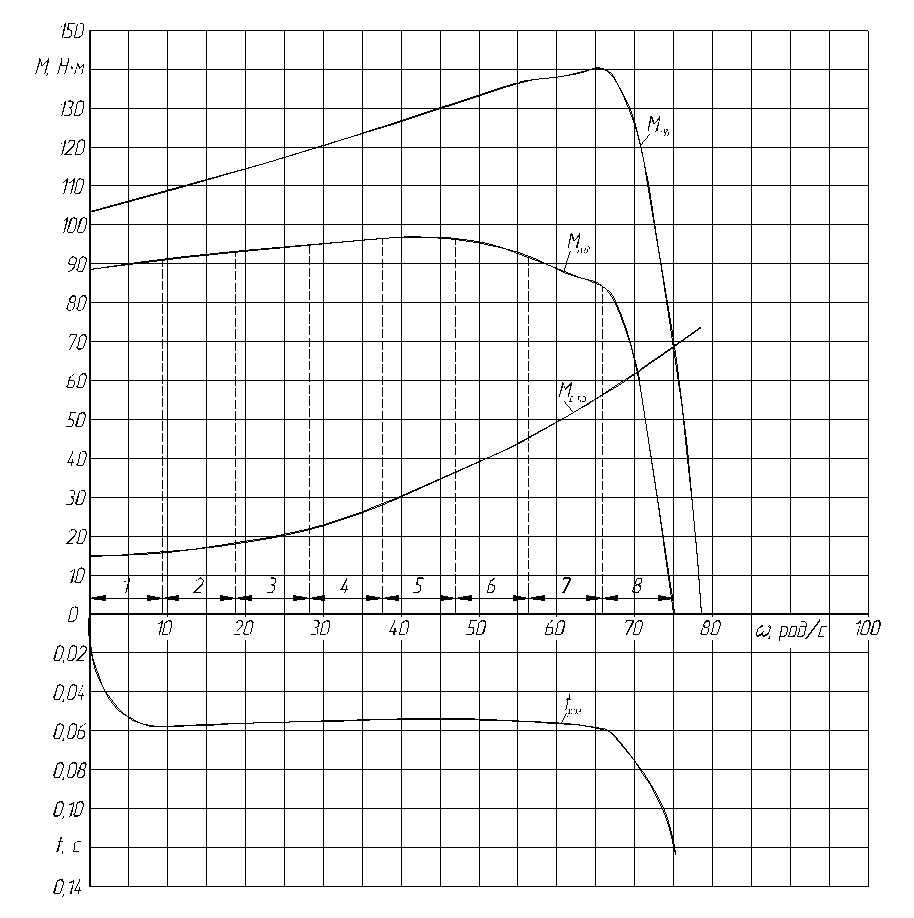
Рисунок 2 – механические характеристики электродвигателя и рабочей машины, избыточный момент и время разгона электропривода.

Решение Задачи 2.

Находим приведённый момент инерции электропривода  по формуле

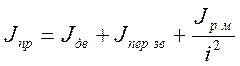,                                            (16)

где – момент инерции двигателя, ;

        – момент инерции передаточного звена (редуктора), определяется по соотношению ; коэффициент ,