Оптимизация грузопотоков (решение транспортной задачи в EXCEL)

Для решения транспортной задачи в EXCEL нам потребуется инструмент Поиск решения из меню Сервис. С помощью его можно искать решение систем уравнений, которые к тому же могут содержать ограничения.  Если этого инструмента в меню нет, то его надо установить. Для этого в CD-привод ставим установочный диск Microsoft Office, затем в меню Сервис нажимаем на инструмент Надстройки… , в поле Доступные надстройки ставим галочку напротив инструмента Поиск решения (рисунок 1), далее нажимаем ОК. Далее выскочит окно, нажимаем кнопку Да, и компьютер начнет устанавливать этот инструмент.

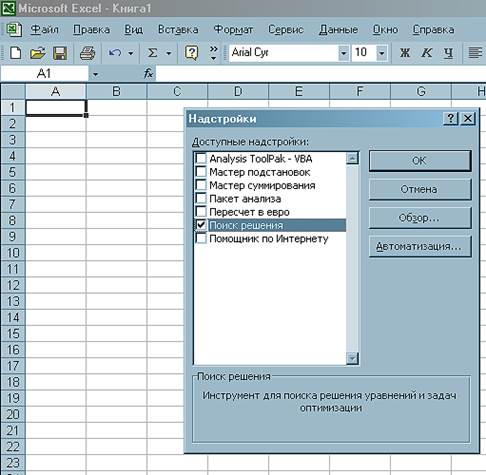
Рисунок 1 – Установка инструмента Поиск решения

Исходные данные для решения транспортной задачи целесообразно представить в виде двух таблиц (рисунок 2), в первой представлены значения расстояния от поставщика к получателю. Во второй таблице представлены значения наличия груза у каждого поставщика; значения потребности груза у каждого потребителя; поле изменяемых ячеек переменных С18:L27; вспомогательный столбец и вспомогательная строка Сумма.

Для подсчета суммы в ячейке B28 ставим знак «=», верхнем правом углу ищем значок f_x , нажимаем его, откроется окно Мастер функций, в поле Категория выбираем Математические, ищем из списка функцию СУММ, нажимаем ОК, откроется окно Аргументы функции, нажимаем на значок , мышкой выделяем ячейки B18:B27, нажимаем Enter, затем ОК, таким образом мы записываем формулу в ячейке B28

=СУММ(B18:B27)

Аналогично для подсчета суммы в ячейке М17, получаем запись

=СУММ(C17:L17)

Целевая ячейка D30 должна содержать формулу 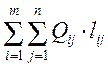, для программы  это будет функция =СУММПРОИЗВ(массив1;массив2;массив3;…)

Она выводит суммы произведений соответствующих элементов диапазонов или массивов. То есть в нашем случае выводит сумму произведений расстояний до поставщиков (диапазон ячеек С3:L12) и количество перевозимого груза (диапазон ячеек С18:L27).

Для этого в ячейке С18 ставим знак «=», верхнем правом углу ищем значок f_x , нажимаем его, откроется окно Мастер функций, в поле Категория выбираем Математические, ищем функцию СУММПРОИЗВ, нажимаем ОК, откроется окно Аргументы функции, в строке Массив1 нажимаем на значок , мышкой выделяем ячейки С3:L12, нажимаем Enter, в строке Массив2 нажимаем на значок , мышкой выделяем ячейки С18:L27, нажимаем Enter, затем ОК, таким образом мы записываем формулу в ячейке С18

=СУММПРОИЗВ(C3:L12;C18:L27).

Эта функция и есть общее уравнение для отыскания минимального среднего расстояния перевозки.

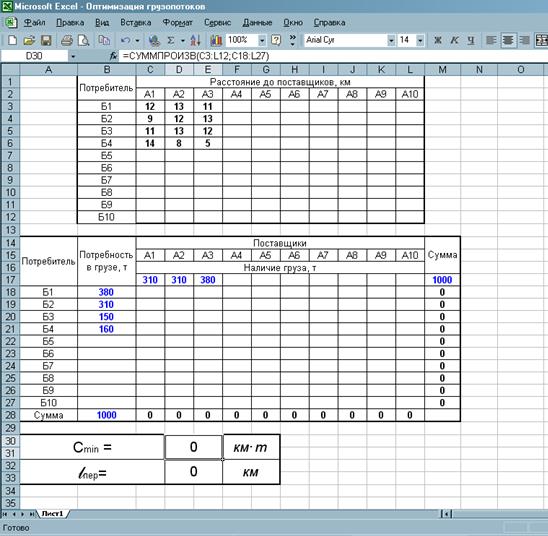
Рисунок 2 – Исходные данные

Используя меню Сервис→Поиск решения, открываем инструмент Поиск решения (рисунок 3), в котором в поле Установит целевую ячейку нажимаем значок  , мышкой нажимаем на ячейку D30, нажимаем Enter, ставим точку напротив слов минимальному значению, в поле Изменяя ячейки нажимаем значок  , мышкой выделяем ячейки C18:L27, нажимаем Enter,

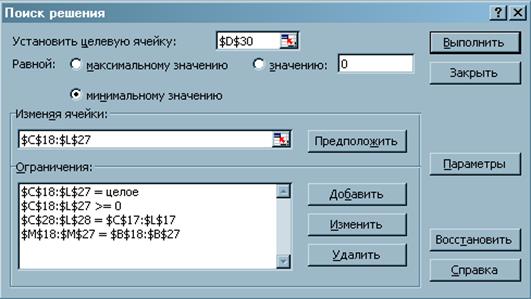
Рисунок 3 – Окно инструмента Поиск решения

Далее нужно добавить ограничения:

1) во все j-е пункты получения груза из i-го пункта отправления может быть вывезено только Q_j  единиц груза

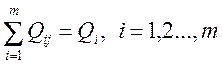
2) из всех i-х пунктов отправления j-му пункту получения должно быть доставлено только Q_i единиц груза

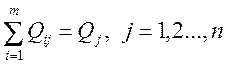
3) искомые переменные не могут быть отрицательными числами

Для программы эти ограничения будут выглядеть следующим образом:

1) Нажимая на кнопку    Добавить   переходим в окно Добавление ограничения. В поле Ссылка на ячейку: нажимаем на значок , мышкой выделяем поля С28:L28, нажимаем Enter, получаем запись &С&28:&L&28, в среднем поле из списка выбираем «=», в поле Ограничения:нажимаем на значок , мышкой выделяем поля С17:L17, нажимаем Enter, получаем запись &С&17:&L&17. Таким образом получаем ограничение

&С&28:&L&28 = &С&17:&L&17.

2) Нажимая на кнопку    Добавить   переходим в окно Добавление ограничения. В поле Ссылка на ячейку: нажимаем на значок , мышкой выделяем поля М18:М27, нажимаем Enter, получаем запись &М&18:&М&27, в среднем поле из списка выбираем «=», в поле Ограничения:нажимаем на значок , мышкой выделяем поля В18:В27, нажимаем Enter, получаем запись &В&18:&В&27. Таким образом получаем ограничение

&М&18:&М&27 = &В&18:&В&27.

3) Нажимая на кнопку    Добавить   переходим в окно Добавление ограничения. В поле Ссылка на ячейку: нажимаем на значок , мышкой выделяем поля C18:L27, нажимаем Enter, получаем запись &С&18:&L&27, в среднем поле из списка выбираем знак «>=», в поле Ограничения:ставим число 0. Таким образом получаем ограничение

&С&18:&L&27 >= 0

4) Нажимая на кнопку    Добавить   переходим в окно Добавление ограничения. В поле Ссылка на ячейку: нажимаем на значок , мышкой выделяем поля C18:L27, нажимаем Enter, получаем запись &С&18:&L&27, в среднем поле из списка выбираем слово цел, в поле Ограничения:получаем запись целое. Таким образом получаем ограничение

&С&18: &L&27 = целое

Нажимаем на кнопку Параметры , ставим галочку напротив слов Линейная модель и Неотрицательные значения.

Далее запускаем процедуру вычисления, щелкнув по кнопке Выполнить.

Найдя оптимальное решение, откроется диалоговое окно Результаты поиска решения, нажимаем на кнопку ОК (рисунок 4).

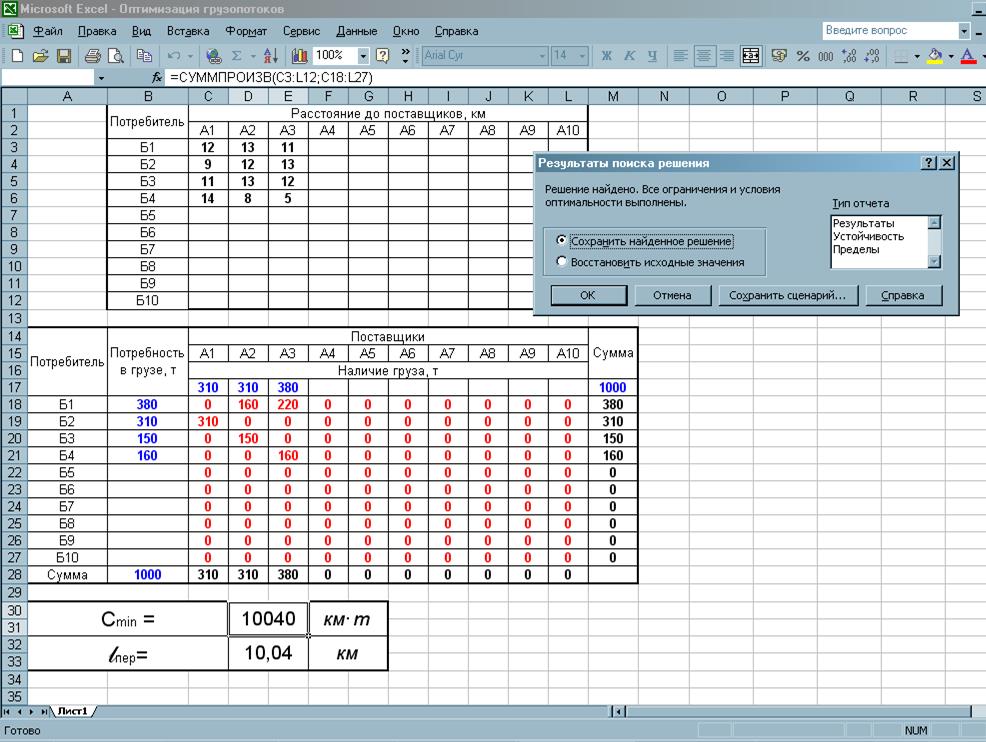
Рисунок 4 – Результаты поиска решения

Оптимальное решение данной задачи показывает:

1.  Поставщик А1 будет поставлять груз потребителю Б2 в количестве 310т на расстояние 9 км (клетка А1-Б2).

2.  Поставщик А2 будет поставлять груз потребителю Б1 – 160т на 13 км (клетка А2-Б1), а также потребителю Б3 – 150т на 13 км (клетка А2-Б3).

3.  Поставщик А3 будет поставлять груз потребителю Б1 – 220т на 11 км (клетка А3-Б1), а также потребителю Б4 – 160т на 5 км (клетка А3-Б4).

Среднее расстояние перевозки составит: l_пер= 10,04 км.