Для решения транспортной задачи в EXCEL нам потребуется инструмент Поиск решения из меню Сервис. С помощью его можно искать решение систем уравнений, которые к тому же могут содержать ограничения. Если этого инструмента в меню нет, то его надо установить. Для этого в CD-привод ставим установочный диск Microsoft Office, затем в меню Сервис нажимаем на инструмент Надстройки… , в поле Доступные надстройки ставим галочку напротив инструмента Поиск решения (рисунок 1), далее нажимаем ОК . Далее выскочит окно нажимаем кнопку Да , и компьютер начнет устанавливать этот инструмент.
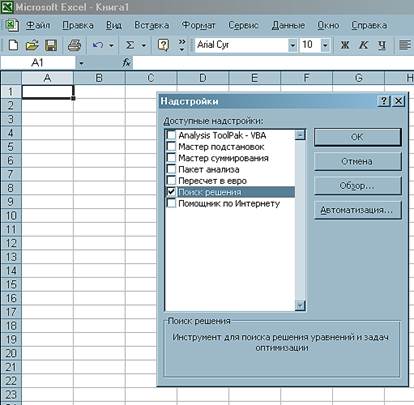
Рисунок 1 – Установка инструмента Поиск решения
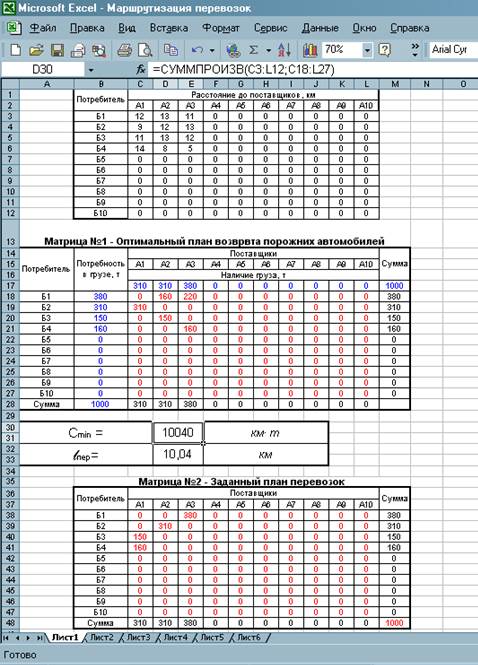
Рисунок 2 – Расстояния до поставщиков, оптимальный и заданный план перевозок
Решение
1. На первом листе размещаем в таблицы (матрица №2) сведения из заказов на перевозку и расстояния от поставщиков к потребителям, как показано на рисунке 2. Находим оптимальный план движения автомобилей без груза (матрица №1), т.е. кратчайший путь возврата порожних автомобилей на пункты погрузки, аналогично тому, как это было сделано ранее при определении оптимального плана закрепления потребителей за поставщиками.
2.Составление алгоритма решения первого маршрута
2.1. Составление совмещенной матрицы (матрица №3)
Накладываем данные одной матрицы на другую, как показано на рисунке 3 . Причем слева в ячейке ставим ссылку на матрицу №2 – план перевозок, а справа в ячейке на матрицу №1 – оптимальный план возврата порожних автомобилей. Например клетка матрицы №3 А1Б1:
– Слева в ячейке С4 листа 2 ставим знак «=», переходим на Лист 1, нажимаем мышкой на ячейку С38, нажимаем Enter, получаем запись в ячейке С4 листа 2:
=Лист1!С38
Это означает что значение в ячейке С4 листа 2 равно значению ячейки С38 листа 1, и если мы поменяем значение в этой ячейке, то автоматически поменяется значение в С4 листа 2.
– Справа в ячейке D4 листа 2 ставим знак «=», переходим на Лист 1, нажимаем мышкой на ячейку С18, нажимаем Enter, получаем запись в ячейке D4 листа 2:
=Лист1!С18
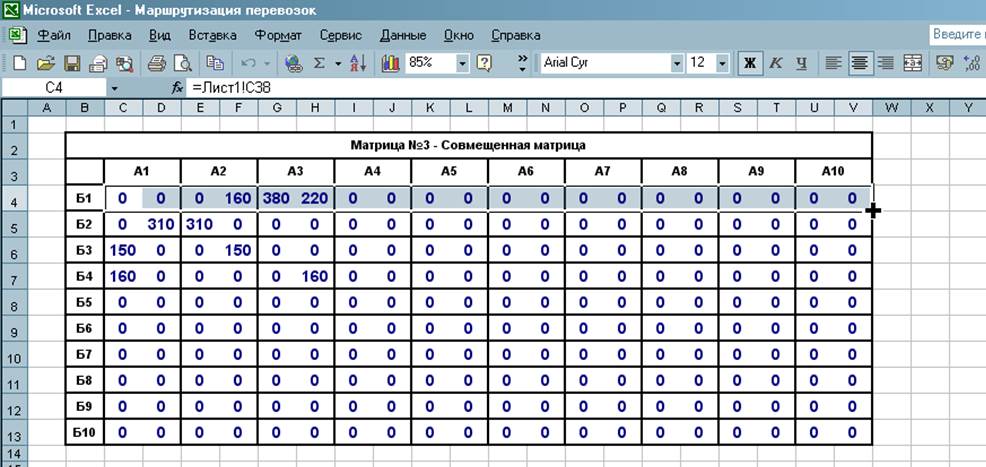
Рисунок 3 – Совмещённая матрица
Так заполняем все ячейки первой строки. Заполнение остальных ячеек делаем так: левой кнопкой мышки выделяем все ячейки первой строки, ставим курсор в левый нижний угол, что бы курсор принял вид «+», нажимаем и держим левую кнопку мыши, ведём мышкой до самой нижней строки, отпускаем кнопку. Таким образом, формулы из ячеек первой строки переносятся на остальные ячейки. Если в клетке матрицы находятся две цифры, то это и есть маятниковый маршрут.
2.2. Расчет маятниковых маршрутов
Для расчета маятниковых маршрутов составляем матрицу №4
(рисунок 4). Что бы выделить маятниковые маршруты нужно вывести минимальное число
из каждой клетки совмещенной матрицы. Для этого нам потребуется функция МИН(число1;число2;…),
она возвращает минимальное значений из
списка аргументов. Для этого в ячейке С17 ставим
знак «=», верхнем правом углу ищем значок fx
, нажимаем его, откроется окно Мастер функций, в поле Категория выбираем
Полный арифметический перечень, ищем функцию МИН, нажимаем ОК, откроется окно Аргументы функции, в строке Число1
нажимаем на значок 
,
мышкой выделяем ячейку С4,
нажимаем Enter, в строке Число2 нажимаем на значок 
, мышкой выделяем ячейки D4, нажимаем Enter, затем ОК, таким образом, мы записываем формулу в ячейке С17:
=МИН(C4;D4)
в ячейке D17 записываем формулу:
=С17
в ячейке E17 записываем формулу:
=МИН(E4;F4)
в ячейке F17 записываем формулу:
=E17
Так заполняем все ячейки первой стоки. Остальные ячейки заполняем, перенося формулы, как это было показано выше, получаем матрицу №4.
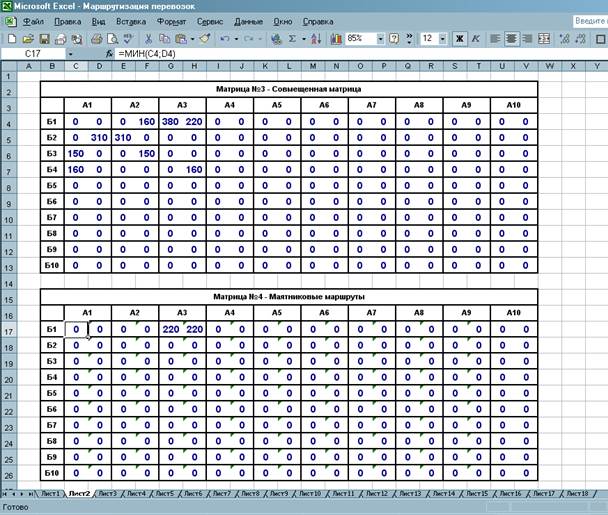
Рисунок 4 – Маятниковые маршруты
Таким образом, матрица №4 отображает количество груза, перевозимое в маятниковых маршрутах. Далее исключаем маятниковые маршруты из совмещенной матрицы. Для этого вычитаем из матрицы №3 матрицу №4 по каждой ячейке (рисунок 5). В ячейке С30 ставим знак «=», мышкой нажимаем на ячейку С4, ставим знак «-», мышкой нажимаем на ячейку С17, получаем запись
=C4-C17
Переносим эту формулу сначала на всю строку, затем на всю матрицу. Таким образом, получаем матрицу №5.
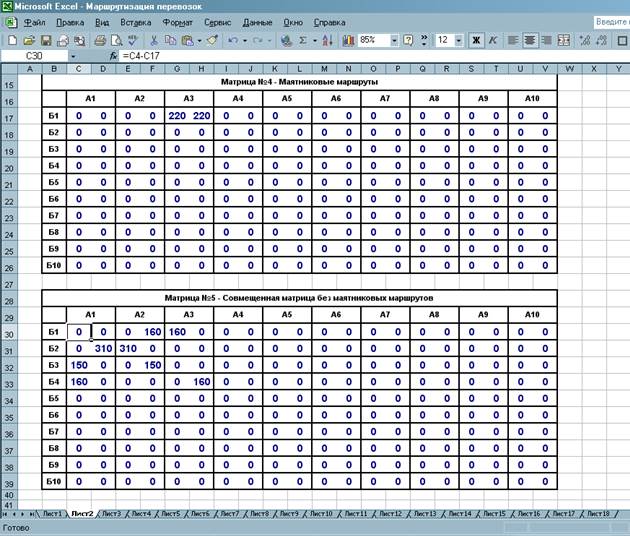
Рисунок 5 – Совмещенная матрица без маятниковых маршрутов
2.3. Составление поля изменяемых ячеек и ограничения для инструмента Поиск решения
Составляем вспомогательную матрицу (рисунок 6). В ячейке С44 записываем формулу
=МАКС(C30;D30)
в ячейке D44 записываем формулу
= МАКС(E30;F30)
Так заполняем первую строку, на остальные строки переносим формулы. Таким образом, получаем матрицу №6.
Находить маршрут будем в двоичной системе, то есть «1» означает вершину контура маршрута в клетке матрицы, «0» означает, что вершины контура в клетке нет. Для того чтобы все цифры вспомогательной матрицы перевести в двоичную систему нам потребуется функция ЗНАК(число). Она возвращает знак числа: 1 – если число положительное, 0 – если оно равно нулю и -1 – если число отрицательное.
Для этого в ячейке N44 записываем формулу:
=ЗНАК(C44)
Переносим формулу сначала на всю строку, а затем на всё матрицу. Таким образом, получаем матрицу №7
Для заданного плана из совмещенной матрицы без маятниковых маршрутов (рисунок 5) берём цифры слева клетки, то есть в ячейке С58 записываем формулу:
=ЗНАК(C30)
в ячейке D58 записываем формулу:
=ЗНАК(E30)
И так, заполняем все ячейки первой строки, затем формулы из первой строки переносим на всю матрицу, получаем матрицу №8.
А для оптимального плана из совмещенной матрицы берём цифры справа клетки, то есть в ячейке N58 записываем формулу:
=ЗНАК(D30)
в ячейке O58 записываем формулу:
=ЗНАК(F30)
Так, заполняем все ячейки первой строки, затем формулы из первой строки переносим на всю матрицу, получаем матрицу №9.
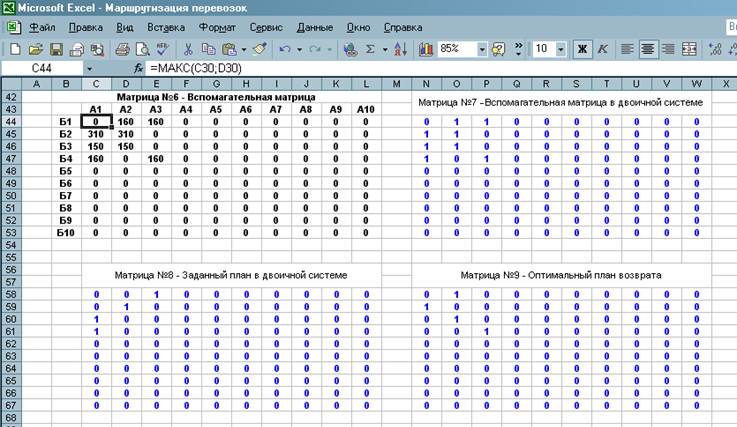
Рисунок 6 – Вспомогательная матрица, заданный план и оптимальный план возврата в двоичной системе
Матрицы №8 и №9 будут являться ограничениями для инструмента Поиск решения.
Составим поле изменяемых ячеек (рисунок 7).
В этом поле программа вычертит контур маршрута, то есть будет ставить в каждой клетке либо «1» либо «0». Чтобы обеспечить чередование цифр из оптимального плана возврата и заданного плана в контуре, поле изменяемых ячеек разбиваем на две половины. Верхняя (ячейки C71;L80) будет отображать вершины контура маршрута из заданного плана, а нижняя (ячейки C81;L90) из оптимального плана возврата.
Раскрываем меню Сервис, открываем инструмент Поиск решения:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.
