Вычисление моментов инерции сложных фигур

Вычисление моментов инерции сложных фигур.

При практических расчетах  различных балок приходится определять моменты инерции сложных поперечных сечений, состоящих из нескольких простых.

Рассмотрим пример определения моментов инерции для фигуры, показанной на     рис.1, состоящей из трех прямоугольников с площадями F₁, F₂, F₃.

Расчет начинается с определения центра тяжести всей фигуры. В качестве начальных осей возьмем оси Z₀ и У₀, показанных на рисунке.

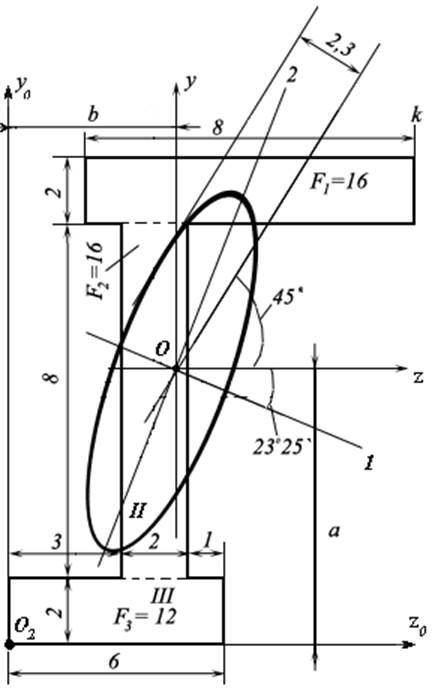
рис.1

Найдем положение центра тяжести по формулам:  ;     ,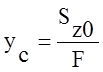

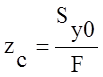 где   S_z0 = S_z1+S_z2+S_z3; F=F₁+F₂+F₃;

   S_z1=F₁у_c1; S_z2=F₂y_c2; S_z3=F₃y_c3.

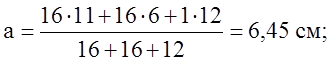
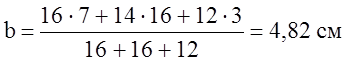
Центральные оси Z и У проходят через точку О  на  расстоянии а и b относительно осей  Z₀ и У₀.

Находим моменты инерции всего сечения относительно центральных осей, применяя формулы параллельного переноса осей:

J_z=J_z1+J_z2+J_z3;    ;    ;    ,

где i – номер простого сечения  i=1,2,3;

а_i и в_i – расстояния от центра тяжести всего сечения до центров фигур;

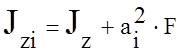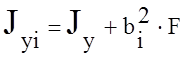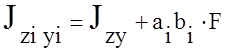J_z, J_y, J_zy – моменты инерции простых сечений.

;

.

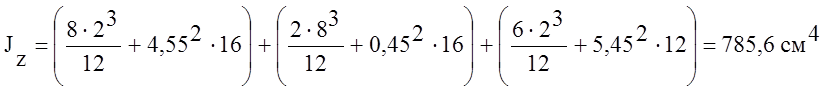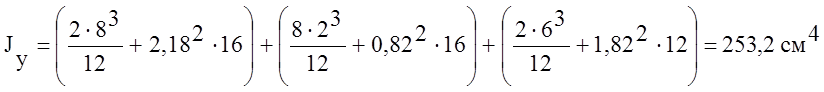          Находим центробежный момент инерции относительно центральных осей:

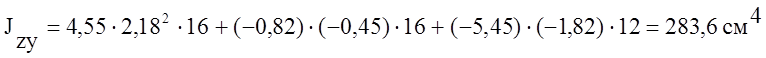
Главные моменты инерции найдем по формулам:

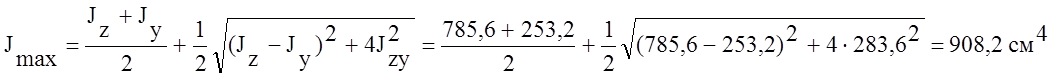
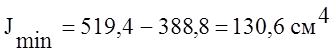, или

Для определения угла наклона главных осей используем формулу: 

,

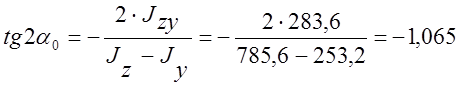следовательно,

Угол  дает положение главной оси 1, относительно которой момент инерции имеет максимальное значение при  и минимальное при

Главные центральные  оси инерции под номерами 1 и 2 показаны на рис.1

Найдем теперь радиусы инерции:

 

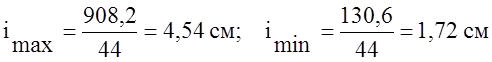
По этим данным построен  эллипс инерции (рис. 1).