Геометрические характеристики плоских сечений.
При изучении растяжения–сжатия установлено, что напряжение и деформация стержня пропорциональны его площади поперечного сечения.
В случае деформации изгиба и кручения оказывается, что площадь поперечного сечения не может характеризовать его сопротивляемость.
Необходимо использовать более сложные геометрические характеристики сечения.
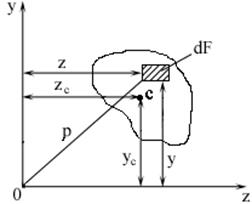 1.
Статический момент площади
1.
Статический момент площади
![]() ;
; 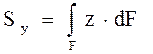 .
.
Статический момент центра тяжести сечения относительно произвольных координатных осей определяется
![]() ;
; ![]() .
.
Из этих выражений можно определить положение центра тяжести.
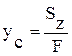 ;
; 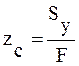 ;
;
Статический момент относительно оси, проходящей через центр тяжести, равен нулю.
2. Осевые моменты инерции поперечного сечения.
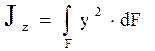 ,
, ![]() .
.
Jz и Jy имеют только положительные значения.
3. Центробежный момент инерции.
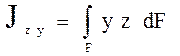 .
.
Центробежный момент инерции может принимать значения Jz y > 0, или Jz y < 0, либо равен 0.
Центробежный момент относительно оси, проходящей через центр тяжести равен 0
4. Полярный момент инерции
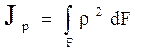 .
.
Так как ![]() , то
, то ![]()
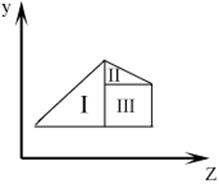
Определение моментов инерции сложного сечения.
 Моменты
инерции сложного сечения равны алгебраической сумме моментов инерции простых
сечений.
Моменты
инерции сложного сечения равны алгебраической сумме моментов инерции простых
сечений.
Для сечения, изображенного на рисунке
![]() ,
, ![]() ,
,
где ![]() ,
, ![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
, ![]() –
моменты инерции простых сечений, составляющих сложное.
–
моменты инерции простых сечений, составляющих сложное.
Моменты инерции простых сечений.
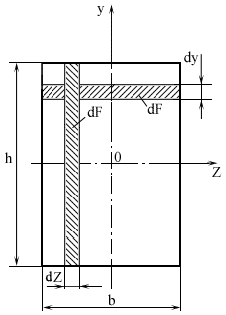
1. Прямоугольное сечение
Момент инерции относительно оси Z
![]()
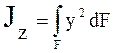 .
.
Выделим
элементарную площадку dF с шириной b и высотой dy, ![]() ;
;
Тогда
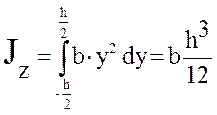 .
.
Для
определения момента инерции относительно оси y выделим
элементарную площадку dF с высотой h и шириной dz , ![]()
 Подставим dF в формулу
Подставим dF в формулу 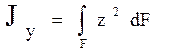 , получим
, получим 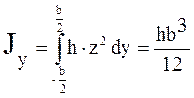 .
.
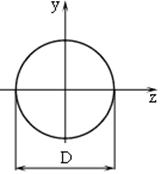
2. Круговое
сечение 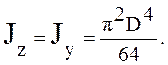
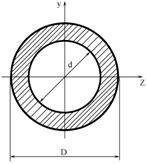
3. Кольцевое сечение
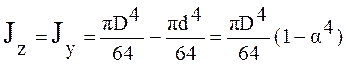 , где
, где 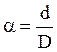 .
.
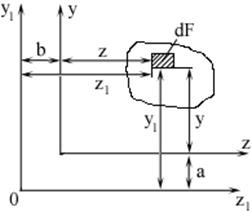
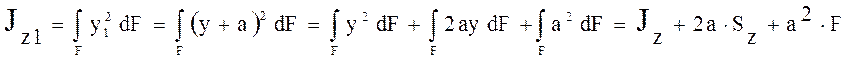 Выведем
Выведем ![]()
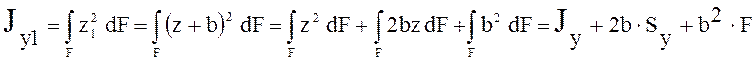
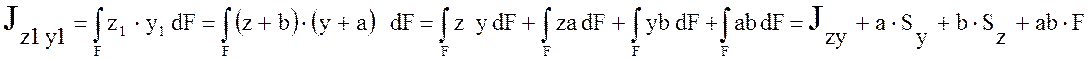 В случае, когда ось проходит через
центр тяжести поперечного сечения
В случае, когда ось проходит через
центр тяжести поперечного сечения 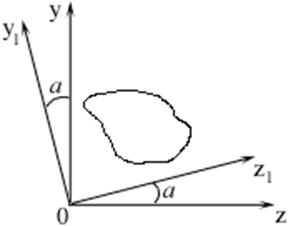
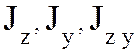 моменты
инерции
моменты
инерции 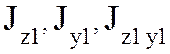 относительно повернутых осей
относительно повернутых осей 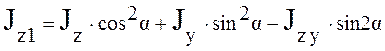
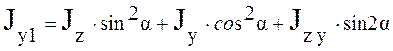
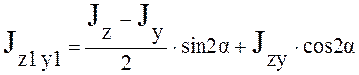
Система координат относительно, которой осевые моменты инерции имеют экстремальные значения, называется главной системой, а моменты инерции относительно этих осей, называются главными осевыми моментами инерции.
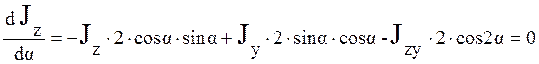 Определим угол поворота главных осей относительно центральных осей. По
правилу существования экстремума
Определим угол поворота главных осей относительно центральных осей. По
правилу существования экстремума
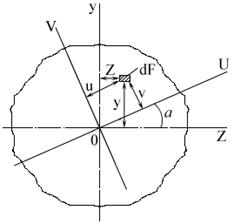
После преобразования
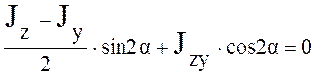
Полученная формула является формулой центробежного момента,
следовательно 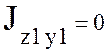 , и оси
являются главными.
, и оси
являются главными.
Разделим 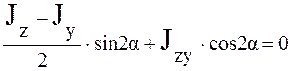 на
на ![]() , тогда
, тогда 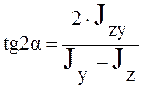
Формула для
определения положения главных осей имеет вид: 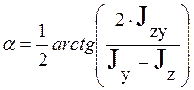
Подставим угол a в предыдущие формулы ![]() , найдем главные
моменты инерции
, найдем главные
моменты инерции
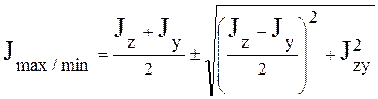
Свойство. Центробежный момент инерции для любой оси симметрии равен 0, т.е. любая ось симметрии является главной.
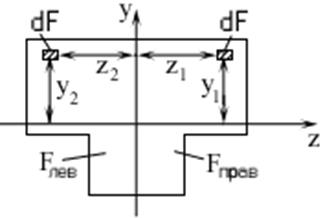 Центробежный
момент составного сечения, приведенного на рисунке, можно выразить:
Центробежный
момент составного сечения, приведенного на рисунке, можно выразить:
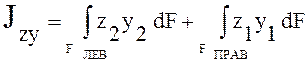
Точка А1
имеет координаты у1 и z1 на Fправ, ввиду симметрии сечения относительно оси У Fлев = Fправ и
найдется точка А2 для которой выполняются условия: ![]() .
.
Тогда 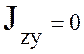 и следовательно ось симметрии У
является главной. Таким образом, для симметричных фигур главные оси
устанавливаются без вычислений. Одна ось совмещается с осью симметрии, а другая
проводится перпендикулярно ей. Особое значение имеют главные оси, которые
проходят через центр тяжести. Такие оси называются главными центральными
осями.
и следовательно ось симметрии У
является главной. Таким образом, для симметричных фигур главные оси
устанавливаются без вычислений. Одна ось совмещается с осью симметрии, а другая
проводится перпендикулярно ей. Особое значение имеют главные оси, которые
проходят через центр тяжести. Такие оси называются главными центральными
осями.
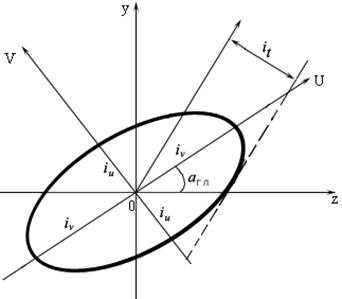
Эллипс инерции позволяет
графически определить момент инерции относительно любой оси, проходящей через
начало координат, например, относительно оси t. На
рисунке оси У и Z –центральные, оси U
и V – главные. Известны моменты ![]() .
.
Определим радиусы инерции: 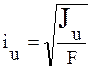 ,
, 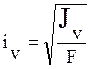 .
.
При построении эллипса по оси U откладываем радиус iv , по оси V – радиус iu.
Уравнение эллипса имеет вид:
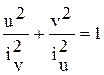
Для определения Jt проводим касательную параллельную оси t.
Момент инерции 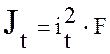 ,где it
– расстояние между осью t и касательной.
,где it
– расстояние между осью t и касательной.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.