Анализ воздействия отклонения напряжения на процесс теплового износа изоляции электродвигателя АНЭ-225L4УХЛ2, страница 3

где    τ₁ и τ₂ – превышение температуры соответственно обмотки и стали над температурой окружающей среды, ^оС;

α – температурный коэффициент сопротивления материала проводника обмотки, 1/^оС.

Перепишем уравнения в операторной форме

(рС₁ + Л₁ + Л₁₂ – αР₁₀)τ₁ – Л₁₂τ₁₂=Р₁₀/р ,         (56)

-Л₁₂τ₁ + (рС₂ +Л₂ + Л₁₂)τ₂=Р₂/р ,                (57)

Решив систему уравнений, найдем превышение температуры обмотки в операторной форме

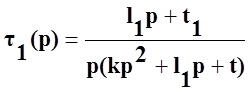 ,                     (58)

где                                                     l₁=C₂∙P₁₀ ,                            (59)

t₁=P₁₀(Л₂ + Л₁) = Л₁₂∙Р₂ ,                  (60)

к=С₁∙С₂ ,                                 (61)

е=С₁(Л₂ + Л₁₂) + С₂(Л₁ + Л₁₂ -α∙Р₁₀) ,           (62)

t=(Л₁ + Л₁₂ - α∙Р₁₀)∙(Л₂ + Л₁₂) – Л₁₂² .          (63)

Обозначим

F₁(p)=l₁∙p + t₁  ,                               (64)

F₂(p)=k∙p² + l∙p + t .                          (65)

Перепишем уравнение с учетом введенных обозначений

τ₁(р)=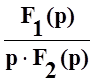 .                                 (66)

Уравнение F₂(p)=0 имеет два различных и не равных нулю корня – р₁ и р₂, поэтому

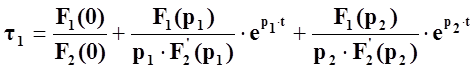 ,           (67)

где

F^’₂(p)=2∙к∙р + 1.                                (68)

Выведем формулу установившегося превышения температуры обмотки асинхронного электродвигателя.

при t=∞ получаем

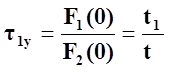 ,                                (69)

Подставив значения t₁ и t , получаем

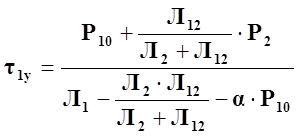 ,              (70)

Р₁₀=3∙r₀∙I² ,                                (71)

где   r₀ – сопротивление обмотки при температуре окружающей среды, Ом;

I – ток, потребляемый электродвигателем, А.

Введем обозначения

 ,

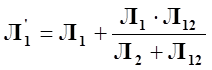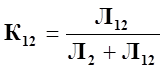 ,(32) ,                     (72)

перепишем уравнение (117)

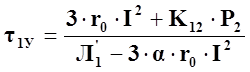 .                       (73)

При нагрузке, отличной от номинальной, I=кI_н. Подставив это значение тока в (73) и преобразовав, получим следующее выражение для определения установившегося превышения температуры обмотки электродвигателя в функции кратности тока нагрузки по отношению к его номинальному значению

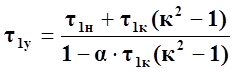                                      .                          (74)

Найдем способ определения значения τ_1к по паспортным данным электродвигателя, рассуждая следующим образом: в номинальном режиме работы превышение температуры обмотки также будет номинальным и может быть найдено по выражению

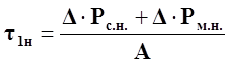,                           (75)

где  ∆Р_с.н. и ∆Р_м.н. – номинальные потери соответственно в стали и меди электродвигателя, Вт;

А – эквивалентная теплоотдача обмотки, Дж/с^оС.

В опыте короткого замыкания это уравнение приобретает вид

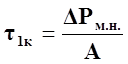 .                              (76)

Решая совместно уравнения, находим

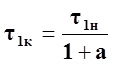                                                ,                                 (77)

где

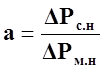                                                 ,                                  (78)

Подставив, получаем

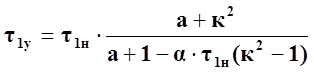                                       .              (79)

Таким образом, установившееся превышение температуры обмотки зависит от кратности тока электродвигателя, коэффициента потерь и материала проводника, которому соответствует температурный коэффициент сопротивления α.

Заменив реальную кривую нагрева обмотки электродвигателя эквивалентной кривой, получим уравнение нагрева обмотки

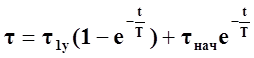 ,               (80)

где τ_нач – начальное значение превышения температуры обмотки, ^оС;

Т – эквивалентная постоянная времени нагрева электродвигателя, мин;

t – текущее время, мин.

Эквивалентная постоянная времени нагрева электродвигателя может быть найдена по выражению

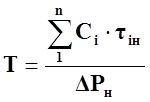 ,                   (81)

где С_i – теплоемкость i-го тела электродвигателя, Дж/^оС;

τ_iн – превышение температуры i-го тела электродвигателя в номинальном режиме работы последнего, ^оС;

     ∆Р_н – номинальные потери мощности, Вт.

3.3 Расчет воздействия отклонения напряжения на процесс теплового износа изоляции электродвигателя АНЭ-225L4УХЛ2.

3.3.1 Расчет значения превышения температуры при номинальной мощности на валу двигателя P=55кВт.

Рабочие характеристики показаны на рисунке 3.3

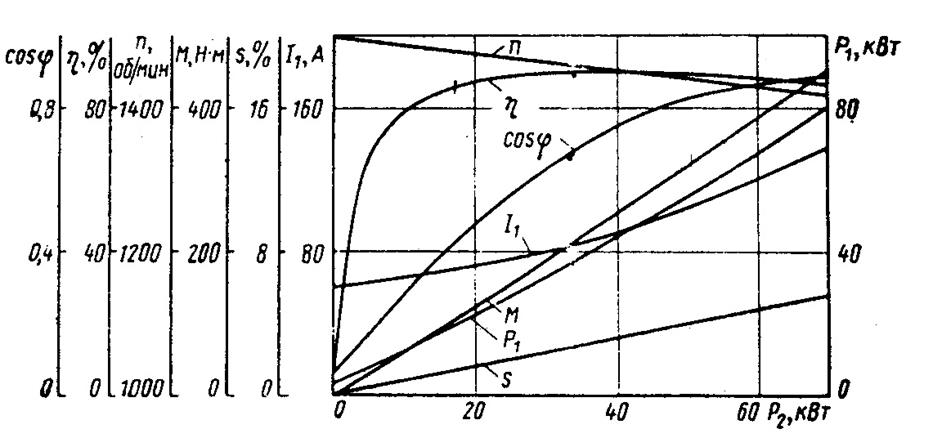
Рисунок 3.3-  Рабочие характеристики электродвигателя АНЭ-225L4УХЛ2

Эквивалентная постоянная времени нагревания электродвигателя находится по формуле:

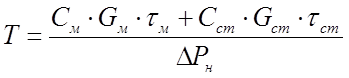,                (82)

где -превышение температуры меди в номинальном режиме работы,

- масса меди,

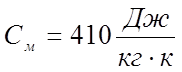- удельная теплоемкость меди,

-превышение температуры стали в номинальном режиме работы,

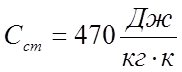- удельная теплоемкость стали.

- номинальные потери мощности в электродвигателе найдем по формуле:

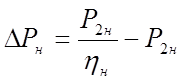,                  (83)

где - номинальная мощность на валу двигателя,

- номинальный коэффициент полезного действия,

,

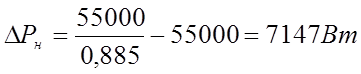подставляя значения в формулу (82) получим:

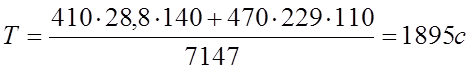
Установившееся превышение температуры определим по формуле:

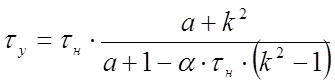,                 (84)

где -начальное превышение температуры,

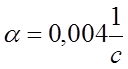- температурный коэффициент сопротивления материала проводника,

- коэффициент потерь,

- кратность тока находим из выражения:

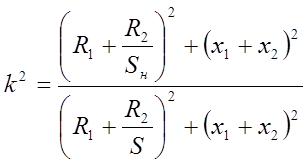,                    (85)

где - параметры схемы замещения,

- скольжение находим по формуле:

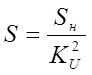,                            (86)

где - номинальное скольжение,

- кратность напряжения на зажимах электродвигателя.

Максимальное превышение температуры рассчитывается по формуле:

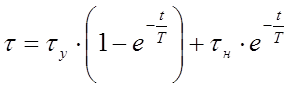,              (87)

Проведем расчет при значении напряжения на токоприемнике Uэ=18кВ.

При Uэ=18кВ напряжение U1=250В.

Найдем кратность напряжения на зажимах электродвигателя:

;

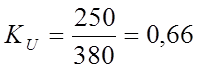Найдем скольжение:

;

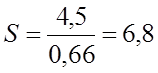Найдем кратность тока:

;

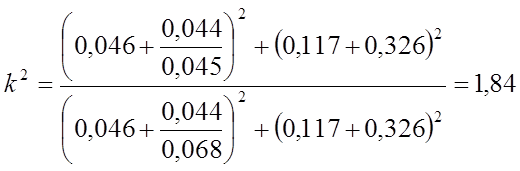Найдем установившееся превышение температуры:

;

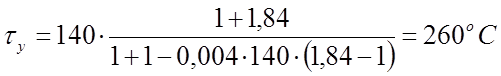Найдем максимальное превышение температуры:

;

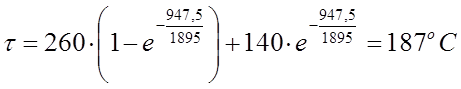Далее расчет производим аналогично, используя время t в интервале от 0 до 1895с. с шагом 190с.

Результаты расчетов сведем в таблицу 3.3

Таблица 3.3- Результаты расчета превышения температуры при различном значении напряжения на токоприемнике.