Анализ воздействия отклонения напряжения на процесс теплового износа изоляции электродвигателя АНЭ-225L4УХЛ2, страница 2

    В эксплуатации в системах вспомогательных машин асинхронных электродвигатели питают несинусоидальным несимметричным напряжением, изменяющимся в широких приделах. При этом токи обмоток фаз статора могут отличаться в несколько раз; в машине существуют магнитные поля, вращающиеся и в прямом и обратных направлениях; в роторе протекают соизмеримые по величине токи частот в несколько герц и около 100 Гц. Потери энергии и их распределение в машине при этом коренным образом отличается от того, что свойственно номинальному режиму при симметричном питании.

    Если вспомогательные машины выбраны с запасом мощности по условию пуска при пониженном напряжение, то обычно их превышение температур не превышают норму для наибольших не симметрий токов. Однако указанные проверки теплового состояния во всех случаях необходимы.

3.2 Расчет установившегося превышения температуры обмотки асинхронного двигателя по методике, предложенной Овчаровым В.В.

Рассмотрим методику, предложенную Овчаровым В.В.

Среди различных факторов, определяющих срок службы изоляции электрических машин, одним из основных является тепловое старение. При анализе эксплуатационных режимов особое значение приобретают методы расчета скорости теплового старения электрической изоляции и определение срока её службы.

Первые работы в этом направлении имели преимущественно экспериментальный характер и относились главным образом к изоляции класса А. В результате было сформулировано так называемое правило «восьми градусов», в соответствии с которым повышение температуры изоляции на каждые восемь градусов сокращает срок её службы вдвое. Аналитически это правило выражается в виде уравнения

Д=Д₀ е^-0,0866θ,                                       (41)

где Д₀ – срок службы изоляции при температуре 0 ⁰С, ч;

θ – температура изоляции, ⁰С.

Правило «восьми градусов» вследствие своей простаты находит широкое применение и позволяет производить ориентировочные расчеты в тех случаях, когда они относится к сравнительно небольшим диапазонам изменения температуры. Недостаток уравнения (88) является его эмпирический и формальный характер, что вносит неопределенность в значения числовых постоянных и не позволяет рассчитывать на получение этим методом достаточно надежных результатов.

Более строгим подходом к исследованию явлений старения изоляции заключается в применении к ним общих законов кинетики химической реакции. Я. Вант Гоффом и С. Аррениусом было найдена зависимость скорости химических реакций от температуры

lnK=B/Θ+A,                                        (42)

где  К – постоянная скорость реакции;

Θ – абсолютная температура, ⁰К;

В и А – постоянные коэффициенты.

Экспериментально доказано, что окислительный процессы, происходящие в изоляции, относится к классу мономолекулярных реакций, для которых справедливо уравнение

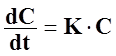,                                           (43)

где С – концентрация не прореагировавших молекул в рассматриваемый момент времени t.

Из уравнения (43) следует

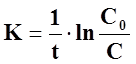 ,                                       (44)

где С₀  - начальная концентрация не прореагировавших молекул.

Коэффициенты А и В имеют определенный физический смысл и связаны с постоянными, характеризующими химический состав и структуру вещества, участвующего в реакции, соотношениями:

А=ln(PZ) ,                                 (45)

P=e^∆S/R ,                                     (46)

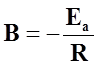 ,                                  (47)

где  Z – число столкновений между реагирующими молекулами в единицу времени;

Р – фактор вероятности надлежащей ориентации молекул при столкновении;

∆S – энтропия активации – величина, характеризующая долю общего числа столкновений, при которых молекулы ориентированы надлежащим образом;  

R=8,317 – универсальная газовая постоянная;

Е_а – энергия активации, т.е. избыточное (по сравнению со средней величиной) количество энергии, которым должна обладать молекула, чтобы преодолеть энергетический барьер и оказаться способной к данному химическому взаимодействию.

Объединяя приведенные выше уравнения, можно получить уравнение Вант Гоффа – Аррениуса

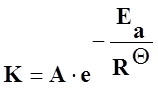 ,                          (48)

Таблица 3.2- Значения В для различных изоляционных материалов

Класс изоляции	В, К	Θн ,К	Дн ,бч	G
А	9500	378	20000	15,3
В	9850	393	20000	1,1
H	10200	403	20000	1,5
F	12700	428	20000	1,7

Решая совместно уравнения и обозначая срок службы изоляции через Д, получим

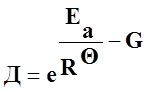 ,                           (49)

где

G=lnA-lnln.                         (50)

Зная срок службы изоляции Д_н при температуре Θ_н, можно найти срок службы изоляции Д при температуре Θ

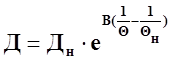 .                        (51)

Найдем скорость теплового износа изоляции (в базовых часах за час) при заданной её температуре

ε= ,                                    (52)

где    Д_н – базовый ресурс изоляции, бч:

Д – срок службы изоляции при температуре Θ, ч.

Подставив значения Д , получим

ε=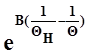  .                             (53)

Асинхронный двигатель с точки зрения его нагрева с достаточной степенью точности можно рассматриваться как система двух тел – обмотки и стали (рисунок 3.2). Тело 1 и 2 (обмотка и сталь) обладают теплоемкостями С₁ и С₂ и связаны между собой тепловой проводимостью Л₁₂, а с окружающей средой тепловыми проводимостями Л₁ и Л₂ . В теле 1 выделяются потери Р₁, в теле 2 - потери Р₂. Предполагается, что теплоёмкости и тепловые проводимости не зависят от температуры, теплоёмкость окружающей среды С_ср, равна бесконечности, температура окружающей среды ν_ср постоянна. 

Рисунок 3.2- Тепловая схема замещения асинхронного электродвигателя

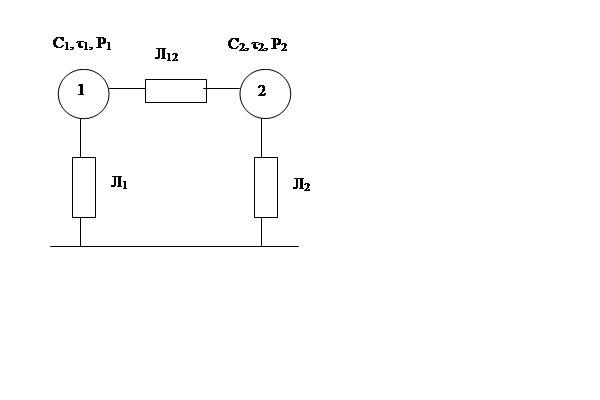
Составим уравнения теплового баланса для каждого тела обмотки (тело1) и стали (тело2)

Р₁₀(1+α∙τ₁)dt=C₁dτ₁+Л₁τ₁dt+Л₁₂(τ₁-τ₂)dt ,           (54)

Р₂dt + Л₁₂(τ₁ - τ ₂)dt=C₂dτ₂ + Л₂τ₂dt ,           (55)