

Дифференциальные зависимости между MX, QY и q
(дифференциальные зависимости Журавского Д.И.)
Между внешней нагрузкой, в частности интенсивностью распределенной нагрузки qyпоперечной силой Qyи изгибающим моментом Мzимеются важные дифференциальные зависимости, которые часто будут использоваться в дальнейшем.
Рассмотрим балку с внешней распределенной нагрузкой q, направленной вниз вдоль оси у (рис. 1, а). Такую нагрузку будем считать положительной. Выделим из нее в произвольном месте элемент длиной dх и рассмотрим его.
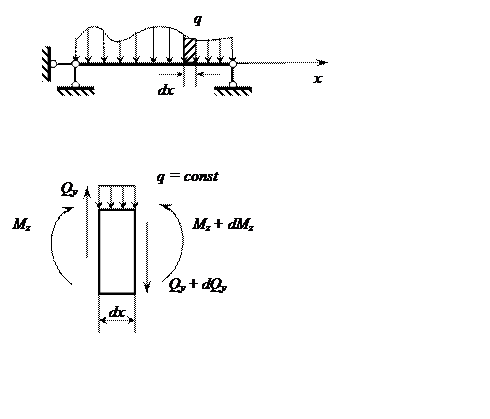 |
Действие левой отброшенной части балки на элемент заменим поперечной силой Qyи изгибающим моментом Мz, а действие правой отброшенной части — силой Qy+dQyи моментом Мz+ +dMz,. Здесь dQyadMz— приращение поперечной силы и изгибающего момента на элементе dx. Предположим что поперечные силы и изгибающие моменты положительны. Кроме этих сил на элемент действует внешняя распределенная нагрузка q, которую вследствие малости dx можно считать равномерно распределенной. Под действием указанных сил элемент находится в равновесии.
Составим уравнение проекций сил на ось y
![]()
Преобразуем уравнение
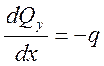
Первая производная от поперечной силы по продольной координате х равна интенсивности распределенной нагрузки, взятой с обратным знаком.
Составим уравнение моментов для участка dx относительно правого сечения
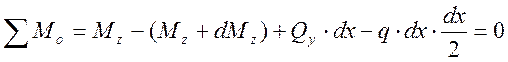
В этом уравнении 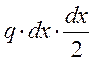 - величина, которой пренебрегаем вследствие
ее малости. В соответствии с этим
- величина, которой пренебрегаем вследствие
ее малости. В соответствии с этим 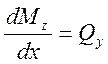
Первая производная от изгибающего момента по продольной координате х равна поперечной силе.
Вторая производная от изгибающего момента по продольной координате х равна интенсивности распределенной нагрузки, взятой с обратным знаком.
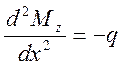
На основании полученных дифференциальных зависимостей можно сформулировать ряд основных положений, оказывающих помощь при построении эпюр поперечных сил и изгибающих моментов и позволяющих выполнять проверку правильности их построения.
1. На участке, где нет распределенной нагрузки, поперечная
сила постоянна Q, изгибающий момент М изменяется по линейной
зависимости (причем тангенс угла наклона а эпюры М равен силе Q), т.е.
если q = 0, следовательно 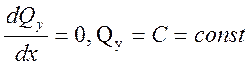 .
.
Если 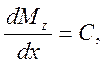 то после
интегрирования получим Mz = Cx + D- уравнение прямой линии.
то после
интегрирования получим Mz = Cx + D- уравнение прямой линии.
В частном случае одновременно может быть q = 0 а Q = 0, тогда изгибающий момент М постоянен.
2. На участке, где имеется равномерно распределенная нагрузка, поперечная сила изменяется по линейной зависимости (тангенс угла наклона β эпюры Q равен q), а изгибающий момент — по квадратичной зависимости, у которой выпуклость обращена в сторону действия распределенной нагрузки q.
3. Если участке балки поперечная сила в одном из сечений равна нулю (Q = 0), то изгибающий момент в этом сечении принимает экстремальное значение Mэкстр — максимум или минимум.
4. Если участке балки значение поперечной силы положительно (Q > 0), то ординаты эпюры изгибающих моментов M возрастают.
Если участке балки значение поперечной силы отрицательно (Q < 0), то ординаты эпюры изгибающих моментов M убывают.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.