Количественный рентгенофазовый анализ: Методические указания к лабораторным работам, страница 4

              На заключительном этапе ФИ из отобранных фаз, тем или иным способом,  строится модельный спектр идентифицируемого образца. Модельный спектр определяется как сумма эталонных спектров I_i^эт(2Θ_j), умноженных на масштабные коэффициенты С_i^усл:

(10)

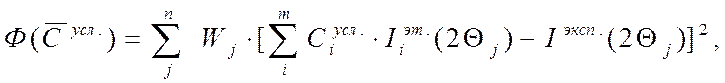               При этом условные концентрации рассчитываются по МНК из условия максимального совпадения модельного спектра с экспериментальным:

где I_i^эт(2θ_j) – полный эталонный спектр i-й фазы,  С_i^усл -  масштабный коэффициент (условная концентрация) вхождения эталонного спектра  i-й фазы в рентгенограмму, W_j– весовая схема.

            Поскольку в БД [6]  накоплено свыше 200 тысяч  рентгенофазовых эталонов, а спектры фаз материала, как правило, не вполне совпадают с рентгенофазовыми эталонами из-за различий в реальной кристаллической и микрокристаллической структуре фаз, перед началом идентификации предпочтительно создавать выборку только тех эталонов, фазы которых соответствуют химическому элементному составу анализируемых материалов.

Метод корундовых чисел

             Вариантом КРФА не требующим непосредственного эталонирования является использование корундовых чисел фаз (RIR метод) [7,8].  Корундовые числа (отношение интенсивностей максимальных линий фазы и корунда в смеси 1:1) накапливаются в базах данных вместе с рентгеновскими стандартами фаз.

               Из (9) и определения корундового числа следует:

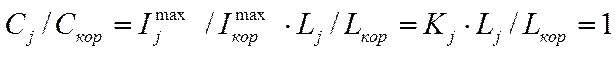          ,                      (11)

где К_j– корундовое число фазы j. 

                Из (8) также следует, что корундовое число можно выразить через калибровочные коэффициенты  L_j  фазы j и  L_кор корунда: 

                                                 .                                                 (12)

Имеется три варианта данного метода.

             Первый основан на использовании внутреннего эталона, в этом случае производя преобразование аналогично (11) имеем:

.

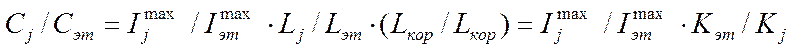            Откуда концентрации фаз вычисляются через измеренные интенсивности, корундовые числа фаз и эталона и известной концентрации фазы эталона, по формуле:

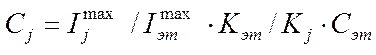                       .                                            (13)

           Достоинством варианта является возможность анализа без какой-либо калибровки и, даже, в присутствии аморфной фазы, причем содержание последней можно определить из фазового баланса. Недостатком – необходимость подмешивания в пробу фазы внутреннего эталона.

          Второй вариант, называемый нормализованным методом корундовых чисел, основан на использовании фазового баланса, что возможно при отсутствии аморфной фазы. Поскольку из (8) следует:

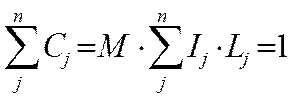                                   ,                                                 (14)

то разделив левые и правые части (8) соответственно на левые и правые части (14) имеем:

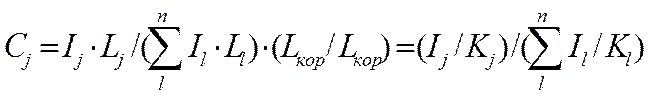                 .                  (15)

          Достоинством варианта является прямое вычисление фазовых концентраций непосредственно из интенсивностей и корундовых чисел, без какой-либо дополнительной информации (без подмешивания или калибровок). Существенным недостатком – необходимость использования интенсивностей максимальных линий, либо, в случае перекрытия максимумов с линиями других фаз, приведения интенсивности аналитических линий к максимальным. Последнее возможно при использовании эталонных спектров БД, в которых приведены относительные интенсивности (в процентах к максимуму). Однако из-за вышеупомянутых различий в структуре фаз или текстуры такой пересчет интенсивности может оказаться весьма неточным и приведет к существенному снижению точности.

           Третий  вариант метода корундовых чисел (автор И.С. Якимов) [9], исключающий отмеченные выше недостатки двух других вариантов метода, является модификация  нормализованного метода корундовых чисел с вовлечением в анализ, вместо интенсивностей отдельных линий, средних характеристик распределения интенсивности полных спектров фаз. Очевидно, таковыми являются условные концентрации фаз, определяемые по МНК при построении модельного спектра по уравнению (10) на этапе качественного фазового анализа. Оказалось, что выражение  (15) можно преобразовать к следующей формуле для вычисления концентрации фаз через условные концентрации фаз и их корундовые числа:

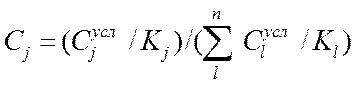                                      .                         (16)

           Достоинством данного варианта является совмещение качественного и количественного фазового анализа, выполняемого одновременно с построением модельного спектра, совпадение которого с экспериментальным является теперь главным критерием достоверности уже не только качественного, но и количественного фазового анализа. Разумеется, при отборе в процессе фазовой идентификации эталонных спектров «истинных» фаз и использовании адекватных корундовых чисел. Последнее требует отдельного обсуждения, однако следует отметить, практика показала, что использование теоретически рассчитанных  корундовых чисел (имеющихся в БД для ~ 50% спектров) приводит, как правило, к весьма точным результатам анализа.

ПМО метода корундовых чисел

              ИПС ФИ - информационно-поисковая система (автор И.С. Якимов)  предназначена для определения качественного и количественного вещественного фазового состава различных многокомпонентных поликристаллических образцов по их экспериментальным рентгеновским дифракционным спектрам (дифрактограммам) с помощью базы данных (БД) рентгенофазовых стандартов (эталонных спектров чистых фаз).