Модифицированные дипольные моменты при взаимодействии двух частиц
В настоящее время становится все более очевидным, что в ближайшие десятилетия одно из основных направлений фундаментальных и прикладных исследований будет связано с разработкой методов создания наноразмерных систем, изучением свойств, и различных применений сверхминиатюрных устройств на их основе. Широкие перспективы создания элементов наноразмерных устройств, и связанный с ними большой интерес исследователей вызывают явления самоорганизации, под действием сочетания сильных и слабых межмолекулярных взаимодействий, зависящих как от структуры конкретных молекул, так и от окружающей их среды (донорно-акцепторных, ван-дер-ваальсовых и т.п.) и теплового броуновского движения. Стратегия, основанная на самоорганизации, является естественной для органической химии и основной в живой природе. В этой связи представляется перспективным использование физических воздействий, и в частности лазерного излучения, для управляемой самоорганизации нано объектов в кластеры, свойства которых можно задавать в процессе их конструирования.
Воздействие лазерного излучения на атомы, молекулы и другие микрочастицы вызывает их поляризацию, которая, с одной стороны, взаимодействуя с лазерным излучением, является причиной возникновения так называемых радиационных сил, позволяющих управлять движением частиц и формировать структуры с размерами порядка длины волны .
С другой стороны, наведенная лазерным излучением поляризация частиц приводит так же и к межчастичному взаимодействию, в том случае, если расстояние между частицами значительно меньше длины волны, что может быть интерпретировано как эффект ближнего поля. Это позволяет формировать уже наноразмерные структуры, с размерами значительно меньшими, чем длина волны лазерного излучения, вызываемого поляризацию.
В большинстве работ, посвященных вопросу взаимодействия частиц в поле, в качестве таких объектов рассматриваются атомы с частотой перехода близкой к резонансу с частотой лазерного излучения. В первой части настоящей лекции рассматривается возможность формирования наноструктур с заданной топологией из металлических наночастиц при их самоорганизации, обусловленной электродинамическим взаимодействием во внешнем поле резонансного лазерного излучения. Вторая часть лекции посвящена формированию микроструктур из наночастиц металлов, обусловленному их электродинамическим взаимодействием с пространственно неоднородным полем.
1. Модифицированные дипольные моменты при взаимодействии двух частиц
В лекции №5 были в общем виде рассмотрены процессы электромагнитного взаимодействия частиц в поле лазерного излучения В этом разделе будет рассмотрен простейший случай, взаимодействие двух одинаковых сферических наночастиц серебра с радиусом Rи расстоянием между ними r12 º r (см. рис. 7.1). Поляризация внешнего светового поля направлена под углом a к прямой, соединяющей центры двух частиц и параллельной оси х.
 |
Тогда проекции на оси xиy поля (см. 5.10 – 5.11) от диполя 1-ой частицы с учетом места расположения 2-ой частицы будут иметь вид
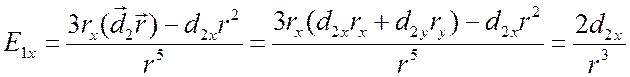
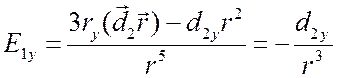 .
(7.1)
.
(7.1)
аналогично,
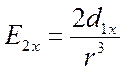 ,
, 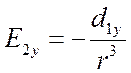 .
.
Тогда, согласно (5.10 – 5.11) получаем систему для нахождения дипольных моментов частиц
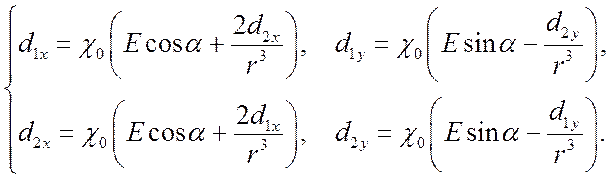 (7.2)
(7.2)
Переписывая систему (7.2) в матричной форме, получим
 . (7.3)
. (7.3)
Очевидно, что эта система распадается на два уравнения, для х и для y-компонент дипольных моментов, и решение (7.3) имеет вид
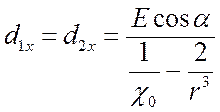 ,
, 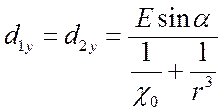 . (7.4)
. (7.4)
Видно,
что при ![]() , то есть в случае изолированных
частиц, формулы (7.4) можно переписать как
, то есть в случае изолированных
частиц, формулы (7.4) можно переписать как ![]() .
Подставляя c0 из (5.14) и
вводя обозначение частоты сдвига:
.
Подставляя c0 из (5.14) и
вводя обозначение частоты сдвига:
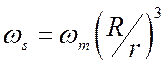 ,
(7.5)
,
(7.5)
можно записать выражения (3.10) в виде
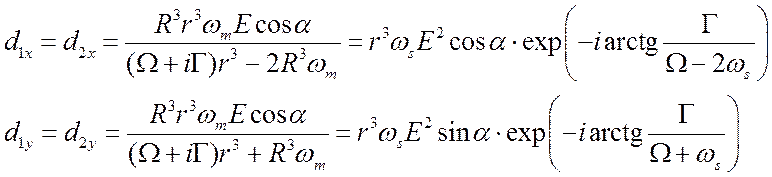 . (7.6)
. (7.6)
2. Энергия взаимодействий частиц
Выведем выражение для энергии диполей двух частиц во внешнем поле
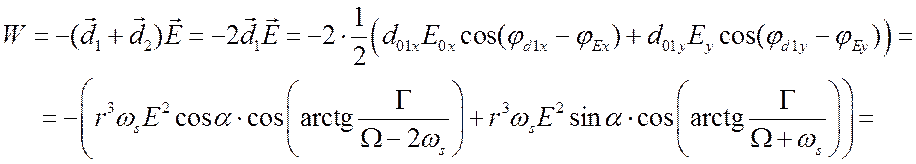
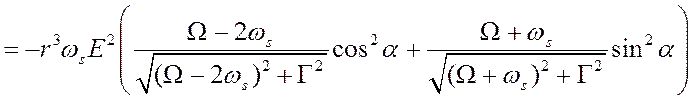 .
.
(7.7)
Таким образом, в результате взаимодействия двух
частиц, их резонансная частота смещается, причём если поле направлено вдоль
пары этих частиц (a= 0),
то резонансная частота определяется условием ![]() ,
то есть уменьшается на
,
то есть уменьшается на ![]() , а если поле ортогонально
частицам – то резонансная частота (
, а если поле ортогонально
частицам – то резонансная частота (![]() ) увеличивается
на
) увеличивается
на ![]() .
.
3. Численный анализ спектров поглощения и энергии взаимодействия пары частиц
Для иллюстрации соотношений (7.6, 7.7) ниже
приведены несколько зависимостей В расчетах принимались следующие значения
входящих в уравнения величин: радиус частиц ![]() нм,
внешнее поле
нм,
внешнее поле ![]() ед. СГС,
температура
ед. СГС,
температура ![]() К, расстояние между частицами
К, расстояние между частицами ![]() нм. Спектры поглощения,
соответствующие мнимой части восприимчивости для взаимно перпендикулярных
компонент поля
нм. Спектры поглощения,
соответствующие мнимой части восприимчивости для взаимно перпендикулярных
компонент поля
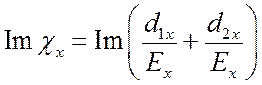 и
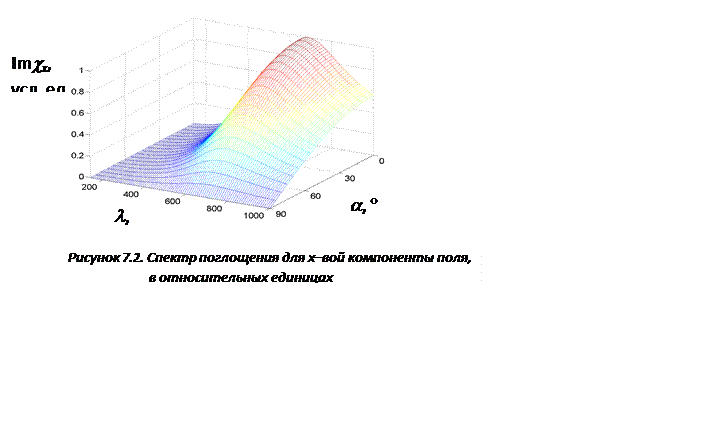
и 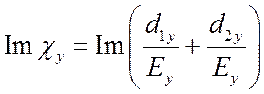 представлены
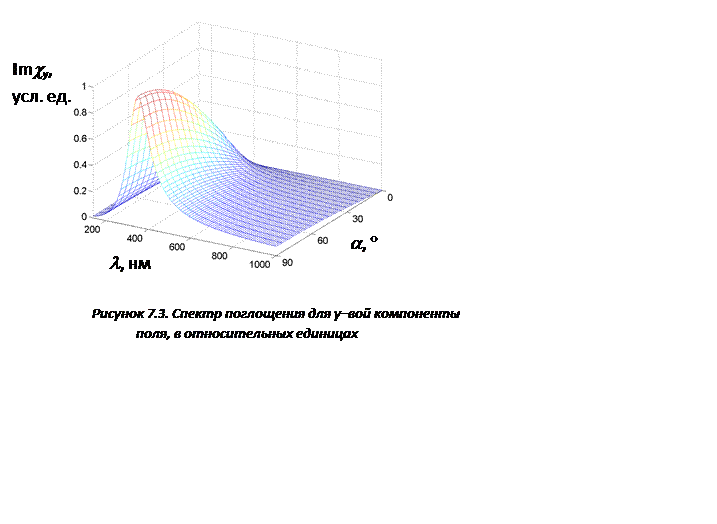
на рис. 7.2 и 7.3.
представлены
на рис. 7.2 и 7.3.
 |
|||
 |
|||
Резонансные длины волн составляют примерно 350 нм для ортогональной ориентации плоскости поляризации, относительно прямой, соединяющей центры частиц, и 710 нм, для параллельной.
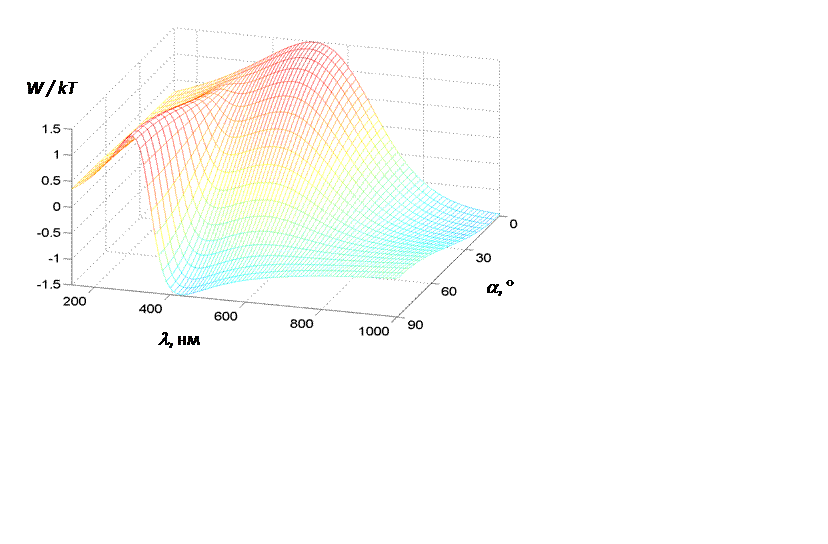 |
Рис. 7.4. Зависимость энергии взаимодействия в относительных единицах.

|
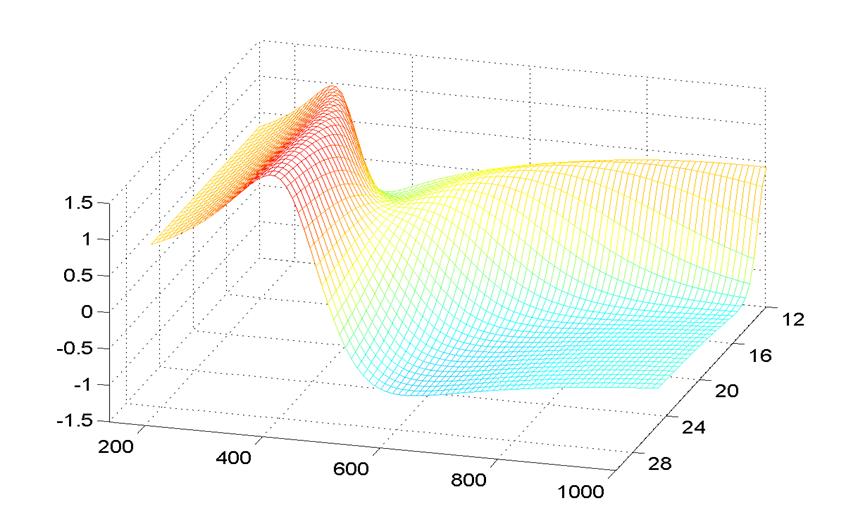 |
Рис. 7.5.
 При
расстоянии между частицами
При
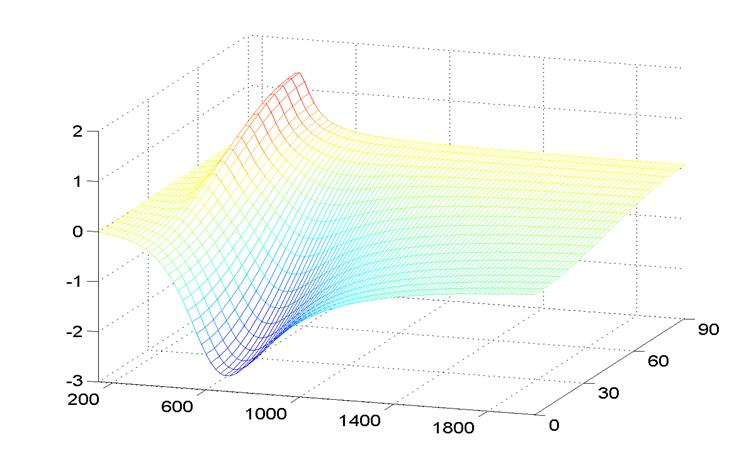
расстоянии между частицами ![]() нм зависимость их
диполь-дипольного взаимодействия от длины волны и направления поля представлена
на рис. 7.6. Глубокая потенциальная яма соответствует
нм зависимость их
диполь-дипольного взаимодействия от длины волны и направления поля представлена
на рис. 7.6. Глубокая потенциальная яма соответствует ![]() °
и
°
и
 |
|
Рис.7.6.
4. Дипольное взаимодействие трёх наночастиц
 |
Рассмотрим случай взаимодействия третьей частицы с
агрегированной парой двух других. Все три наночастицы серебра считаются
одинаковыми, и сферическими с радиусом R.
Расстоянием между ними парой первых частиц ![]() ,
расстояние между второй и третьей –
,
расстояние между второй и третьей – ![]() (см. рис. 7.7).
Угол между r12
и r23
обозначим q, а угол между r12
и r13
–
(см. рис. 7.7).
Угол между r12
и r23
обозначим q, а угол между r12
и r13
– ![]() . Поляризация внешнего светового поля
направлена под углом a к прямой, соединяющей
. Поляризация внешнего светового поля
направлена под углом a к прямой, соединяющей
Рис. 7.7. Схема взаимного расположения частиц и поля волны
 |
центры двух первых частиц и параллельной оси х. Для аналитического решения и дальнейшего нахождения энергий взаимодействия система уравнений для 3-х частиц слишком громоздка, поэтому ограничимся численным расчетом энергии взаимодействия трех частиц в поле оптического излучения, для конкретных значений параметров.
5. Энергии взаимодействий трех частиц
Как и в предыдущем случае, примем значения величин
радиуса частицы ![]() нм, внешнего поля
нм, внешнего поля ![]() ед.СГС и температуры
ед.СГС и температуры ![]() К. Зависимость энергии взаимодействия
системы частиц от угла
К. Зависимость энергии взаимодействия
системы частиц от угла ![]() и длины волны излучения
приведена на рисунке 7.9. Как видно из рисунка, при расстоянии между
агрегированной парой и третьей частицей
и длины волны излучения
приведена на рисунке 7.9. Как видно из рисунка, при расстоянии между
агрегированной парой и третьей частицей ![]() нм,
и при угле расположения третьей частицы
нм,
и при угле расположения третьей частицы ![]() ,
в зависимости энергии диполь-дипольного взаимодействия третьей частицы с двумя
другими имеется потенциальная яма при ориентации внешнего поля
,
в зависимости энергии диполь-дипольного взаимодействия третьей частицы с двумя
другими имеется потенциальная яма при ориентации внешнего поля ![]() ° и длине волны в
ИК-диапазоне,
° и длине волны в
ИК-диапазоне, ![]() нм. Последнее очевидно из
физических соображений, поскольку минимум потенциальной энергии взаимодействия
соответствует случаю расположения частиц по прямой, параллельной плоскости
поляризации излучения, а сдвиг дна потенциальной ямы в длинноволновую область
увеличивается по сравнению со случаем двух частиц. При перемещении частицы на
нм. Последнее очевидно из
физических соображений, поскольку минимум потенциальной энергии взаимодействия
соответствует случаю расположения частиц по прямой, параллельной плоскости
поляризации излучения, а сдвиг дна потенциальной ямы в длинноволновую область
увеличивается по сравнению со случаем двух частиц. При перемещении частицы на ![]() °, минимум достигается и
при значении
°, минимум достигается и
при значении ![]() °.
°.
 |
|
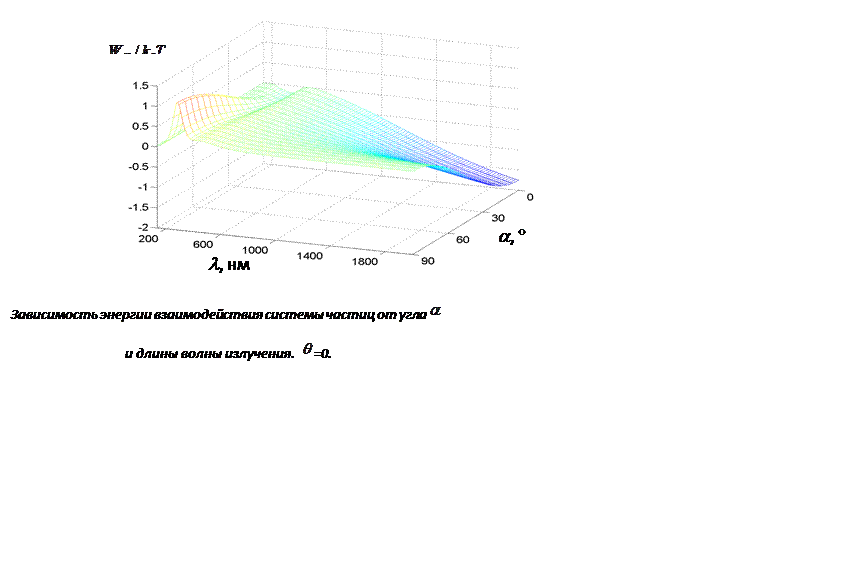
Рис. 7.9. Зависимость энергии взаимодействия системы частиц от угла
![]() и длины волны излучения,
и длины волны излучения, ![]() .
.
При
дальнейшем увеличении угла до ![]() °
(7.10) минимум смещается к
°
(7.10) минимум смещается к ![]() °
и
°
и ![]() нм
нм
|
|
|
|
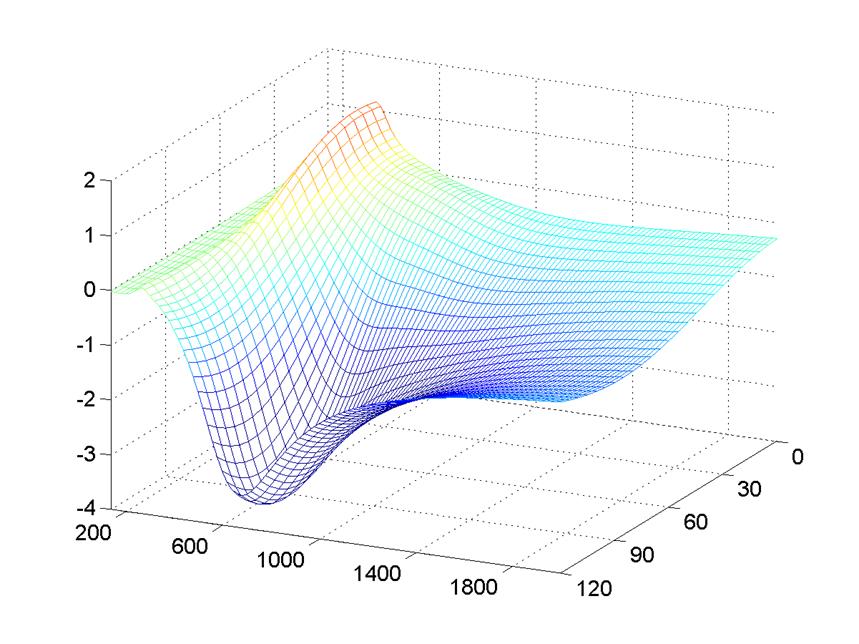
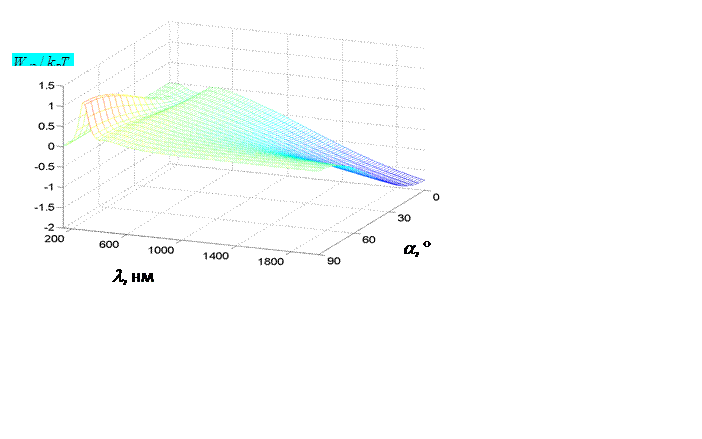
Рис.
7.10. Зависимость энергии взаимодействия системы частиц от угла ![]()
и
длины волны излучения, ![]() .
.
Таким образом, показана возможность самоорганизации наночастиц серебра во внешнем световом поле на примере простейших двух- и трёх-частичных моделей. Самоорганизация происходит за счёт диполь-дипольного взаимодействия частиц, имеющего минимум энергии при определённой конфигурации частиц и соответствующих частоте и поляризации поля. Для контроля агрегирования частиц получены зависимости спектров агрегатов от их геометрии.
Сделанные оценки показывают, что энергия диполь-дипольного взаимодействия может быть соизмерима с энергией взаимодействия Ван-дер-Ваальса и теплового движения частиц.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.