Контроль в технологических процессах обработки информации, страница 3

Поскольку  и ,  то при N>18 количество ненулевых корней оказывается равным нулю, т.е. в этом случае обнаруживаются все сдвиговые ошибки на один разряд.

Для сравнения рассмотрим уравнение сдвига при , которое имеет следующий вид .

При N=37 имеется корень  (), а минимальное значение N, обеспечивающее полное отсутствие корней, равно 73.

В целом  можно сделать вывод, чем больше значение  отличаются от 1 и чем больше значения m и l, тем в большей степени рассеиваются корни соответствующих уравнений сдвига. Максимальное рассеивание происходит при   В этом случае минимальное значение N, обеспечивающее обнаружение всех сдвиговых ошибок определяется неравенством

N > 9ml

¨Прочие случайные ошибки.

В этот класс ошибок входят все остальные ошибки, кроме рассмотренных выше. Основной тип конкретных ошибок составляют многократные независимые. Относительное количество не обнаруживаемых независимых ошибок в пределе стремится к отношению количества разрешенных значений реквизита к общему количеству возможных комбинаций, представленных с учетом внесенной за счет контрольных разрядов избыточности. Следовательно, при контроле по модулю N  количество необнаруженных независимых ошибок стремится к величине 1/N, а процент контролируемых ошибок равен  (N-1)/N. Очевидно, что с точки зрения эффективности контроля случайных ошибок желательно использовать возможно большее значение N. Таким образом, общие требования к выбору значений N и W_i, обеспечивающие эффективность метода по отношению к рассмотренным ошибкам заключается в следующем:

-  значение модуля N должно быть возможно большим простым числом;

-  сумма значений любой группы последовательных смежных весов не должна быть кратна N;

-  разность весов не должна быть равна нулю и не должна быть кратна N.

3.2.2. Основные методы контроля по модулю.

¨Метод Беркли 11(1,2,5,3,6,4,8,7,10,9). В основе метода лежит классическая схема контроля по модулю, в которой N=11.

Контрольные разряды вычисляются

                                           

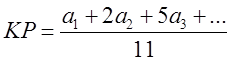
Например: кодовое обозначение 21358432

                                                        78463521

                  

 

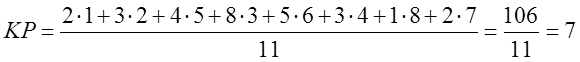
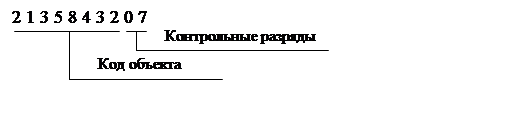Последовательность весов, предложенная Беркли, построена таким образом, в пределах 10-разрядного числа все весы различны, сумма любых групп (пар, троек и т.д.) смежных весов не равна 11, любая группа смежных весов не образует ни арифметической, ни геометрической прогрессии.  Выбранные весы обеспечивают высокую контролирующую особенность метода по отношению к перечисленным выше орфографическим ошибкам.

При использовании данного метода обнаруживают:

-  100% однократных транскрипционных ошибок;

-  100% многократных смежных транскрипционных ошибок;

-  91% случайных ошибок (N-1) = 10/11 = 0,91.

В целом метод обладает достаточно большой контролирующей способностью. Однако поскольку в 9% случаев остаток равен 10, то он должен проставляться либо алфавитным разрядом, либо двумя цифровыми, что не очень удобно. Это является существенным недостатком метода контроля по модулю 11.

Возможные способы сокращения избыточности до одного контрольного разряда заключается в следующем:

1.  Использование дополнительного набора весов для случаев равенства остатка 10.

2.  Простое усечение остатка, т.е. замена 10 на нулевое значение.

3.  Исключение из употребления кодовых комбинаций , дающих остаток 10.

В первых двух случаях получают неэффективные результаты, так как не обнаруживают даже все однократные транскрипционные ошибки, удельный вес которых значителен (около 75%).

Третий способ возможен лишь в тех случаях, когда классификаторы формируются заново, а не совершенствуются добавлением контрольных разрядов.

¨ Методы 11(W_B). Так обозначаются методы контроля по модулю 11 с набором весов, предложенных Бриггстом, который представляется (1,2,4,3,6,10,9,7,8,5). Такой набор позволяет обнаруживать смежные транскрипционные ошибки любой кратности.

Набор весов Беркли разработан, чтобы избежать арифметических и геометрических прогрессий, что в целом излишне и не позволяет выявлять многократные смежные  и раздельные транскрипционные ошибки. Набор весов Бриггста эффективнее набора весов Беркли.

¨ Методы 10[11(W_А)]. Под этим названием объединена группа методов, отличающаяся только набором весов. Сущность метода, предложенного Эндрью, для повышения эффективности контроля цифровых данных состоит в том, что контрольные разряды

                               

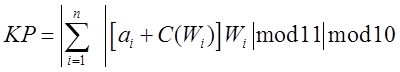
где С(W_i) для данного значения W_i есть такая константа, что  для любых  а = 0,1, …, 9. Этот метод использует один контрольный разряд и позволяет обнаруживать однократные транскрипционные ошибки и значительную часть  двукратных транскрипционных и  транспозиционных ошибок. Предложено несколько равнозначных наборов W_i,  подобранных таким образом, чтобы минимизировать количество необнаруживаемых смежных двукратных транскрипционных и транспозиционных ошибок.

Например (4,5,2,3,10,7,6,9,8,1).

¨ Метод 11(1,10). В данном методе значения контрольных разрядов образуется как остаток от деления исходного числа на 11. Очевидно, это соответствует общей схеме контроля по модулю с весами 1,10,100 … . Поскольку при суммировании значений а_iw_i слагаемые, кратные 11 не участвуют в образовании остатка, естественные десятичные позиционные веса эквивалентны следующей последовательности фактических весов 1,10,1,10. Действительно

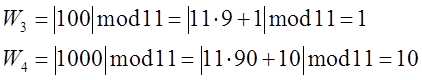                            и т.д.

то есть последовательность весов очень неудачна, веса повторяются с шагом 2 и сумма любой пары смежных весов кратна модулю. Поэтому контролирующая способность метода низка, однако процедура проверки весьма проста.