Для оценки сложности функций (СлФ) устанавливается число трансформаций (Nтранс) - совокупность шагов процесса обработки данных (то есть число операций, преобразующих вход в выход) и семантических утверждений, управляющих выполнением операций. Каждая трансформация «взвешивается» по трем уровням сложности («низкая», «средняя» и «высокая»), подобно тому, как это делалось в FP-методе.
Для оценки сложности управления (СлУ) определяется множество уникальных состояний (Nc), в которых может находиться процесс, а также множество переходов (Nп) между состояниями. Для состояний и переходов устанавливается только один уровень сложности - 1. Сложность управления определяется по формуле:
СлУ = Nc + Nп
Общий функциональный размер приложения вычисляется по формуле: 3D_FP = СлД + СлФ + СлУ
7.2.4. Метод Object Points for ICASE
Метод ObjectPointsforICASE (I_FP), разработанный Д. Бенкером в 1994 году, не обязательно связывать с традиционным объектно-ориентированным подходом. Под объектами здесь понимаются экранные формы (или экраны), формы отчетов (или отчеты) и модули (компоненты языка 3-го поколения). Это стандартные элементы приложений при разработке средствами интегрированных CASE-инструментов.
Расчет функционального размера производится следующим образом [6].
Определяется число объектов каждого вида.
Далее для каждого из этих объектов устанавливается уровень сложности (как «простой», «средний» и «сложный») в зависимости от значений характеристик, представленных в таблице 7.24.
Затем определяются относительные веса элементов в зависимости от уровня сложности (таблица 7.25)
И, наконец, функциональный размер приложения вычисляется как сумма полученных значений по всем объектам.
|
|
|
|
7.2.5. Метод EarlyFunctionPoints. Раннее прогнозирование размера
Метод раннего прогнозирования функционального размера (EFP, от Early Function Points) предложен Роберто Мели (Италия) в 1997 году. FFP - это не альтернатива базовому FP-методу (IFPUG 4.0), а его адаптация для быстрого и раннего оценивания размера.
Метод основывается на идентификации объектов будущего приложения - логических данных и функциональности - на различных уровнях их детализации. Степень неопределенности оценки, представляемой диапазоном «минимум-максимум», тем выше, чем выше уровень, на котором останавливается процесс идентификации объектов приложения. Однако многоуровневый подход делает возможным использование любых знаний (в любой форме и любой глубины), оставляя на время некоторые вопросы о деталях без ответа, и наоборот, не используя существующей детальной информации о части системы.
Ключевыми объектами оценивания являются: функциональные примитивы, микрофункции, функции, макрофункции и логические элементы данных. Каждому из этих объектов может быть назначено множество значений УЕФ, основанных на статистических данных.
Логические элементы данных (ЛЭД) - группы связанных элементов данных, соответствующих ВЛО и ВИО в базовом FP-методе. Они классифицируются по пяти уровням сложности: «низкий», «средний», «высокий», «сложный», «сверхсложный». Первые три оценки выводятся по правилам FP-метода, вторые две -предназначены для оценивания крупных (составных) объектов данных без их детализации (например, объектов, состоящих из нескольких взаимосвязанных таблиц). На стадии раннего прогнозирования размера различия между ВЛО и ВИО не делаются. Матрица оценки сложности составных объектов представлена в таблице 7.26.

Четыре основные категории объектов-функций, характеризующих функциональность приложения таковы:
• функциональные
примитивы (ФПр) - мельчайшие элементарные процес
сы,
которые не могут быть далее детализированы. Это процессы ввода (ПрВВД),
вывода
(ПрВЫВ) и запроса (ПрЗАП), соответствующие объектам ВВД, ВЫВ и ЗАП
в базовом FP-методе;
• микрофункцш (МиФ) - набор из четырех
функциональных примитивов -
создание,
выборка, обновление и удаление, выполняемых над элементарными дан
ными
одного или нескольких объектов данных. То есть, это функции управления
(ведения)
данных;
• функции (Фун) - набор функциональных
примитивов средней сложности,
которые
могут быть ассоциированы с операционными потребностями пользовате
лей
приложения. Матрица оценки их сложности представлена в таблице 7.27;

|
|
|
Все объекты EFP-метода далее связываются с тремя весовыми категориями -«минимум», «среднее» и «максимум» (таблица 7.29). |
• макрофункиии (МаФ) - набор функций средней сложности. Их можно ассоциировать с фрагментом приложения, с целым приложением или со всей системой потребителя. Матрица оценки их сложности представлена в таблице 7.28.
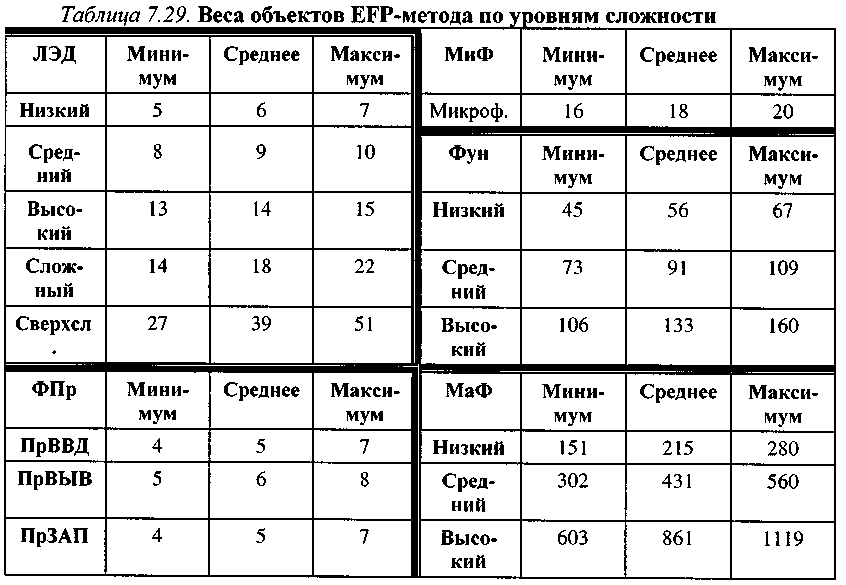
Эти значения весов могут корректироваться по мере сбора и обработки данных в реальных проектах.
Для определения прогнозируемого размера приложения в УЕФ необходимо определить количество объектов всех видов по каждому уровню сложности и полученные значения просуммировать.
Не существует достаточно четкого описания метода идентификации объектов - можно «отталкиваться» как от объектов-данных, так и от объектов-функций (деловых процессов пользователя). Многое зависит от знания и опыта экспертов, выполняющих анализ предметной области, в которой будет работать система. Некоторые рекомендации можно найти в работе Л. Сантилло и Р. Мели [7].
7.2.6. Метод FullFunctionPointsи его разновидности
Метод FullFunctionPoints (FFP) - наиболее интересное развитие методологии FPA. Он предложен в 1997 А. Эбреном из UQAM (университет в Квебеке, Монреаль, Канада) и поддерживается Международным Консорциумом COSMIC (Common Software Measurement International Consortium) [8].
Метод в большей степени ориентирован на системы реального времени (в том числе системы телекоммуникации, системы управления процессами) и встроенные системы (системы управления устройствами), но может использоваться и в универсальном контексте (системы организационного управления, включая банковские, бухгалтерские и др., обеспечивающие обработку больших объемов данных). Однако он не предназначен для определения размера компонентов ПО, имеющих большую математическую сложность или поддерживающих аудио- и видео-образы (компьютерные игры, программы музыкальных инструментов и др.).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.