Построение диаграммы рассеяния. Одновыборочный критерий Колмогорова-Смирнова, страница 2

a  Поправка значимости Лильефорса

По критериям Колмагорова-Смирнова и Шапиро-Уилка значимость равна 0,000, что меньше значения 0,05, поэтому распределение не является нормальным. Также это можно увидеть на графиках.

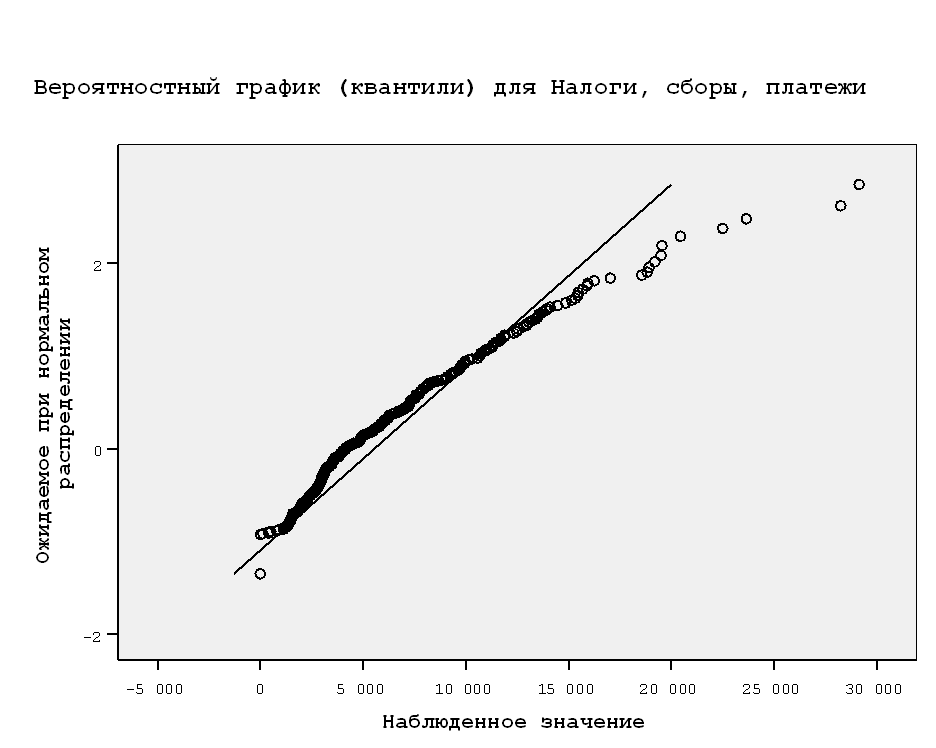
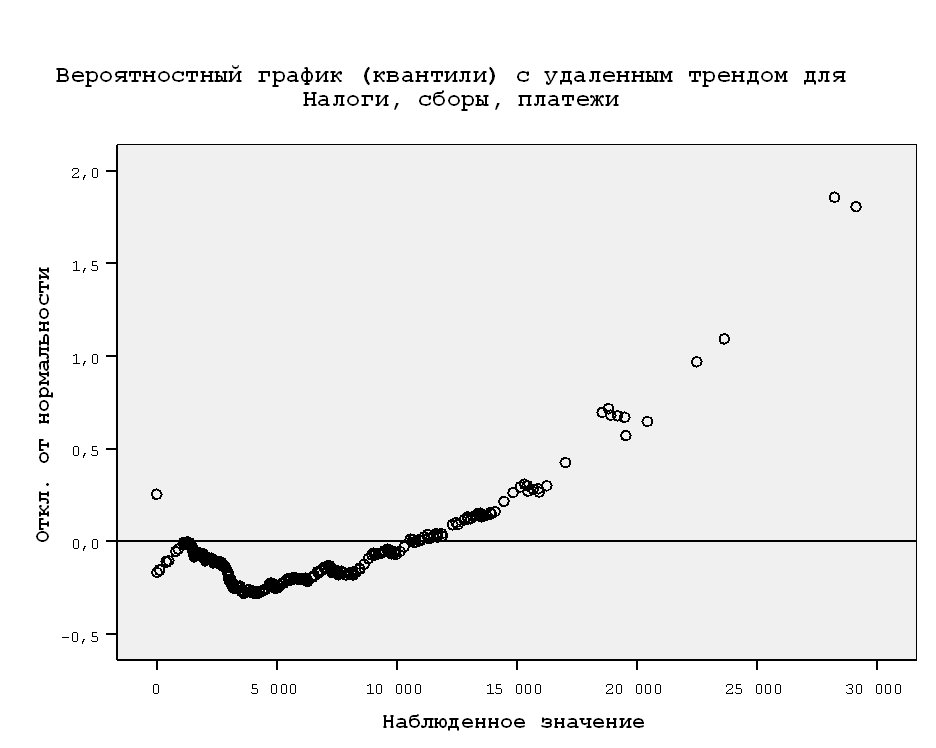
5.  Приводим к нормальности путем преобразований.

1)  Преобразование переменной: доля налогов в расходах на конечное потребление.

Преобразовать -> Вычислить

Создала переменную Dolya = nalog / rassq

Теперь проверяем на нормальность всеми тремя способами переменную Dolya

Гипотеза H₀: y є N

1.1)  Анализ -> Описательные статистики-> Описательные (Параметры… )

Выбираем Dolya.

                                                                                                      Описательные статистики

 

	N	Минимум	Максимум	Среднее	Стд. отклонение	Асимметрия		Эксцесс
	Статистика	Статистика	Статистика	Статистика	Статистика	Статистика	Стд. ошибка	Статистика	Стд. ошибка
Dolya	456	,00	,60	,0974	,07670	1,362	,114	5,210	,228
N валидных (целиком)	456

Проверяем условия: |А|≤3*S_A; |Э|≤5*S_Э

1,362 ≤ 3*0,114; 5,210 ≤ 5*0,228

Оба условия не выполняются, поэтому гипотеза о нормальности распределения отвергается.

1.2)  С помощью критерия Колмагорова-Смирнова

Анализ -> Непараметрические критерии (не взвешивать)

Условие: p < 0,05 – не нормальное распределение (p – Ассимпт.знч. (двустороннее))

              Одновыборочный критерий Колмогорова-Смирнова

 

 

 

		Dolya
N		456
Нормальные параметры(a,b)	Среднее	,0974
	Стд. отклонение	,07670
Разности экстремумов	Модуль	,102
	Положительные	,075
	Отрицательные	-,102
Статистика Z Колмогорова-Смирнова		2,177
Асимпт. знч. (двухсторонняя)		,000

a  Сравнение с нормальным распределением.

b  Оценивается по данным.

0,000<0,05 следовательно распределение не нормальное

1.3)  Анализ -> Описательные статистики -> Исследовать

Графики…

Графики критерии для проверки нормальности

                                                            Критерий нормальности

 

	Колмогоров-Смирнов(a)			Шапиро-Уилк
	Статистика	ст. св.	Значимость	Статистика	ст. св.	Значимость
Dolya	,102	456	,000	,904	456	,000

a  Поправка значимости Лильефорса

По критериям Колмагорова-Смирнова и Шапиро-Уилка значимость равна 0,000, что меньше значения 0,05, поэтому распределение не является нормальным. Также это можно увидеть на графиках.

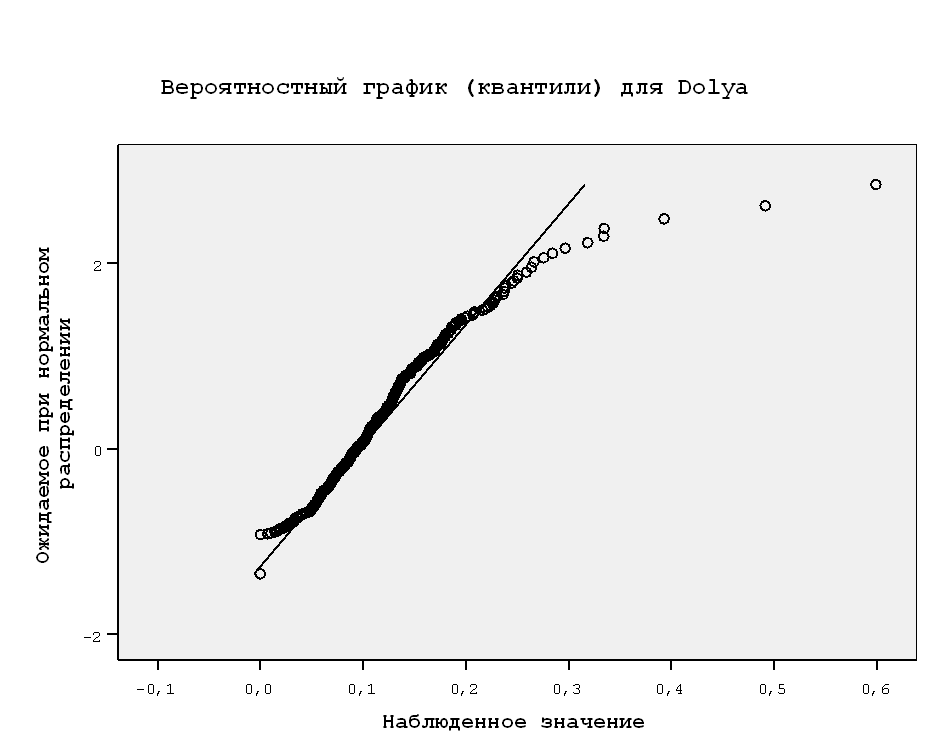
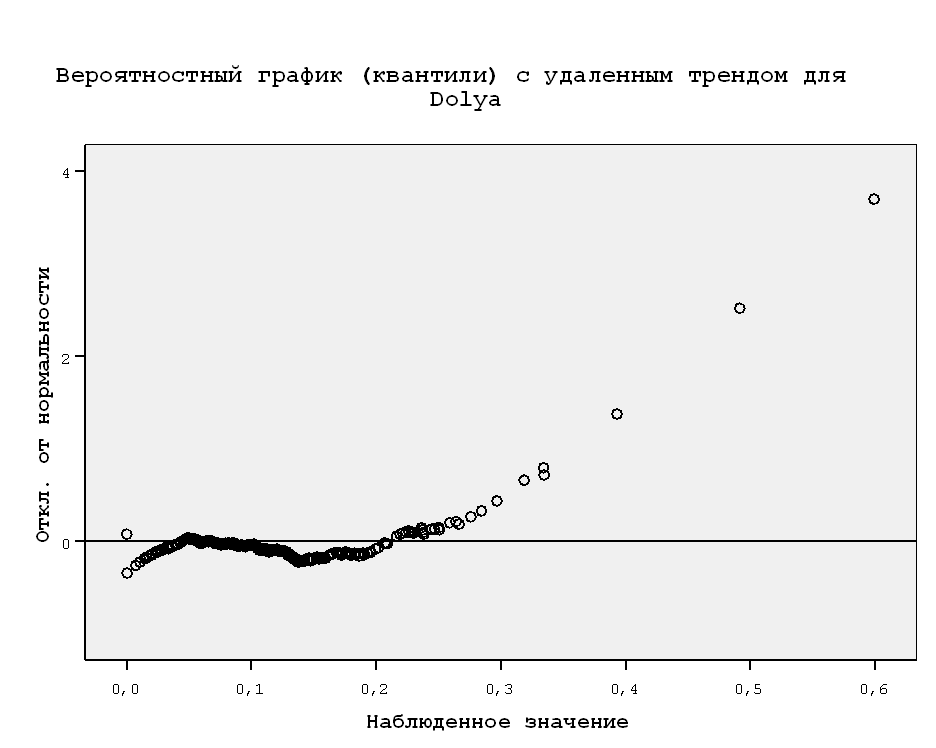
2)  Приводим к нормальности, поделив y на количество взрослых членов

Преобразовать -> Расчет

Создала переменная VzChl= nalog / (chlicn-chdet)

Теперь проверяем на нормальность всеми тремя способами переменную VzChl

Гипотеза H₀: y є N

1.1)  Анализ -> Описательные статистики-> Описательные (Параметры… )

Выбираем VzChl.

                                                                                                  Descriptive Statistics

	N	Minimum	Maximum	Mean	Std. Deviation	Skewness		Kurtosis
	Statistic	Statistic	Statistic	Statistic	Statistic	Statistic	Std. Error	Statistic	Std. Error
VzChl	456	,00	16251,52	2739,2416	2454,06811	1,575	,114	4,208	,228
Valid N (listwise)	456

Проверяем условия: |А|≤3*S_A; |Э|≤5*S_Э         

1,575 ≤ 3*0,114; 4,208 ≤ 5*0,228

Оба условия не выполняются, поэтому гипотеза о нормальности распределения отвергается.

1.2)  С помощью критерия Колмагорова-Смирнова

Анализ -> Непараметрические критерии (не взвешивать)

Условие: p < 0,05 – не нормальное распределение (p – Ассимпт.знч. (двустороннее))

                       One-Sample Kolmogorov-Smirnov Test

 

 

 

		VzChl
N		456
Normal Parameters(a,b)	Mean	2739,2416
	Std. Deviation	2454,06811
Most Extreme Differences	Absolute	,132
	Positive	,095
	Negative	-,132
Kolmogorov-Smirnov Z		2,822
Asymp. Sig. (2-tailed)		,000

a  Test distribution is Normal.

b  Calculated from data.

0,000<0,05 следовательно распределение не нормальное

1.3)  Анализ -> Описательные статистики -> Исследовать

Графики…

Графики критерии для проверки нормальности

                                                           Tests of Normality

 

	Kolmogorov-Smirnov(a)			Shapiro-Wilk
	Statistic	df	Sig.	Statistic	df	Sig.
VzChl	,132	456	,000	,876	456	,000

a  Lilliefors Significance Correction

По критериям Колмагорова-Смирнова и Шапиро-Уилка значимость равна 0,000, что меньше значения 0,05, поэтому распределение не является нормальным. Также это можно увидеть на графиках.

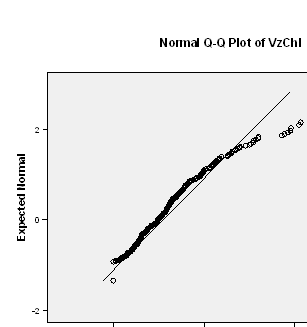
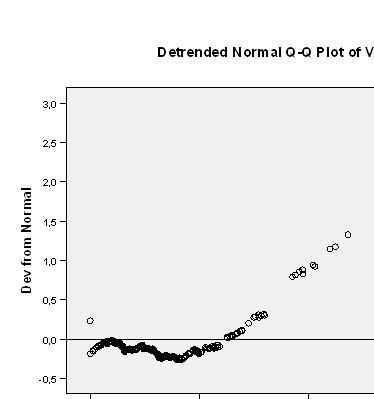
3)  Приводим к нормальности, вычислив логарифм

Преобразовать -> Расчет

Создала переменная LnY= LN(nalog)

Теперь проверяем на нормальность всеми тремя способами переменную LnY

Гипотеза H₀: y є N

1.1)  Анализ -> Описательные статистики-> Описательные (Параметры… )

Выбираем LnY.