Экономика и менеджмент \ Математическая экономика

Классификация векторных задач математического программирования. Однородные и неоднородные ВЗМП. ВЗМП с равнозначными критериями, страница 2

ВЗМП 1 при равнозначных критериях решена, если найдена точка  и такая верхняя оценка , что

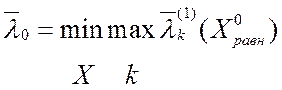                                                                                   (2.4.7)

Т.е., и здесь ВЗМП 1 может быть сведена здесь к соответствующей скалярной задаче:

                                                                      (2.4.8)

Соответственно, задача (2.4.8) называется  - задачей и ее решение методом ГРНК дает единственную точку , которая оптимальна по Парето.

Точно так же строятся принципы оптимальности для решения ВЗМП 2, только формулировки, как уже говорилось, будут “противоположными”.

ВЗМП 2 при равнозначных критериях решена, если найдена точка  и такой верхний уровень  или нижняя оценка , что:

              или        .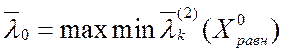         

Таким образом, ВЗМП 2 так же сводится к скалярной задаче:

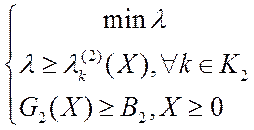                  или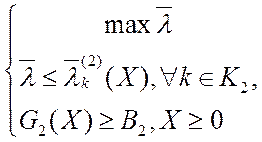                

ВЗМП 3 при равнозначных критериях решена, если найдена точка  и такой нижний уровень  или верхняя оценка , что:

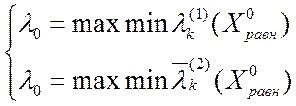или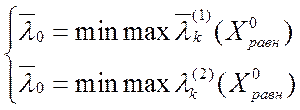        

таким образом, ВЗМП 3  сводится к скалярной задаче:

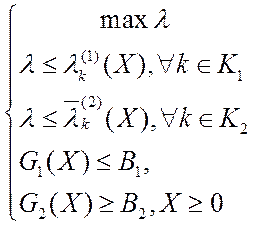                  или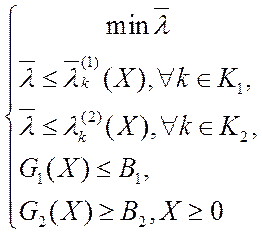                

2.4.4.  Алгоритм решения ВЗМП с равнозначными критериями.

Шаг 1.

Найти оптимумы для каждого критерия.

·  Для ВЗМП 1:

Решить l1 – (по числу критериев) – скалярных задач оптимизации:

                                                            

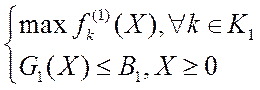
а также, соответственно, l1 скалярных задач:

                                                             

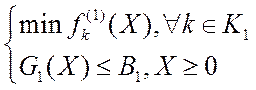
чтобы получить значения и ,.

·  Для ВЗМП 2:

Решить 2l2 – (по числу критериев) – скалярных задач оптимизаци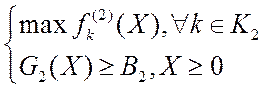и:

                       и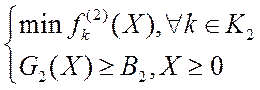         

·  Для ВЗМП 3:

Решить 2(l1+l2) скалярных задач:

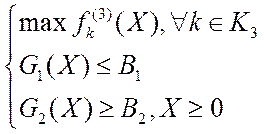                        и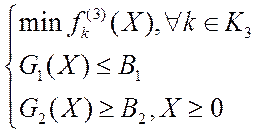               

Шаг 2.

Выполнить единую нормализацию критериев.

·  Для всех ВЗМП одинаково:

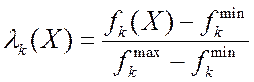                      или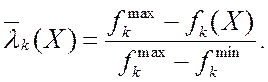         

Шаг 3.

Построить  -  или  - задачу.

·  Для ВЗМП 1:

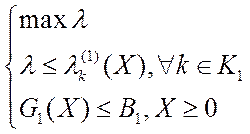                       или          

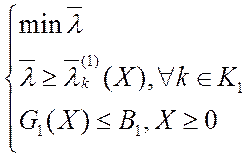
·  Для ВЗМП 2:

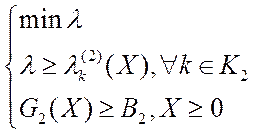                       или       

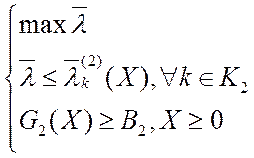
·  Для ВЗМП 3:

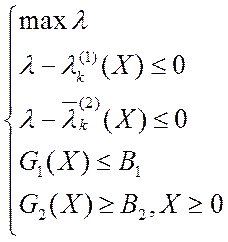                          или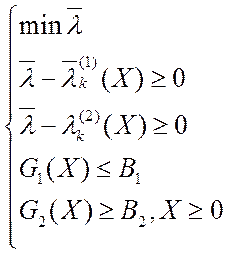       

Шаг 4.

Решаем   -  или  - задачу и находим единственную точку , оптимальную по Парето, в которой гарантируем результат:

·   Для ВЗМП 1:

                       или 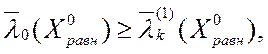                (2.4.9)

·  Для ВЗМП 2:

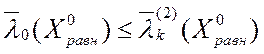                           или       ,        (2.4.10)          

·  Для ВЗМП 3:

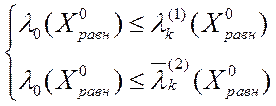                    или 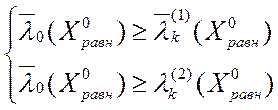     .                                                              (2.4.11)

Шаг 5.

Зная величину нормализованного критерия в точке , по формулам (2.4.1) и (2.4.2) легко находим необходимые значения каждого критерия

2.5.  ВЗМП с неравнозначными критериями.

Здесь, точно так же, как и в п.2.4. необходимо сначала нормализовать критерии, а потом определить для них принципы оптимальности. Но в плане нормализации, очевидно, все будет абсолютно идентично ВЗМП с равнозначными критериями, поэтому считаем, что критерии неравнозначной ВЗМП (2.3.9) приведены к единому нормализованному виду (2.4.1) или (2.4.2).

2.5.1.  Определение приоритета критериев.

Как уже говорилось, частные критерии в ВЗМП имеют на практике разный вес – разную важность. Идея определения приоритета критериев состоит в том, чтобы ЛПР:

1)  мог бы заданием большего веса улучшить значение определенного, важного для него критерия;

2)  мог задать этот вес не интуитивно, а на достаточно строгой математической, т.е. объективной основе.

Пусть, например, нам важен критерий с индексом q и его относительный уровень в ВЗМП 1 - . Чтобы улучшить его, необходимо найти такую точку , в которой . Но, очевидно, что увеличивая относительный уровень q – критерия, мы будем изменять уровни других критериев, т.к. все они связаны по ,поэтому, чтобы улучшать уровень q – критерия целенаправленно, необходимо установить связь между q – критерием и всеми остальными.

В ВЗМП 1 связь q – критерия со всеми остальными критериями определяется вектором

,

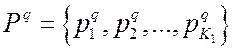где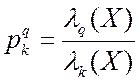- коэффициент связи частных критериев q и k, .

Если в ВЗМП 1, в т. имеем , то говорят, что q – критерий имеет приоритет по отношению к k – критерию.

Если в ВЗМП 2, в т. имеем , то говорят, что q – критерий имеет приоритет по отношению к k – критерию.

Если в ВЗМП 3, в т. имеем , то говорят, что q – критерий имеет приоритет по отношению к k – критерию.

В ВЗМП 1 и ВЗМП 3 множество точек  называется областью приоритета q–критерия над всеми другими, если .

Точно такая же область в ВЗМП 2 определяется условиями ,

.

2.5.2. Принципы оптимальности решения неравнозначных ВЗМП.

Для их построения воспользуемся принципом гарантированного результата и зададим в ВЗМП 1 нижний уровень q – критерия, который необходимо достичь ЛПР, исходя из требований практики.

Очевидно, этот уровень будет определяться выражением

или, соответственно,

          .

Таким образом, выбором некоторого значения  мы можем определить нижний уровень q – критерия

                                               .

Тогда, увеличивая его (), мы сможем улучшить значение q –критерия и, с помощью коэффициентов связи, проследить за изменениями остальных критериев.

ВЗМП 1 с неравнозначными критериями считается решенной относительно q – критерия, если найдена точка  и нижний уровень  такой, что:

                                        ,                                                                  (2.5.1)

. Стало быть, решение ВЗМП 1 опять сводится к решению скалярной задачи:

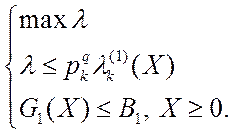                                                                                                                (2.5.2)

ВЗМП 2 с неравнозначными критериями считается решенной относительно q – критерия, если найдена точка  и верхний уровень  такой, что:

                                        ,                                                                  (2.5.3)

, а для этого необходимо решить скалярную задачу:

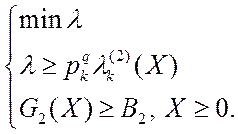                                                                                                                (2.5.4)

ВЗМП 3 с неравнозначными критериями считается решенной относительно q – критерия, если найдена точка  и нижний уровень  такой, что:

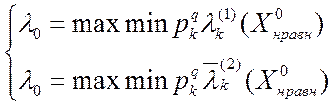                                      ,                                                                  (2.5.5)

, и найти решение скалярной задачи:

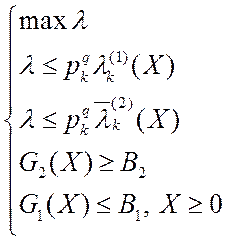                                                                                                                 (2.5.6)

При этом точки , полученные при решении каждой ВЗМП, будут единственными и оптимальными по Парето. Задачи (2.5.1) – (2.5.3) являются  - задачами для решения соответствующей ВЗМП. Совершенно аналогично можно построить принципы оптимальности, используя относительные отклонения .

Остается определить, как найти значение, чтобы решить  - задачу, а с ней и ВЗМП с неравнозначными критериями. Для этого ЛПР необходимо выбрать любое число из диапазона:

                     ,,

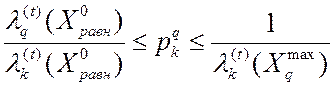где  - точка компромиссного решения соответствующей ВЗМП с равнозначными критериями, а  - точка, в которой q – критерий достигает своего максимума при решении «своей» скалярной задачи. В общем случае, диапазон чисел

            ,

представляет собой «траекторию движения» от точки , где критерии равнозначны, до точки , где q – критерий имеет наибольший приоритет над остальными.

2.5.3.  Алгоритм решения ВЗМП с неравнозначными критериями.

Для любой ВЗМП  количество принципиальных шагов алгоритма будет одинаковым. Разница будет в числе операций на первом шаге.

Шаг 1.

Решаем соответствующую ВЗМП с равнозначными критериями (см.п.2.4.4.). Находим точку , где достигается ,  и точку , где достигается гарантированный результат (2.4.9) – (2.4.11).

Шаг 2.

ЛПР проводит анализ результатов решения и, по величине , определяет q – критерий, значения которого необходимо улучшить.

Шаг 3.

Определяются пределы изменения коэффициентов связи выбранного q – критерия по отношению к остальным:

                                        ,

где 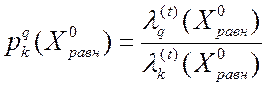, а  ; .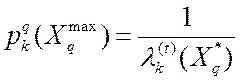

Шаг 4.

ЛПР выбирает необходимую величину  и строит  - задачу  (2.5.2),  (2.5.4) или (2.5.6), решая которую находит точку компромиссного решения

, где достигается гарантированный результат (2.5.1), (2.5.3) или (2.5.5).

Шаг 5.

Зная величину нормализованных критериев в точке , по формулам (2.4.1) и (2.4.2), легко находим компромиссные значения каждого критерия .

ЛИТЕРАТУРА

[1] Хоменюк В.В. Элементы теории многоцелевой оптимизации. – М.: Наука, 1983. – 124с.

[2] Машунин Ю.К. Методы и модели векторной оптимизации. – М.: Наука. 1986. – 140с.

[3] Карпелевич Ф.И., Садовский Л.Е. Элементы линейной алгебры и линейного программирования. – М.: Наука, 1965. – 276с.

Скачать файл