2.2. Классификация векторных задач математического программирования (ВЗМП)
Любую из многочисленных ВЗМП, поставленных и исследованных в настоящее время, можно свести к одному из следующих типов, в соответствии с выбранными признаками-классификаторами.
1. По характеру оптимизации каждого критерия:
а) однородные ВЗМП – в которых все критерии оптимизируются одинаково (либо max, либо min);
б) неоднородные ВЗМП – где часть критериев максимизируется, для остальных ищется минимум.
2. По характеру предпочтений ЛПР:
а) равнозначные ВЗМП – в которых ЛПР не отдает предпочтений ни одному из критериев, считая их все равноценными;
б) неравнозначные ВЗМП – где ЛПР определяет приоритет каждого критерия, ранжируя их по важности.
3. По виду
целевых функций ![]() и ограничений
и ограничений ![]() :
:
а) линейные
ВЗПМ – все ![]() и
и ![]() линейны
относительно
линейны
относительно ![]() ;
;
б) нелинейные
ВЗМП – хотя бы одна из ![]() или
или ![]() является нелинейной.
является нелинейной.
4. По типу
переменных ![]() :
:
а) непрерывные
ВЗМП – все ![]() могут принимать любые
неотрицательные, действительные значения;
могут принимать любые
неотрицательные, действительные значения;
б) дискретные
ВЗМП – все (или частично) ![]() могут быть любыми
из некоторого дискретного множества, в частности, целых чисел;
могут быть любыми
из некоторого дискретного множества, в частности, целых чисел;
в) стохастические
ВЗМП – в которых все (или частично) ![]() принимают
некоторые значения лишь с определенной вероятностью.
принимают
некоторые значения лишь с определенной вероятностью.
Первые 2 признака являются основными, т.к. они определяют принципы построения алгоритма решения. Остальные – вспомогательные, поскольку принципиально не влияют на характер алгоритма, а лишь определяют его модификации.
Рассмотрим теперь принципы, на которых должна основываться методика решения различных типов ВЗМП. Для этого, сначала, сделаем постановку ВЗМП в соответствии с классификацией, предложенной выше.
2.3. Однородные и неоднородные ВЗМП
2.3.1. Однородные ВЗМП.
Определим однородную ВЗМП с максимизацией критериев (назовем ее ВЗМП 1) в следующей постановке. Найти:
![]() ,
,
если
![]()
![]() ,
,
где 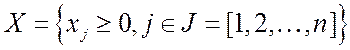 - вектор неизвестных;
- вектор неизвестных;
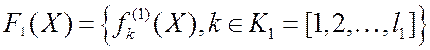 - вектор
критериев;
- вектор
критериев;
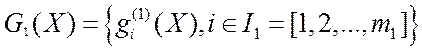 - вектор ограничений;
- вектор ограничений;
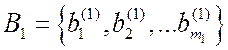 - вектор, определяющий уровень
ограничений.
- вектор, определяющий уровень
ограничений.
Пусть
также ![]() - вогнутые,
- вогнутые, ![]() -
выпуклые функции, а область допустимых решений ВЗМП 1 не является пустым
множеством:
-
выпуклые функции, а область допустимых решений ВЗМП 1 не является пустым
множеством:
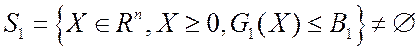 .
.
Рассмотрим также однородную ВЗМП с минимизацией критериев (назовем ее ВЗМП 2) в следующей постановке. Найти:
![]() ,
,
если
![]()
![]() ,
,
где 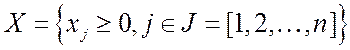 - вектор неизвестных;
- вектор неизвестных;
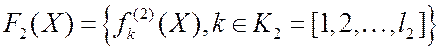 - вектор
критериев;
- вектор
критериев;
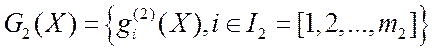 - вектор ограничений;
- вектор ограничений;
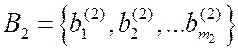 - вектор, определяющий уровень
ограничений.
- вектор, определяющий уровень
ограничений.
Пусть
также ![]() - вогнутые,
- вогнутые, ![]() -
выпуклые функции, а область допустимых решений ВЗЛП 2 не является пустым множеством:
-
выпуклые функции, а область допустимых решений ВЗЛП 2 не является пустым множеством:
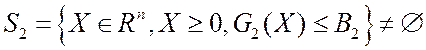 .
.
2.3.2. Неоднородные ВЗМП.
Теперь определим неоднородную ВЗМП (назовем ее ВЗМП 3). Требуется найти:
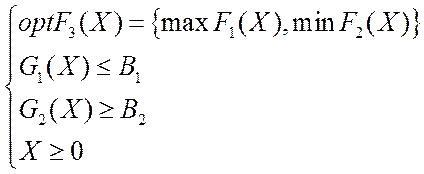
где 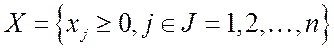 - вектор неизвестных;
- вектор неизвестных;
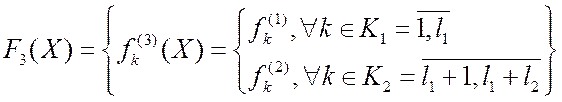 ;
;
![]() - множество
индексов критериев ВЗМП 3;
- множество
индексов критериев ВЗМП 3;
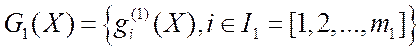 -
вектор ограничений;
-
вектор ограничений;
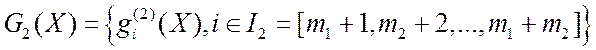 -
вектор ограничений;
-
вектор ограничений;
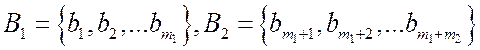 - заданные уровни ограничений.
- заданные уровни ограничений.
Пусть функции ![]() -вогнутые;
-вогнутые;
![]() -выпуклые,
а область допустимых решений ВЗМП 3 не является пустым множеством:
-выпуклые,
а область допустимых решений ВЗМП 3 не является пустым множеством:
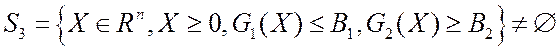
2.4. ВЗМП с равнозначными критериями.
В соответствии с замечаниями, изложенными в п.2.1.4. необходимо, в первую очередь, установить принципы (аксиомы) равенства критериев ВЗМП, а для этого, очевидно, их следует нормализовать. Только в том случае, когда все разнородные критерии будут приведены к одинаковому, безразмерному виду их можно обоснованно сравнивать между собой.
2.4.1. Нормализация критериев в равнозначных ВЗМП.
Для нормализации критериев в ВЗМП общем случае используется линейное преобразование вида:
![]() ,
,![]() ,
,
или
![]() ,
,
где ![]() - исходное значение критерия;
- исходное значение критерия; ![]() - нормализованное значение; a и c – некоторые
константы.
- нормализованное значение; a и c – некоторые
константы.
Такая
нормализация в ВЗМП не влияет на результат решения. Действительно, если ![]() ,
, ![]() , то в точке оптимума
, то в точке оптимума ![]() имеем
имеем 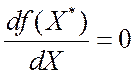 . Тогда и
. Тогда и 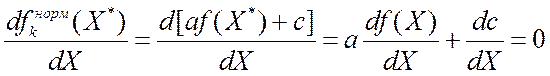 ,
т.е. результат идентичен.
,
т.е. результат идентичен.
В ВЗМП 1 критерии считаются нормализованными, если:
1)
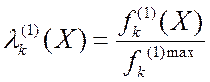 , если
, если ![]() , где
, где ![]() ,
, ![]() ,
, ![]() , причем
, причем ![]() .
.
2)
Более общий случай: если ![]() , где
, где ![]() ,
тогда
,
тогда
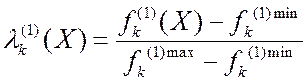 ,
, ![]() ,
, ![]() , и тоже
, и тоже ![]() .
.
Здесь ![]() имеет естественный физический
(экономический) смысл как относительный уровень достижения k-м
критерием своего максимума.
имеет естественный физический
(экономический) смысл как относительный уровень достижения k-м
критерием своего максимума.
Можно вводить
и другую относительную величину – относительное отклонение от достижения k-м критерием своего максимума - ![]() . Тогда нормализация будет иметь вид:
. Тогда нормализация будет иметь вид:
1) 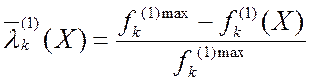 ,
,
![]() ,
, ![]() ,
,![]() ;
;
2)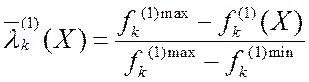 ,
,![]() ,
,![]() ,
,![]() .
.
Совершенно аналогично
нормализуются критерии в ВЗМП 2, как с помощью относительных уровней ![]() , так и с помощью относительных отклонений
, так и с помощью относительных отклонений
![]() .
.
В ВЗМП 3 используется обобщенный нормализованный критерий вида:
1) 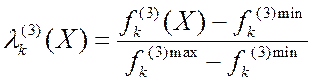 ,
, ![]() ,
, ![]() ; (2.4.1)
; (2.4.1)
или
2) 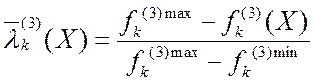 ,
, ![]() ,
, ![]() . (2.4.2)
. (2.4.2)
Совершенно очевидно, что между относительными
уровнями ![]() и относительными
отклонениями
и относительными
отклонениями ![]() существует
однозначная связь:
существует
однозначная связь: ![]() Этим единым
нормализованным критерием мы и будем пользоваться в дальнейшем
Этим единым
нормализованным критерием мы и будем пользоваться в дальнейшем
2.4.2 Принципы равенства критериев ВЗМП.
Идея здесь
проста: сравнивать критерии по величине их ![]() - относительных уровней, или
- относительных уровней, или ![]() - относительных отклонений.
- относительных отклонений.
В любой ВЗМП
два критерия k и q
(![]() ) будут считаться
равными в точке
) будут считаться
равными в точке ![]() , если
, если ![]() ,
, ![]() . Или: два критерия k и q равны в точке
. Или: два критерия k и q равны в точке ![]() , если
, если ![]() ,
, ![]() .
.
Критерии ![]() в ВЗМП считаются равнозначными,
если
в ВЗМП считаются равнозначными,
если ![]() возможна операция
сравнения по числовой величине относительных оценок
возможна операция
сравнения по числовой величине относительных оценок ![]() ,
, ![]() между собой, при этом на каждый
критерий
между собой, при этом на каждый
критерий ![]() и соответственно
и соответственно ![]() не накладывается условий о
приоритетах критериев.
не накладывается условий о
приоритетах критериев.
Некоторая
числовая характеристика всех относительных оценок λ называется
нижним уровнем всех ![]() ,
если
,
если ![]() ,
, ![]() ,
, ![]() , т.е.
, т.е. ![]() . Соответственно, уровень λ
называется верхним для всех относительных уровней
. Соответственно, уровень λ
называется верхним для всех относительных уровней ![]() , если
, если![]() ,
,![]() ,
, ![]() , т.е.
, т.е. ![]() .
.
Аналогично
для отклонений: оценка ![]() называется
верхней среди всех относительных отклонений
называется
верхней среди всех относительных отклонений ![]() , если
, если ![]() ,
, ![]() ,
, ![]() , т.е.
, т.е. ![]() , а оценка
, а оценка ![]() называется нижней для всех
относительных отклонений
называется нижней для всех
относительных отклонений ![]() ,
если
,
если![]() ,
,![]() ,
,![]() , т.е.
, т.е. ![]() .
.
Эти определения мы будем использовать при построении принципов оптимальности решения ВЗМП 1 и 3 с равнозначными критериями. Для ВЗМП 2 они “подойдут” с точностью до наоборот.
2.4.3. Принципы оптимальности решения равнозначных ВЗМП.
Идея
построения этих принципов также несложна: поскольку нижний уровень ![]() является функцией, необходимо найти
его максимум в некоторой точке
является функцией, необходимо найти
его максимум в некоторой точке ![]() , тогда все
критерии
, тогда все
критерии ![]() должны быть в
этой точке не хуже его.
должны быть в
этой точке не хуже его.
ВЗМП 1 при
равнозначных критериях решена, если найдена точка ![]() и
такой нижний уровень
и
такой нижний уровень ![]() ,
что:
,
что:
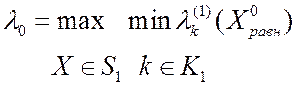 (2.4.3)
(2.4.3)
Таким образом, ВЗМП 1 может быть
сведена к следующей скалярной задаче: найти ![]() такое, что
такое, что
![]() , (2.4.4)
, (2.4.4)
при дополнительных ограничениях:
![]() ,
, ![]() (2.4.5)
(2.4.5)
и основных ограничениях:
![]() и
и ![]() . (2.4.6)
. (2.4.6)
Полученную
задачу (2.4.3) - (2.4.6), называют λ – задачей. Ее решение будем
называть решением ВЗМП, полученным на основе принципа гарантированного
результата и нормализации критериев (в дальнейшем метод ГРНК). Очень важно
отметить, что точка оптимума ![]() , полученная при
решении ВЗМП 1 методом ГРНК, оптимальна по Парето, причем такая точка только
одна. Кроме того, среди решений ВЗМП 1 методом ГРНК всегда найдется два
критерия p и q
, полученная при
решении ВЗМП 1 методом ГРНК, оптимальна по Парето, причем такая точка только
одна. Кроме того, среди решений ВЗМП 1 методом ГРНК всегда найдется два
критерия p и q ![]() , для которых
справедливо равенство:
, для которых
справедливо равенство:
![]() .
.
а остальные критерии удовлетворяют неравенству:
![]() , k
, k ![]() p
p ![]() q,
q, ![]() .
.
Таким образом, величина ![]() и есть гарантированный (не меньше)
результат, откуда, собственно, и происходит название метода.
и есть гарантированный (не меньше)
результат, откуда, собственно, и происходит название метода.
Точно также можно
сформулировать принципы оптимальности решения ВЗМП 1 для относительных отклонений:
необходимо взять максимальное из отклонений ![]() и найти его минимум в некоторой
точке
и найти его минимум в некоторой
точке ![]() , тогда относительное отклонение
любого критерия в этой точке будет не больше его.
, тогда относительное отклонение
любого критерия в этой точке будет не больше его.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.