Тема 9.
Применение морфологического подхода при принятии плановых решений при
позаказной системе производства
9.1. Особенности объемно-календарного планирования при позаказной системе производства
При принятии плановых решений, каких как:
• распределение годовой производственной программы предприятия по плановым периодам (кварталам, месяцам);
• по производственным участкам;
• автоматическим линиям;
• рабочим местам;
• при оперативной проектировке планов;
• перестройке производства и т. д.
необходимо разрабатывать возможные варианты решения и выбирать из них наилучший с точки зрения определения критериев и ограничений.
Моделирование таких задач существенно усложняется при позаказной системе планирования, особенно в условиях разнотипного производства, которое характеризуется рядом особенностей, затрудняющих применение при решении таких задач методов математического программирования.
Особенности:
1. Модели математического программирования не позволяют учесть многие важные производственно-экономические факторы, такие как:
• необходимость выпуска изделий партиями или отдельными заказами, которые нецелесообразно дробить по отдельным плановым периодам;
• целесообразность концентрации изготовления однотипных изделий в одних или смежных плановых периодах;
• непрерывность изготовления изделий с длительностью производственного цикла больше планового периода;
• приоритет отдельных заказчиков в получении продукта.
2. Задачу распределения производственной программы по плановым периодам или производствам не всегда можно или целесообразно сводить к наиболее исследованной задаче линейного программирования из-за нелинейности или дробно-линейного характера зависимостей переменных, большая мерность.
3. При позаказной системе планирования даже однотипного производства возникают трудности при определении переменной модели математического программирования, если учесть упомянутое выше требование отсутствия дробления заказов по плановым периодам или участкам производства (что может случиться при выборе в качестве переменной программирования отдельного изделия); в условиях же однотипного производства, когда изделия существенно отличаются друг от друга трудоемкостью изготовления, объемами реализации и другими показателями, определить переменную модели математического программирования можно только путем введения каких-либо условных, сравнимых заказов или партий, что весьма затрудняет интерпретацию результатов моделирования.
4. В реальной действительности приходится сталкиваться не только со сложностью разработки модели, но и с трудностью установления показателей оптимальности и ограничений, которые в условиях конкретного предприятия имеют наибольшее значение.
Одним из путей преодоления этих трудностей является поиск эвристических процедур и формирование на их основе имитационных моделей, с помощью которых можно учесть многие из рассмотренных выше факторов. Однако такой подход связан со значительными затратами времени и требует достаточно высокой квалификации и опыта плановых работников.
Поиск подхода к моделированию подобных задач заставил обратиться к системному анализу, который занимает промежуточное положение между формальными и эвристическими моделями. Идут по пути разработки человеко-машинных процедур принятия решений, которые позволяют учитывать бóльшее число реальных факторов производства, чем формальные модели.
В частности, одна из таких процедур была разработана на основе метода морфологического ящика.
Приведем вначале упрощённый пример.
9.2. Морфологическое моделирование задач планирования при позаказной системе производства однотипной продукции
Предположим, что цех получил задание на производство продукции не в штуках, а в виде заказов, включающих изделия, одинаковые по трудоемкости изготовления, но имеющие отличительные особенности. Например, различную окраску, комплектацию и т.д. Так может планироваться производство приборов разного рода, специального оборудования, автомобилей для экспорта и т.д.
Для простоты допусти, что речь идет о сборочном цехе и о производстве достаточно крупных изделий, объемы заказов которых исчисляются в штуках.
Пусть требуется выполнить следующие заказы: Z1=20, Z2=20, Z3=30, Z4=40, Z5=50, Z6=60.
Для их выполнения в цехе имеются три взаимозаменяемых сборочных линии, по которым заказы нужно распределить по возможности более равномерно, но в то же время не дробить заказы на части, т.к. это усложняет документацию и учет поставок продукции заказчику
Эта задача может быть отнесена к классу задач загрузки оборудования. При постановке её с применением математического программирования целевая функция может, например, иметь следующий вид:
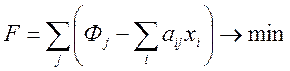 ,
(9.1)
,
(9.1)
где Фj – общий фонд времени работ j-го вида оборудования; xi – количество изделий i-го вида; aij – трудоемкость изготовления одного i-го вида изделия на j-ом оборудовании.
Таким образом, если даже не выполнять одно из требований задачи – не делить заказы на изделия, – то и в этом случае задача не может быть представлена в форме наиболее исследованной и имеющей стандартное ПО задачи линейного программирования.
Разность в выражении (9.1) может менять знак, что означает недогрузку или перегрузку оборудования. Это значит, что целевая функция не монотонна и её минимизация не имеет смысла.
Имеются эвристические методы решения этой задачи. Например, задаваясь Фj и xi и зная (из нормативно-справочной информации) aij, вычисляют фактическую трудоемкость изготовления всех изделий Tj, коэффициенты загрузки h, его пропускную способность η, перегрузку или недогрузку оборудования +∆xi и -∆xi. По их значениям судят о необходимости изменения xi. Процедура повторяется до тех пор, пока не получат приемлемые значения +∆xi и -∆xi.
В таком эвристическом алгоритме можно учесть больше факторов производственного процесса. Например, можно учесть коэффициенты смежности, износа и переналадки оборудования и т.п.
|
Ввод xi, Фj, aij |
|
|
|
|
|
|
|
|
|
|
|
η |
< 1 |
|
Дефицит
|
Резерв
|
|
Вывод η, h, -∆xi, +∆xi |
|
Рисунок 9.1
Рассмотрим возможность применения для решения этой задачи метода морфологического ящика (МЯ).
Сформируем из запасов морфологическую таблицу – МЯ (табл. 9.1).
Таблица 9.1
|
L |
A |
B |
|
Л1 |
Z1=10 |
Z4=40 |
|
Л2 |
Z2=20 |
Z5=50 |
|
Л3 |
Z3=30 |
Z6=60 |
Заказы объединены в группы: А=<Z1, Z2, Z3>, В=<Z4, Z5, Z6>.
Если приемлемое решение не будет получено, то МЯ можно переформировать, объединив заказы по-другому.
Таблица 9.2
|
L |
ZA |
ZB |
S |
Вариант решения |
||||||||
|
1 |
2 |
3 |
||||||||||
|
Л1 |
1 |
4 |
50 |
– |
– |
– |
||||||
|
Л1 |
1 |
5 |
60 |
+ |
+ |
– |
||||||
|
Л1 |
1 |
6 |
70 |
– |
– |
+ |
||||||
|
Л2 |
2 |
4 |
60 |
+ |
– |
– |
||||||
|
Л2 |
2 |
5 |
70 |
– |
– |
+ |
||||||
|
Л2 |
2 |
6 |
80 |
– |
+ |
– |
– |
|||||
|
Л3 |
3 |
4 |
70 |
– |
+ |
– |
+ |
|||||
|
Л3 |
3 |
5 |
80 |
– |
||||||||
|
Л3 |
3 |
6 |
90 |
+ |
– |
– |
– |
|||||
Для автоматизации перебора вариантов размещений с повторениями нужна автоматизация.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.