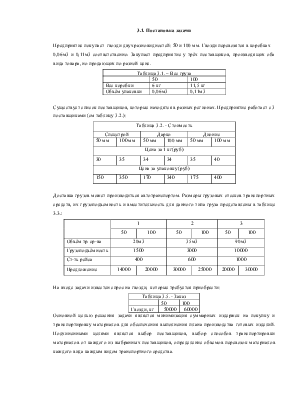

3.1. Постановка задачи
Предприятие покупает гвозди двух разновидностей: 50 и 100 мм. Гвозди перевозятся в коробках
0,06м3 и 0,11м3 соответственно. Закупает предприятие у трёх поставщиков, производящих оба вида товара, но продающих по разной цене.
|
Таблица 3.1. – Вес груза |
||
|
50 |
100 |
|
|
Вес коробки |
6 кг |
11,5 кг |
|
Объём упаковки |
0,06м3 |
0,11м3 |
Существует список поставщиков, которые находятся в разных регионах. Предприятие работает с 3 поставщиками (см таблицу 3.2.):
|
Таблица 3.2. - Стоимость |
|||||
|
Спецстрой |
Дарко |
Дионис |
|||
|
50 мм |
100 мм |
50 мм |
100 мм |
50 мм |
100 мм |
|
Цена за 1 кг(руб) |
|||||
|
30 |
35 |
34 |
34 |
35 |
40 |
|
Цена за упаковку (руб) |
|||||
|
150 |
350 |
170 |
340 |
175 |
400 |
Доставка грузов может производиться автотранспортом. Размеры грузовых отсеков транспортных средств, их грузоподъемность и вместительность для данного типа груза представлены в таблице 3.3.:
|
1 |
2 |
3 |
||||
|
50 |
100 |
50 |
100 |
50 |
100 |
|
|
Объём тр. ср-ва |
20м3 |
35м3 |
90м3 |
|||
|
Грузоподъёмность |
1500 |
3000 |
10000 |
|||
|
Ст-ть рейса |
400 |
600 |
1000 |
|||
|
Предложение |
14000 |
20000 |
30000 |
25000 |
20000 |
30000 |
На входе задачи известен спрос на гвозди, которые требуется приобрести:
|
Таблица 3.5. - Заказ |
||
|
50 |
100 |
|
|
Гвозди, кг |
50000 |
60000 |
Основной целью решения задачи является минимизация суммарных издержек на покупку и транспортировку материалов для обеспечения выполнения плана производства готовых изделий. Подчиненными целями является выбор поставщиков, выбор способов транспортировки материалов от каждого из выбранных поставщиков, определение объемов перевозок материалов каждого вида каждым видом транспортного средства.
3.2. Математическое описание
Введем следующие обозначения:
i – индекс поставщика ![]() , где I-количество поставщиков;
, где I-количество поставщиков;
j – индекс используемых материалов ![]() , где J- количество материалов;
, где J- количество материалов;
l – индекс вида транспортного средства
![]() , где L- количество видов транспортных средств ;
, где L- количество видов транспортных средств ;
Xijl – количество материала j, купленного у поставщика i и перевозимого транспортным средством l, ![]() ,
, ![]() ,
, ![]() ;
;
![]() – отпускная цена j–го материала у i–го поставщика;
– отпускная цена j–го материала у i–го поставщика;
![]() – цена за единицу транспорта l–го вида при перевозке груза от i –го поставщика;
– цена за единицу транспорта l–го вида при перевозке груза от i –го поставщика;
![]() – количество единиц транспортных
средств l–го вида, используемых для вывоза
материалов от i –го
поставщика;
– количество единиц транспортных
средств l–го вида, используемых для вывоза
материалов от i –го
поставщика;
![]() –
вместимость единицы транспортного средства l–го вида при перевозке материалов от i –го поставщика;
–
вместимость единицы транспортного средства l–го вида при перевозке материалов от i –го поставщика;
![]() –
грузоподъемность единицы транспортного средства l–го вида при перевозке материалов от i –го поставщика;
–
грузоподъемность единицы транспортного средства l–го вида при перевозке материалов от i –го поставщика;
![]() -
масса упаковки j вида
материала
-
масса упаковки j вида
материала
![]() – потребность в j–м материале.
– потребность в j–м материале.
Ограничения:
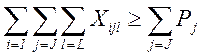 -
ограничение по спросу
-
ограничение по спросу
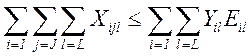 -
ограничение по вместимости транспортных средств
-
ограничение по вместимости транспортных средств
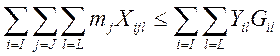 -
ограничение по грузоподъемности транспортных средств
-
ограничение по грузоподъемности транспортных средств
![]()
Целевая функция: 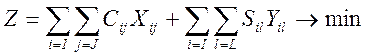
Описание последовательности действий, необходимых для получения результата
1. Перед запуском модели необходимо заполнить все исходные данные.
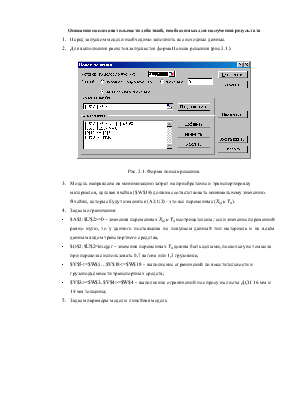
2. Для выполнения расчетов запускается форма Поиска решения (рис.3.1.)
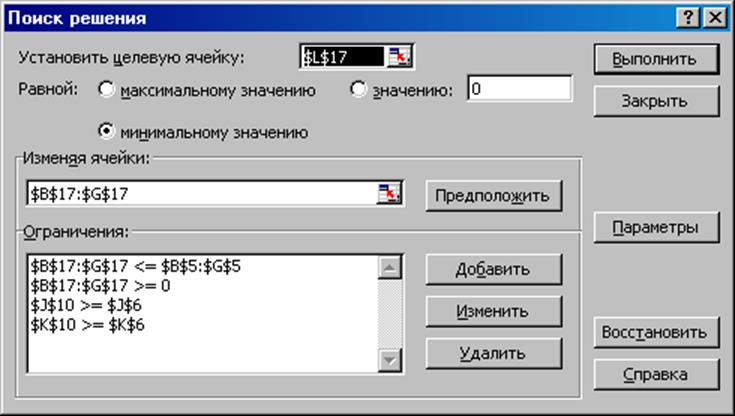
Рис. 3.1. Форма поиска решения.
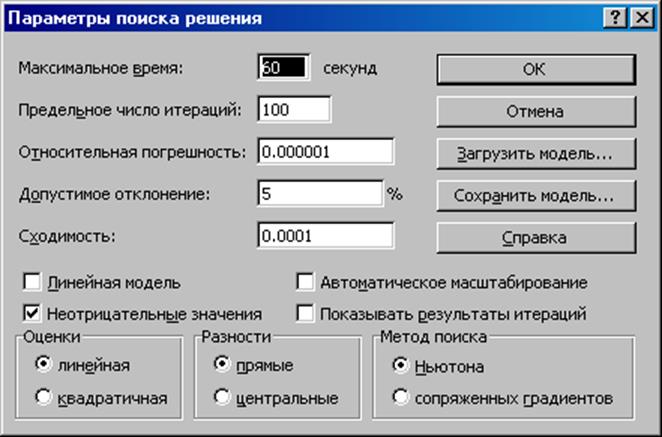
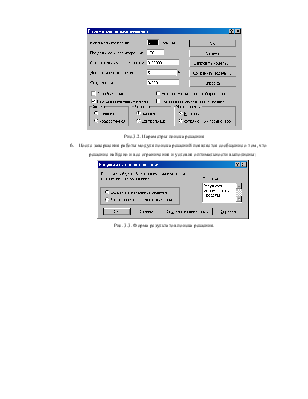
Рис.3.2. Параметры поиска решения
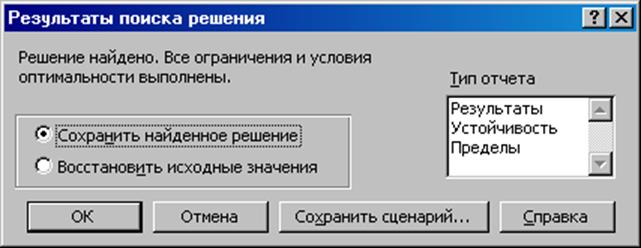
Рис. 3.3. Форма результатов поиска решения.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.