Министерство образования и науки Российской Федерации
Новосибирский государственный технический университет
Кафедра экономической информатики
Лабораторная работа № 1
Факультет: бизнеса
Группа: ФБИ-
Выполнили:
Проверил: Кириллов Ю.В.
Новосибирск
200
Цель работы:
· Приобрести практические навыки решения задач финансовой математики с помощью встроенных финансовых функций.
· Научиться решать задачи методом прямого счета.
Задание:
1. Расчет наращенной суммы
1.1. При постоянной процентной ставке
Задача. Какая сумма должна быть выплачена, если n лет назад была выдана ссуда Р тыс. руб. под j % годовых с ежемесячным начислением процентов?
|
Номер бригады |
Р, тыс. руб. |
n, лет |
i (j), % |
|
6 |
1500 |
6 |
15 |
Решение:
Поскольку, количество начислений в году 12, то есть m>1 используем понятие номинальной процентной ставки и рассчитываем наращенную сумму при постоянной процентной ставки следующим образом:
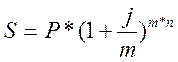 ,
,
где m – количество начислений в году,
n – количество лет начислений,
P – приведенная стоимость,
j – процентная ставка.
Кроме того, значение наращенной стоимости можно получить, выразив наращенную стоимость через приведенную, то есть
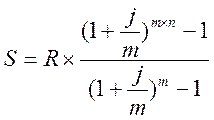 ,
,
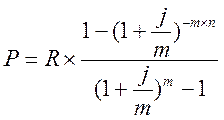
Таким образом,
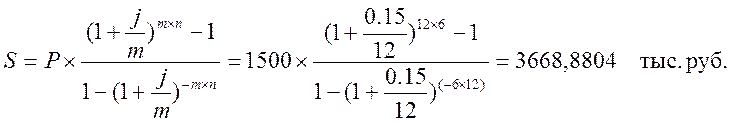


Данную задачу решим, используя встроенную функцию БС:
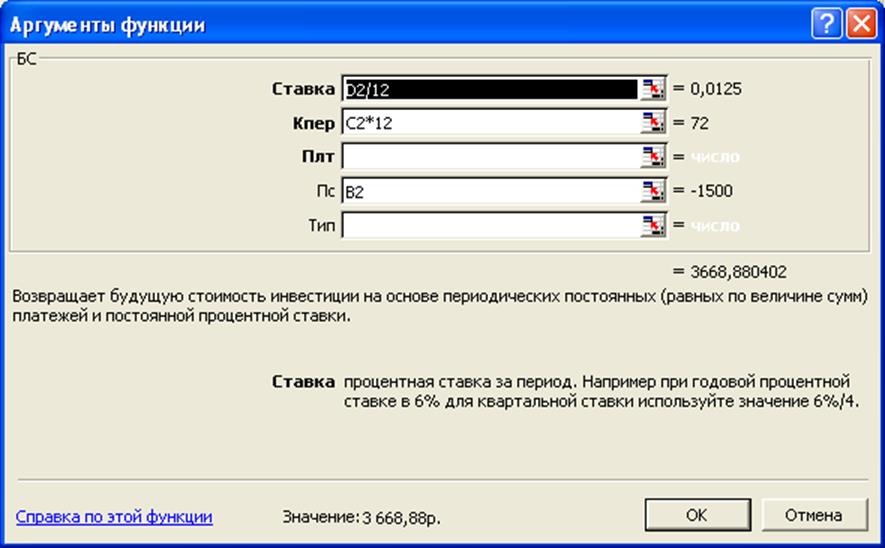
Анализ полученных результатов показывает, что значения наращенной суммы, рассчитанные как методом прямого счета, так и с помощью функции БС совпадают.
1.2. При переменной процентной ставке
Задача. Рассчитать будущую стоимость облигации номиналом Р тыс. руб., если предусмотрен следующий порядок начисления процентов: в первые n1 лет – i1 % годовых, в остальные n2 лет - i2 % годовых.
|
Номер бригады |
Р, тыс. руб. |
n1 , лет |
n2 , лет |
n3 , лет |
n4 , лет |
i1 % |
i2 % |
i3 % |
i4 % |
|
6 |
150 |
4 |
2 |
8 |
6 |
Решение
Наращенная сумма при переменной процентной ставки вычисляется по следующей формуле:
![]()

Данную задачу решим, используя встроенную функцию БЗРАСПИС:
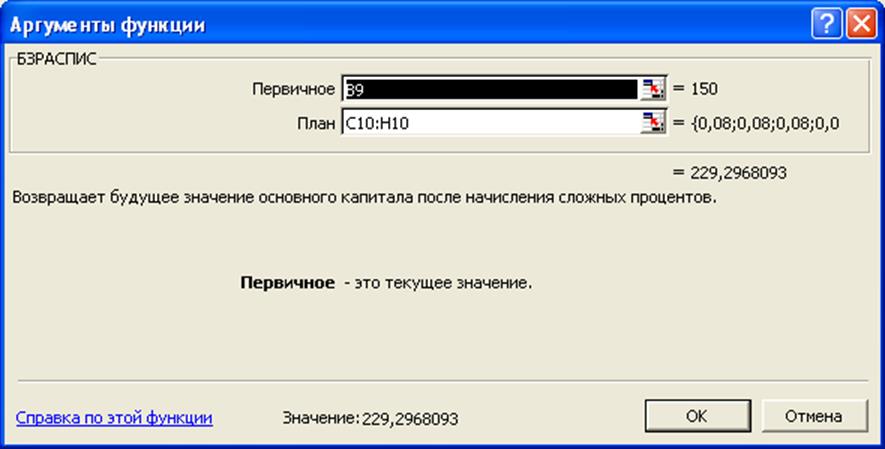
Анализ полученных результатов показывает, что значения наращенной суммы, рассчитанные как методом прямого счета, так и с помощью функции БЗРАСПИС совпадают.
2. Расчет приведенной стоимости
2.1. Для постоянного потока платежей
Задача. Определите текущую стоимость обязательных ежемесячных платежейс годовым размером R тыс. руб. в течение n лет, если начисление процентов производится ежеквартально по номинальной ставке – j % .
|
Номер бригады |
S, тыс. руб. |
R, тыс. руб. |
n , лет |
i (j) % |
|
6 |
120 |
4 |
14 |
Решение:
Поскольку, количество начислений в году 4, то есть m>1, используем понятие номинальной процентной ставки и рассчитываем приведенную сумму при постоянной процентной ставки следующим образом:
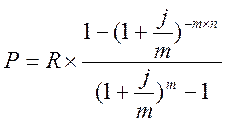
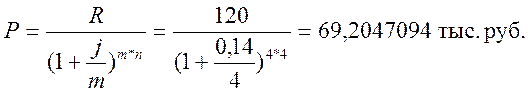

Данную задачу решим, используя встроенную функцию ПС:
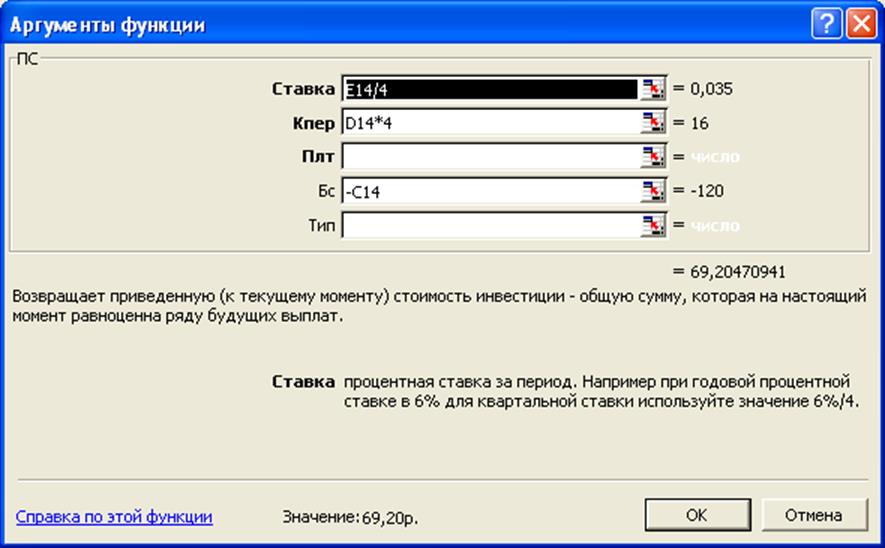
Анализ полученных результатов показывает, что значения наращенной суммы, рассчитанные как методом прямого счета, так и с помощью функции ПС совпадают.
2.2. Для переменного потока платежей
Задача. Рассматривается проект стоимостью K тыс. руб. Ожидается, что ежемесячные доходы составят D1 тыс. руб., D2 тыс. руб., D3 тыс. руб. и D4 тыс. руб. за четыре месяца. Определить эффективность проекта, если годовая норма процента i % .
|
Номер бригады |
K, тыс. руб. |
D1 тыс. руб. |
D2 тыс. руб. |
D3 тыс. руб. |
D4 тыс. руб. |
D5 тыс. руб. |
i % |
|
6 |
100 |
16 |
25 |
36 |
49 |
19 |
Решение
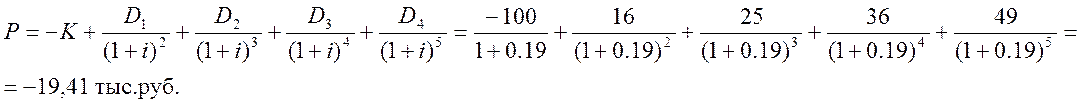

Данную задачу решим, используя встроенную функцию ЧПС:
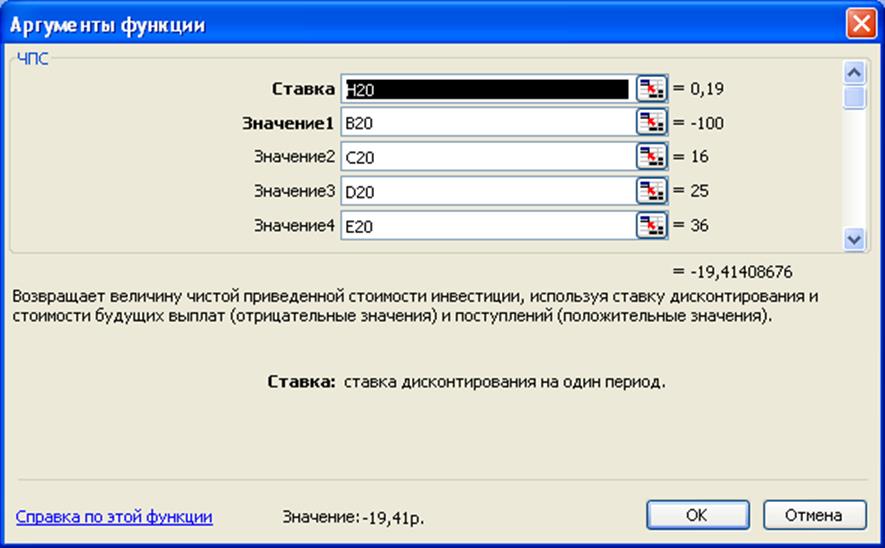
Анализ полученных результатов показывает, что значения наращенной суммы, рассчитанные как методом прямого счета, так и с помощью функции ЧПС совпадают.
2.3. Для нерегулярного потока платежей
Задача. Инвестиция размером K тыс. руб., сделанная 01.07.2003, принесет доходы: 15.09.2003 - D1 тыс. руб., 01.11.2003 - D2 тыс. руб., 01.01.2004 - D3 тыс. руб. и 01.03.2004 – D4 тыс. руб. Определите чистую приведенную стоимость инвестиций, если норма дисконтирования – i % годовых.
|
Номер бригады |
K, тыс. руб. |
D1 тыс. руб. |
D2 тыс. руб. |
D3 тыс. руб. |
D4 тыс. руб. |
i % |
|
6 |
20 |
2,75 |
4,25 |
5,5 |
8,6 |
9 |
Решение
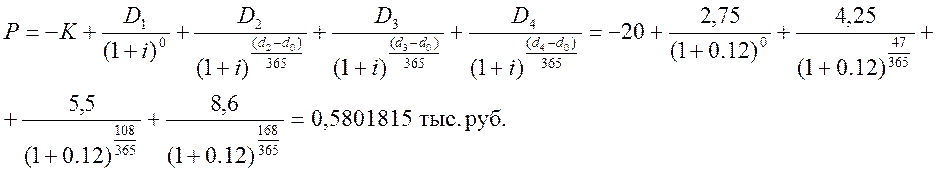

Данную задачу решим, используя встроенную функцию ЧИСТНЗ:
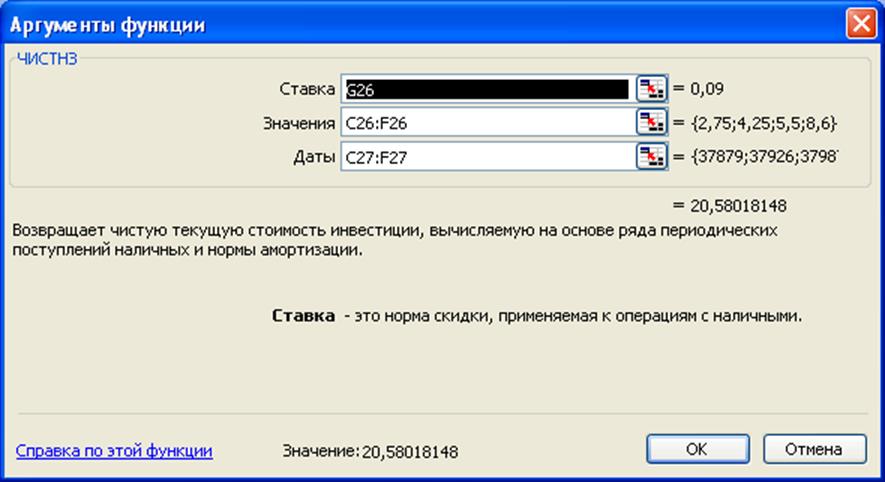
Анализ полученных результатов показывает, что значения наращенной суммы, рассчитанные как методом прямого счета, так и с помощью функции ЧПС совпадают.
4. Определение срока платежа и процентной ставки
4.1. Срок постоянного потока платежей
Задача. Рассчитать, через сколько месяцев вклад размером P тыс. руб. достигнет величины S тыс. руб. при ежемесячном начислении процентов по ставке – j % годовых.
|
Номер бригады |
S, тыс. руб. |
R, тыс. руб |
P, тыс. руб. |
i (j) % |
|
6 |
10000 |
200 |
16 |
Решение
Так как
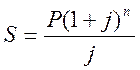 , то
, то
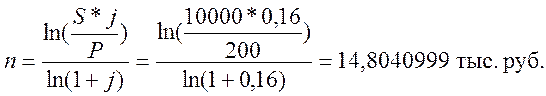

Данную задачу решим, используя встроенную функцию КПЕР:
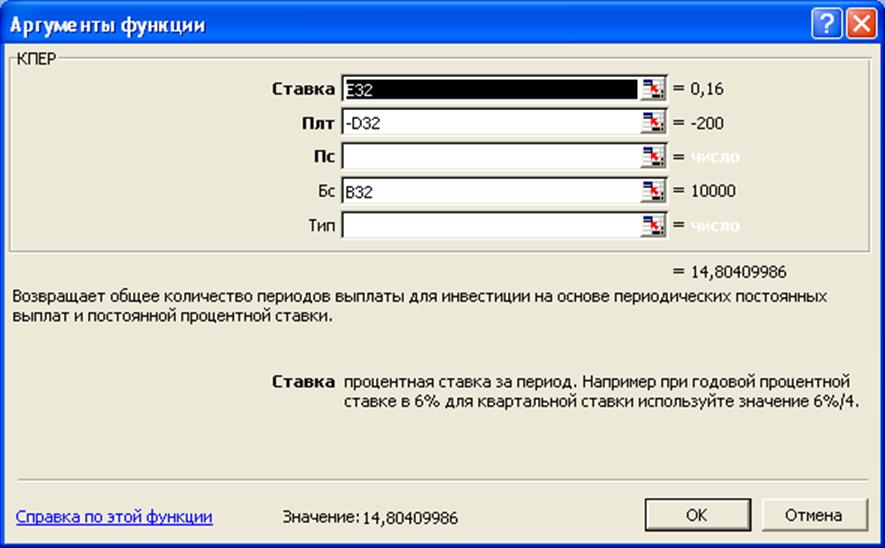
Анализ полученных результатов показывает, что значения наращенной суммы, рассчитанные как методом прямого счета, так и с помощью функции КПЕР совпадают.
4.2. Процентная ставка
Задача. Фонд размером S тыс. руб. был сформирован за n лет за счет годовых отчислений по R тыс. руб. в начале каждого месяца. Определить годовую ставку процента.
|
Номер бригады |
S, тыс. руб. |
R, тыс. руб. |
P, тыс. руб. |
n, лет |
|
6 |
21000 |
770 |
2 |
Решение

Данную задачу решим, используя встроенную функцию СТАВКА:
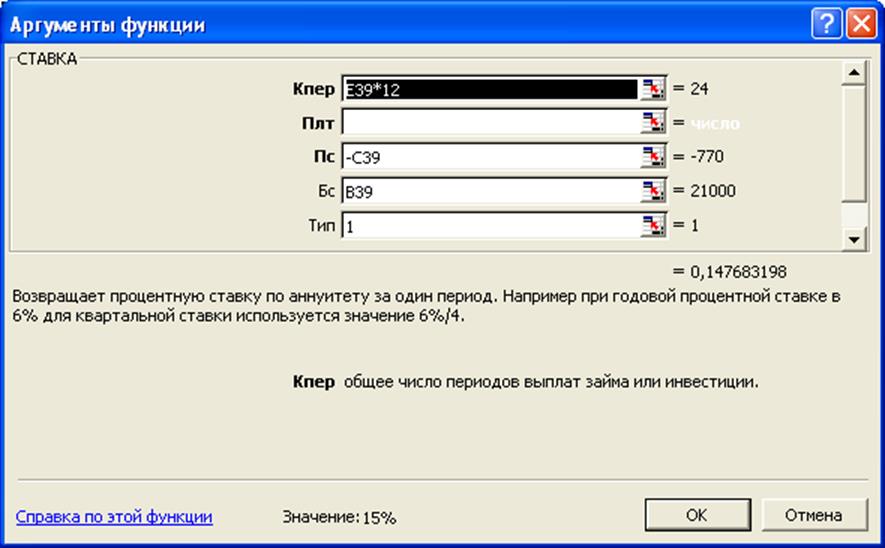
Анализ данной задачи показывает, что значения наращенной суммы, рассчитывается с помощью функции СТАВКА.
5. Расчет эффективной процентной ставки и размера платежа
5.1. Эффективная ставка
Задача. Заем в сумме P тыс. руб. взят сроком на n лет с номинальной ставкой j %. Найти эффективную ставку при начислении процентов m в год.
|
Номер бригады |
P, тыс. руб. |
j % |
m |
n, лет |
|
6 |
10000 |
12,3 |
2 |
4 |
Решение
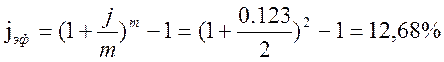

Данную задачу решим, используя встроенную функцию ЭФФЕКТ:
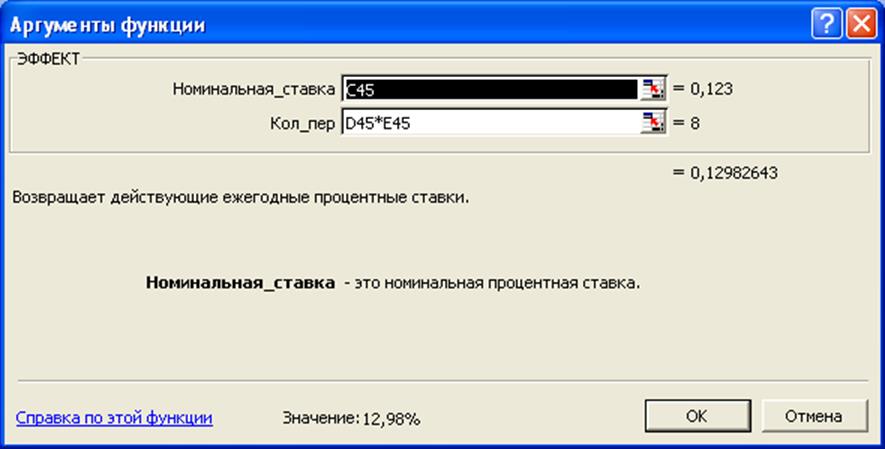
Анализ полученных результатов показывает, что значения наращенной суммы, рассчитанные как методом прямого счета, так и с помощью функции ЭФФЕКТ совпадают.
5.2. Размер платежа постоянной ренты
Задача. Банк выдал ссуду в размере P тыс. руб. на n лет под j % годовых. Погашение производится одинаковыми платежами каждые полгода. Определите размер платежа, если начисление процентов – полугодовое?
|
Номер бригады |
S, P, тыс. руб. |
n , лет |
j % |
|
6 |
1500 |
6 |
15 |
Решение
Так как m=p, то используем следующую формулу:
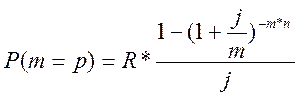
Из данной формулы находим R:
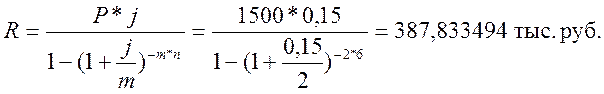
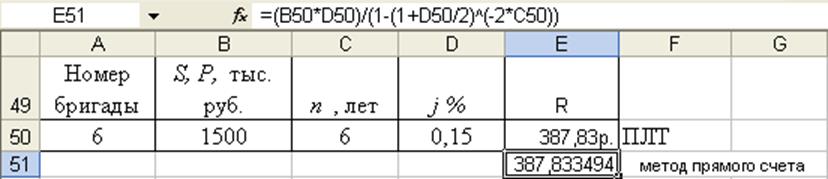
Данную задачу решим, используя встроенную функцию ПЛТ:
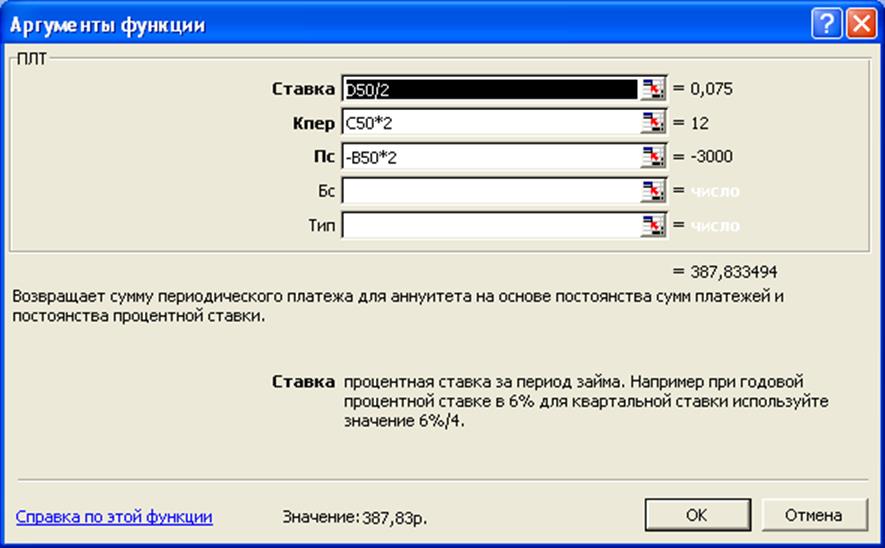
Анализ полученных результатов показывает, что значения наращенной суммы, рассчитанные как методом прямого счета, так и с помощью функции ПЛТ совпадают.
Вывод:
В ходе лабораторной работы были приобретены практические навыки решения задач финансовой математики, как с помощью встроенных финансовых функций, так и методом прямого счета.
Был проведен расчет наращенной суммы при постоянной и переменной процентных ставках, приведенной стоимости для постоянного, переменного, нерегулярного потоков платежей, срока платежа и процентной ставки, эффективной процентной ставки, размер платежа постоянной ренты.
Анализ результатов показывает, что значения полученные как методом прямого счета, так и с помощью встроенных финансовых функций совпадают.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.