где r (r) - число атомов в единице объема шарового слоя. Иначе эта величина равна
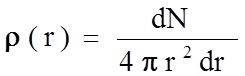(1.8.3)
где dN - число атомов в выделенном
шаровом слое с радиусами от r до r+dr.
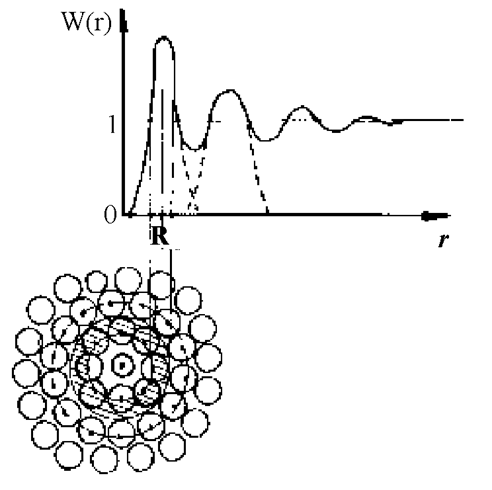
Рис.1.8.1. Вид функции радиального распределения для аморфного твердого тела
Из формулы (1.8.2) следует, что величина
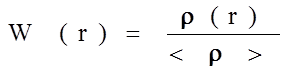
показывает, во сколько раз отличается истинное количество атомов в единице объема от средней атомной плотности. Домноженная на массу m одного атома величина <r> дает обычную табличную плотность вещества. Если умножить mr(r) на объем сферы радиусом R, то получим величину g(R) - массы заключенной в этом объеме. Экспериментальные данные часто представляют в виде графиков зависимостей g=g(r) (например, рис.1.8.2) или зависимостей от r величины 4pr2 [r(r) - <r>], дающей представление об отклонении плотности от ее среднего значения (рис.1.8.3).
Ход кривых рассчитывается из экспериментальных данных с помощью Фурье - преобразования интенсивности почернения фотопластинки, полученной при изучении интерференции на аморфном объекте рентгеновских лучей, электронов или нейтронов, измеренной с помощью спектрофотометра.
Функция радиального распределения обладает рядом свойств:
1.Она пропорциональна плотности вещества r(г) и потому имеет осциллирующий вид.
2. Она максимальна вблизи значений г, соответствующих наиболее вероятным межатомным расстояниям и проходит через минимумы между этими положениями.
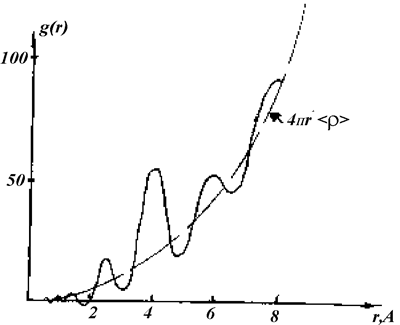
Рис.1.8.2. ФРР атомной плотности в соединении GeTe.
 |
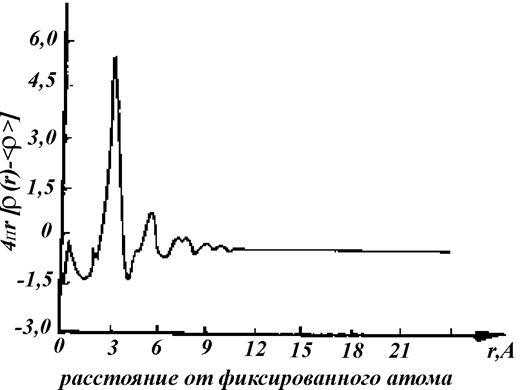Рис. 1.8.3. ФРР металлического стекла (Pt0,8Ni0,2)73P27
4. При изменении внутреннего строения тела вид ФРР изменяется, но он не зависит от позиции атома, взятого за начало отсчета.
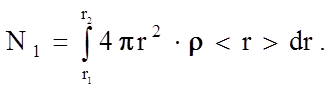5. По величине площади
под максимумом кривой ФРР можно определить координационное число. Из
определения атомной плотности и формулы (1.8.3) следует, что число атомов в
соответствующих координационных сферах равно N1
или N2, определяется путем интегрирования:
(1.8.4)
О координационных сферах большего порядка в аморфных телах нет смысла говорить, так как упорядоченность в расположении атомов не сохраняется.
Как правило, в моноатомных аморфных структурах координационное число первой сферы соответствует данным, получаемым при исследовании кристаллической модификации того же вещества. Второе координационное число хуже совпадает со значениями для кристаллов. Вычисленные значения - обычно дробные числа. Расчет этих значений позволяет делать предположение не только о пространственной структуре исследуемых веществ, но и уточнять, какие атомы являются соседними, что особенно важно для двух- и многоатомных соединений.
6. Ширина максимумов на половине высоты характеризует среднеквадратичные отклонения атомов от равновесных положений и интенсивность их теплового движения. Чем меньше ширина максимумов, тем меньше отклонение.
Достаточно глубоко исследованы ФРР для полупроводниковых аморфных материалов - Ge, Si, Se, Тe, для сплавов металлов с интересными магнитными, химическими и механическими свойствами. Для объяснения получаемых результатов часто применяется моделирование структуры и расчет рассеяния на модели с помощью ЭВМ. Используются модели: микрокластеров (иногда их называют аморфонами), в которых пространственные конфигурации составляются из пяти- или шестизвенных колец и групп, а также модель непрерывной сетки, состоящей из атомов (молекул) или небольших одинаковых групп. Например, в модели для аморфного углерода длины межатомных связей колеблются около среднего значения до ± 1%, а углы между связями могут отклоняться от средних значений до 20°. Эти вариации позволяют «сшить» кластеры друг с другом без заметных пустот.
Интересно и необходимо отметить, что методами машинного моделирования показана возможность подбора конфигураций атомных групп, приводящих к удовлетворительному согласию эксперимента по определению ФРР не только с этими двумя "опорными" моделями.
Описание структуры индивидуальных аморфных тел предполагает количественное определение ряда параметров:
1) длин химических связей и характерных расстояний до ближайших и более удаленных атомов;
2) валентных углов между связями, что в сочетании с ковалентными и ван-дер-ваальсовыми радиусами ионов позволяет построить пространственные модели молекул и комплексов, из которых состоит структура тела;
3) координационных чисел и равновесных расстояний фиксированной молекулы (группы) до ее ближайших соседей.
 |
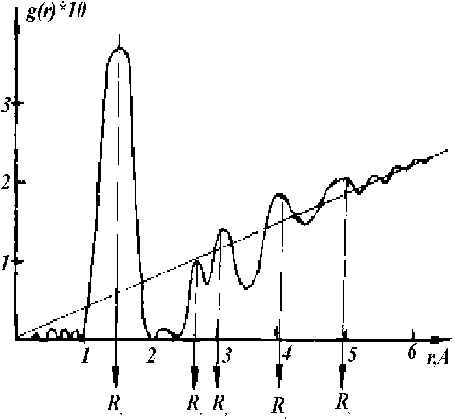Рис. 1.8.4. Распределение функции пар атомов в SiO2. R1, R2, R3, R4, R5 - положения максимумов, соответствующие межатомным расстояниям Si-O, Si-Si, O-O
Последние сведения требуют преодоления некоторых математических трудностей, связанных с невозможностью прямого применения Фурье-преобразований. Предложенная Б.Уорреном замена ФРР атомов на ФРР электронов позволила ему получить уравнение, примененное впервые для анализа проектных силикатных и боратных стекол, а теперь широко применяемое для описания ближнего порядка в жидкостях и аморфных твердых телах.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.