Физические основы рентгеновских, электронно-микроскопических, электронографических и нейтронографических методов исследования структуры твердых тел

3.1. ФИЗИЧЕСКИЕ ОСНОВЫ РЕНТГЕНОВСКИХ, ЭЛЕКТРОННО-МИКРОСКОПИЧЕСКИХ, ЭЛЕКТРОНОГРАФИЧЕСКИХ И НЕЙТРОНОГРАФИЧЕСКИХ МЕТОДОВ ИССЛЕДОВАНИЯ СТРУКТУРЫ ТВЕРДЫХ ТЕЛ

Дифракция рентгеновских волн (фотонов)  и волн де Бройля, свойственных движущимся электронам, нейтронам, протонам и ионам, является той физической основой, которая позволяет определять периодическое расположение атомов в кристаллах, их колебания, перестройку при различных внешних воздействиях и изменениях физического состава. Волновые свойства потоков этих частиц, включая фотоны оптического диапазона, используются и при проведении анализа химического состава веществ как методами традиционного спектрально-дугового анализа, так и в  современных методах рентгеновского флуоресцентного и рентгеновского электронно-зондового микроанализа.

При более тонких исследованиях состояния поверхности твердых тел используется дисперсия по энергиям медленных электронов (ДМЭ или LLED) и высокоэнергетичных электронов (ДВЭ или HEED), ОЖЕ-спектроскопия, основанная на изучении спектров излучения, возникающих при возбуждении внешних валентных электронов, а также ЭСХА-электронная спектроскопия для химического анализа, при которой возбуждается мягкое рентгеновское характеристическое излучение. Эти методы требуют высокого вакуума (10^-9...10^-11 мм рт. ст.).

Некоторые косвенные данные о длинах волн излучения, открытого в 1890 году Конрадом Рентгеном, указывали, что они близки к периодам кристаллических решеток (~1Å  = 10^-8 см). В 1912 году Лауэ предложил использовать для рентгеновских лучей в качестве дифракционных решеток кристаллы с регулярным расположением атомов. Опыт подтвердил достоверность предположения, и одновременно родились две гипотезы: о волновой природе рентгеновских лучей и о регулярном расположении атомов в кристаллической решетке.

          Р е н т г е н о в с к и е   л у ч и   составляют часть спектра электромагнитного излучения с длинами волн в пределах от l = 10Å ("мягкое" рентгеновское излучение) до l = 0,01 Å  ("жесткое" рентгеновское излучение). В средине диапазона, при  l = 1Å , энергия кванта составляет ~ 10  эВ. Рентгеновские волны могут излучаться как при торможении электронов или других частиц мишенями (обычно металлическими), так и при неупругом возбуждении электронов с глубоких внутренних уровней атомов мишени. Первый процесс дает широкий непрерывный спектр, второй приводит к узким линиям характеристического излучения (рис.3.1.1).

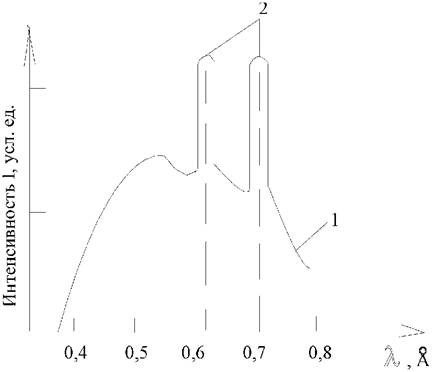Рис.3.1.1.Спектр рентгеновского излучения, полученный от трубки с молибденовым антикатодом при напряжении U = 35 кВ: 1 - непрерывный спектр, 2 - К_a и К_b - линии характеристического излучения

Для исследования кристаллов требуется рентгеновское излучение с энергией квантов e от 10 кэВ  до 50 кэВ, откуда по уравнению 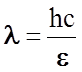 можно найти длину волны  (h = 6,62×10^-34 Дж×с  - постоянная Планка, с = 3×10⁸ м/с - скорость света, 1 эВ = 1,6×10^-19 Дж).  В практических целях длину волны квантов в ангстремах удобно определять по формуле

l(Å) =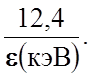                                                                     (3.1.1)

Э л е к т р о н ы. Длина волны де Бройля для нерелятивистского электрона связана с его импульсом р_е  и энергией соотношением 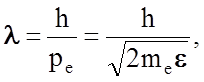 где m_e = 9,11×10^-31 кг - масса электрона, h – постоянная  Планка. В более употребительных в микромире единицах

l(Å ) »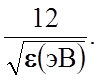                                                                     (3.1.2)

Дифракция электронов на кристаллической решетке, предсказанная де Бройлем в 1924 году, экспериментально подтверждена опытами Дэвиссона и Джермера в 1927 году. С тех пор она широко применяется при структурном анализе. Из-за большого потенциального барьера для электронов на поверхности твердого тела  глубина проникновения электронов с энергией порядка 1 кэВ невелика. Дифракция таких электронов, называемых медленными (ДМЭ или LEED), происходит на поверхностных атомах, что позволяет изучать не только расположение атомов в поверхностных слоях, но и адсорбцию в поверхностном слое, в частности, атомов кислорода или других атомов атмосферы.

При больших скоростях с помощью пучка электронов можно исследовать кристаллические и аморфные пленки на просвет и на отражение.

Н е й т р о н ы. Длина волны де Бройля l для нейтронов связана с их импульсом р_n и энергией e  формулой 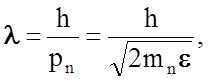где m_n = 1,675×10^-27 кг - масса нейтрона. 

Используя для измерения энергии нейтрона электрон-вольты, а длин волн - ангстремы (Å ), можно записать

l(Å ) » 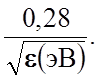                                                                    (3.1.3)

Например, l = 1 Å  соответствует энергия e » 0,08 эВ. В немагнитных материалах нейтроны взаимодействуют с ядрами атомов, образующих решетку. Измеряя их рассеяние, можно не только определять координаты атомов и тип решеток или параметры аморфной структуры, но и изучать интенсивность тепловых колебаний решеток. Наличие же у нейтронов магнитного момента позволяет исследовать магнитную структуру веществ, вследствие сильного взаимодействия медленных нейтронов с "магнитными" электронами твердого тела.

3 а к о н   В у л ь ф а - Б р э г г а.  В 1913 году английские братья Брэгг и независимо от них русский ученый Вульф получили уравнение, описывающее дифракцию рентгеновских лучей в кристаллах

2d×sin q = nl.                                                                          3.1.4)

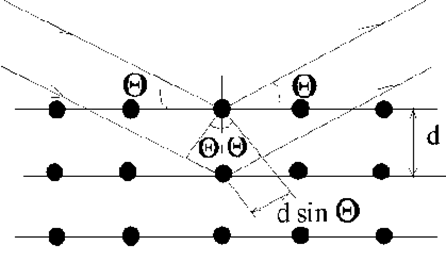
          Рис.3.1.2.Иллюстрация к закону Вульфа-Брэгга: d  - межплоскостное расстояние, q - угол скольжения

Рассмотрим семейство равноотстоящих плотноупакованных атомных плоскостей в идеальном кристалле (рис.3.1.2).

Если межплоскостное расстояние равно d, то для двух лучей, отраженных от последовательных плоскостей, разность хода составит 2d×sinq, где q - угол скольжения, отсчитываемый от атомной плоскости. Излучение, отраженное от соседних плоскостей, будет при интерференции усиливаться (и, следовательно, наблюдаться) в том случае, когда разность хода будет равна целому числу n длин волн l. Уравнение (3.1.4) справедливо лишь при l £ 2d, а потому для волн оптического, видимого диапазона применительно к кристаллам не выполняется. Но оно выполняется, если в уравнение (3.1.4) подставлять длины волн из уравнений (3.1.2) и (3.1.3) для электронов, нейтронов и подобным образом полученных длин волн Де Бройля для любых микрочастиц.

Например, при нормальном падении пучка электронов на решетку с параметром d под углом j, определяемым уравнением

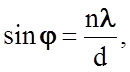                                                                            (3.1.5)

будет наблюдаться дифракционный максимум отражения электронов, если их длина волны Де Бройля будет удовлетворять соотношению (3.1.2) 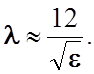 Если электроны ускорялись электрическим полем, то e = qU, где q = 1,6×10^-19 Кл - заряд электрона, а U – ускоряющее напряжение,  l(Å ) =

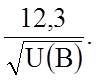
Кроме того, при точным анализе результатов взаимодействия зондирующих потоков квантов и частиц с веществом приходится учитывать ряд тонких факторов: электронное строение атомов и ионов, образующих решетку; возможность комптоновского рассеяния; фотоионизацию; температурные зависимости интенсивностей рассеяния; наличие проводящих или, наоборот, непроводящих пленок на исследуемой поверхности; ослабление отраженной волны вследствие эффектов экстинкции, связанных с многократностью взаимодействия падающего потока с параллельно расположенными слоями.