Триггеры: Методическое пособие по курсу «Цифровая техника и микропроцессоры», страница 2

Для синтеза схемы триггера составим карту Карно:

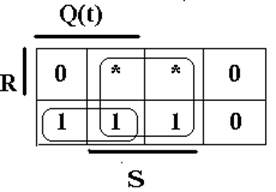
По карте записываем минимальную ФАЛ – логическое уравнение RS-триггера, которое полностью описывает его работу:

         Q(t+1) = S + R Q(t)                         (1)

Реализуем триггер на элементах И-НЕ, для чего переведем запись логического уравнения в базис И-НЕ, используя правило де-Моргана:

 

  Q(t+1)=S+ R Q(t)= S+ R Q(t)= S * R Q(t)            (2)

Несмотря на кажущуюся простоту, рассмотрим получение схемы триггера поэтапно.

Зададим исходно три  цифровых сигнала(три линии):

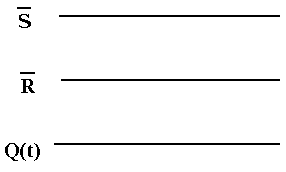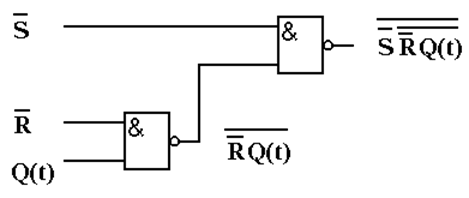
Реализуем член       уравнения (2):

Реализуем всю правую часть уравнения (2):

     На выходе схемы получен сигнал Q(t+1), являющийся новым значением сигнала Q(t). Это означает, что мы должны соединить эти точки. Для учета того факта, что это один и тот же сигнал, но в разные моменты времени, соединение допустимо выполнить только через некоторое устройство временной задержки:      

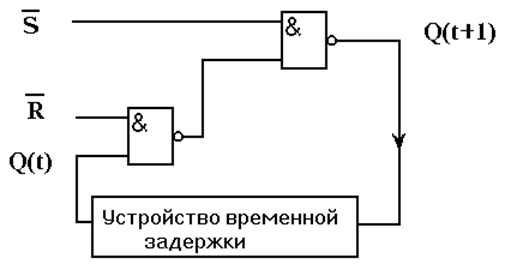И последний шаг. Из-за наличия реактивностей в реальном логическом  элементе сигнал на его выходе изменяется не одновременно со входным, а спустя некоторое время. Поэтому введенное устройство задержки можно спокойно удалить, полагая Q(t+1) = Q(t), и получить окончательную схему асинхронного RS-триггера на двухвходовых элементах И-НЕ:

 

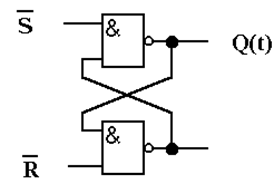
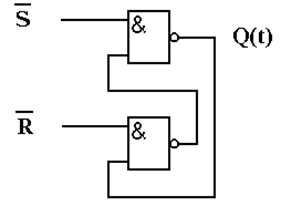
или в более

наглядном виде с  характерными пере-

крестными связями:

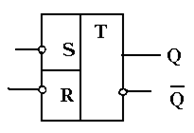Можно показать, что сигнал на нижнем выходе будет всегда инверсией сигнала Q(t), за исключением случая подачи на входы триггера комбинации  S = R = 1 – здесь сигналы будут одинаковы. Полезно самостоятельно в этом убедиться, расставив по схеме сигналы во всех точках. 

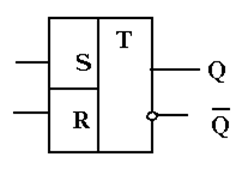
     Синтезированный простейший триггер                         

     на  схемах   обычно изображают  в    

     виде прямоугольника, опуская  его    

     внутреннюю структуру.

     Обратите внимание на то, что управляющим действием обладают нулевые уровни входных сигналов, что отражено кружками – символами инверсии – на входных линиях. Это присуще RS-триггеру, собранному именно на элементах И-НЕ.

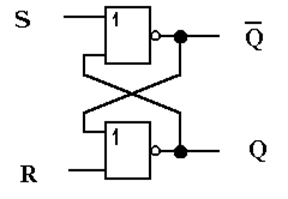
     Согласно принципу двойственности логических схем, при сохранении ее структуры и замене элементов И-НЕ на элементы ИЛИ-НЕ и наоборот, принцип работы схемы не нарушится. Необходимо лишь инвертировать все сигналы (как входные, так и выходные), чтобы для внешнего наблюдателя работа схемы казалась неизменной. Поэтому можно изобразить схему RS-триггера на элементах ИЛИ-НЕ так:

   или

Обратите внимание на отсутствие символов инверсии на входных проводниках вследствие проведенной инверсии всех сигналов. Это означает, что работа RS-триггера, собранного на элементах ИЛИ-НЕ, полностью соответствует вышеприведенной исходной таблице истинности (без необходимости инверсии столбцов входных сигналов), т.е. управляющем действием обладают единичные уровни входных сигналов.

     Повторим, что в литературе для такого триггера входную комбинацию S = R = 1 называют запрещенной. Многие понимают эту фразу в прямом смысле и считают, что такую комбинацию на вход триггера подавать нельзя. Это ошибочное мнение. Для доказательства расставим сигналы во всех точках схемы при таком воздействии:

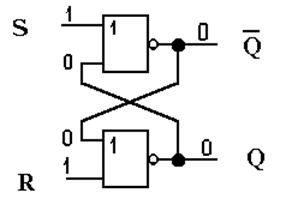Нетрудно видеть, что триггер находится в устойчивом состоянии, правда, несколько необычном – оба выходных сигнала равны нулю. Неискушенный читатель воскликнет: – «Не может быть! Эти сигналы у триггера всегда инверсны!»

Увы, он неправ. Указанное состояние триггер будет поддерживать сколь угодно долго – пока сохраняется S=R=1.

Тогда в чем же мнимая “запрещенность” такой комбинации?

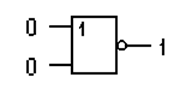     Ответ довольно прост. Предположим, что мы одновременно изменили входные сигналы на S = R = 0, желая перейти в режим хранения. Этим мы предоставили схеме полную свободу действий, и она не останется в прежнем состоянии по выходам. Действительно, наличие двух нулей на входе элемента ИЛИ-НЕ обеспечивает единицу на выходе:

Эта единица подается на вход соседнего элемента, заставляя того оставаться  в нуле:

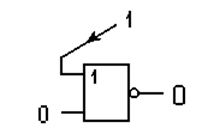Вопрос – какой элемент из двух переключится по выходу в единицу, а какой останется в нуле? Точное состояние предсказать невозможно, поскольку более “быстрый” элемент побежит вперед, оставляя “соперника” в прежнем состоянии. Скорость работы зависит от технологии изготовления (концентрации примесей в полупроводнике и.т.п.). Несмотря на то, что оба элемента ИЛИ-НЕ  - “близнецы” и даже расположены на одном кристалле, их свойства никогда не будут абсолютно идентичны. 

     Вывод ко всему сказанному:  “запрещенность” комбинации S = R = 1 состоит лишь в том, что после ее снятия и одновременной замены на S = R = 0, состояние триггера по выходам нельзя указать однозначно. Неучет этого фактора может привести к нарушению работы цифровой схемы, где есть такие триггеры.

     В заключение составим так называемую таблицу возбуждения RS-триггера, которая нам пригодится в дальнейшем. Она составляется по таблице истинности и фактически копирует ее в сокращенном виде.   

     Таблица возбуждения триггера показывает, какие сигналы необходимо подать на  управляющие входы для изменения выходного сигнала. Поэтому в таблице возбуждения любого триггера всегда 4 строки, соответствующие всевозможным вариантам изменения выходного сигнала:

Q(t) – было	....	...	Q(t+1)–стало
0	...	...	0
0	...	...	1
1	...	...	0
1	...	...	1

Количество средних столбцов таблицы определяется числом входных управляющих сигналов триггера. Для RS-триггера исходно имеем шаблон таблицы возбуждения:

Q(t) – было	S	R	Q(t+1)–стало
0			0
0			1
1			0
1			1

Заполним шаблон, глядя на таблицу истинности триггера. Согласно этой таблице, переход  0 -> 0  обеспечивает любая из двух комбинаций входных сигналов:

           S = 0     или       S = 0