Терминология цифровых фильтров, страница 3

Фильтр (для) децимации (Decimation Filter) – цифровой фильтр нижних частот с конечной импульсной характеристикой (КИХ-фильтр), у которого выходная скорость отсчетов меньше, чем входная. Для избежания проблем связанных с элайзингом (наложением спектров) выходная скорость отсчетов не должна нарушать критерия  Найквиста.

Полуполосовой фильтр (Half-band filter) – тип КИХ-фильтра, у которого переходная область центрирована  около четверти частоты отсчетов, или . В частности, конец полосы пропускания и начало полосы задерживания приходятся на два участка, примыкающие к частоте . Такие фильтры часто используются в фильтрации для децимации (прореживания), поскольку (почти) половина коэффициентов во временной области в них является нулевой. Это значит, к примеру, вы можете получить характеристики M-элементного фильтра с конечной импульсной характеристикой при вычислительных затратах 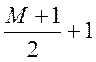 умножений на отсчет выходного сигнала фильтра.

Фильтр нижних частот (ФНЧ, Low-pass filter) – фильтр, который пропускает низкие частоты и ослабляет высокие, как показано на рисунке 6. Например,  мы сталкиваемся с низкочастотной фильтрацией, когда увеличиваем нижние звуковые частоты (или ослабляем высокие звуковые частоты) на наших домашних стереосистемах, так как низкочастотные компоненты музыки становятся более интенсивными.

Фильтр с бесконечной импульсной характеристикой (БИХ-фильтр, Infinite Impulse Response Filter) – определяет класс цифровых фильтров, которые могут иметь и нули и полюса в z-плоскости. БИХ-фильтры не обязательно являются устойчивыми и в большинстве своем имеют нелинейную фазовую характеристику. Для определенного порядка БИХ-фильтры имеют более крутую переходную область спада амплитудно-частотной характеристики, чем КИХ-фильтры.

Фильтр с конечной импульсной характеристикой (КИХ-фильтр, Finite Impulse Response (FIR) Filter) – определяет класс цифровых фильтров, у которых существуют только нули в z-плоскости. Главным следствием этого является то, что КИХ-фильтры всегда устойчивы и имеют линейную фазовую характеристику (до тех пор, пока коэффициенты фильтра симметричны). Для определённого порядка КИХ-фильтры имеют гораздо более плавный спад в переходной области, чем цифровые БИХ-фильтры.

Фильтр с линейной фазой (Linear Phase Filter) – фильтр, который имеет постоянное изменение  фазы выходного сигнала в зависимости от частоты. Результирующий график фазы от частоты является прямой линией. По существу, групповая задержка фильтра линейной фазы является постоянной. Линейность фазы является важным критерием для фильтров, используемых в коммуникационных системах.

Форм-фактор (коэффициент формы (кривой), Shape Factor) – термин используется для определения  крутизны спада характеристики фильтра. Форм-фактор обычно определяется как отношение ширины полосы пропускания фильтра плюс ширина переходной области к ширине полосы пропускания. Для идеального фильтра область перехода имеет нулевую длину, а форм-фактор равен единице. Термин форм-фактора очень долго использовался в радиочастотной(RF) области для описания аналоговых фильтров, и определялся как отношение ширины полосы пропускания фильтра на  уровне 60 ДБ к ширине полосы пропускания на  уровне 3 ДБ.

Функция Баттерворта (Butterworth Function) – математическая функция, используемая для получения максимально плоской амплитудной характеристики фильтра без рассмотрения линейности фазы или изменений групповой задержки. У фильтра, спроектированного на основе функции Баттерворта, нет пульсаций амплитуды как в полосе пропускания, так в полосе задерживания (полосе затухания). К сожалению, фильтры Баттерворта определенного порядка (filter order) имеют самую широкую переходную область среди самых популярных функций проектирования фильтров.

Функция Бесселя (Bessel Function) – математическая функция, используемая для получения наиболее линейной фазовой характеристики у БИХ-фильтров. Более точно – фильтр, спроектированный с помощью функции Бесселя, имеет максимально постоянную групповую задержку.

Функция Чебышева (Chebyshev Function) – математическая функция, используемая для получения фильтров с неравномерностями в полосе пропускания или полосе задерживания. Фильтры Чебышева могут быть спроектированы так, что частотная характеристика будет с пульсациями в полосе пропускания и плоской полосой задерживания (фильтры Чебышева первого порядка) или с плоской полосой пропускания и пульсациями в полосе задерживания (фильтры Чебышева второго порядка). Фильтры Чебышева не могут иметь пульсаций в полосе пропускания и полосе задерживания одновременно. У цифровых фильтров, построенных на основе функций Чебышева, более крутой спад в переходной области, но более нелинейная фазовая характеристика, чем, скажем, у фильтров Баттерворта.

Центральная частота ( Center Frequency) – частота, лежащая в средней точке полосового фильтра. На рис.5 обозначена   - центральная частота полосового фильтра.

Цифровой фильтр (Digital Filter) – вычислительный процесс или алгоритм, преобразующий дискретную последовательность чисел (входной сигнал) в другую дискретную последовательность чисел (выходной сигнал) с изменённым частотным спектром. Цифровая фильтрация может быть реализована в виде программы, оперирующей с данными, хранящимися в памяти компьютера, или может быть осуществлена с помощью предназначенного для этого специального  цифрового оборудования.

Частота среза (граничная частота, Cutoff Frequency) – наивысшая частота полосы пропускания фильтров нижних частот или низшая частота полосы пропускания фильтров высоких частот. Частота среза определяется в точке при спаде на 3ДБ амплитудной характеристики фильтра относительно максимума полосы пропускания. На рис.7 изображена точка  - частота среза фильтра нижних частот.

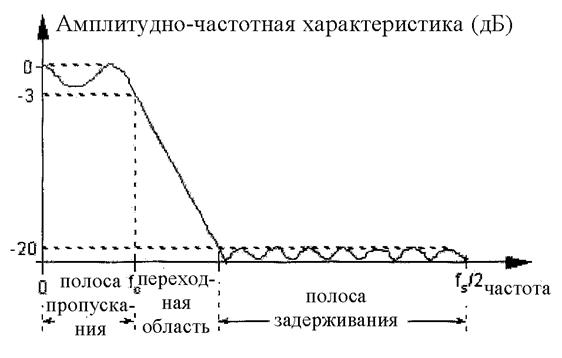
Рис. 7.  Частотный отклик цифрового фильтра нижних частот. Амплитуда, соответствующая полосе задерживания,  равна -20 дБ.

Ширина полосы пропускания (Bandwidth) –будем определять ширину полосы пропускания как ширину полосы частот пропускания фильтра. Для фильтра нижних частот - ширина полосы пропускания равна частоте среза (cutoff frequency). Для полосового фильтра - ширина полосы пропускания обычно определяется как разница частот между верхней и нижней точками полосы  при спаде на 3ДБ.

Эллиптическая функция (Elliptic Function) – математическая функция, используемая для получения самого крутого  спада для определенного порядка  фильтра (filter taps). Однако, у фильтров, спроектированных с помощью эллиптической функции, также называемых фильтры Кауэра (Cauer filter), самая низкая линейность фазовой характеристики по сравнению с остальными  БИХ - фильтрами.  У  эллиптических фильтров  имеются пульсации в полосе пропускания и полосе задерживания.