МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ АГЕНТСТВО ПО ОБРАЗОВАНИЮ
ГОСУДАРСТВЕННОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО
ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ
НОВОСИБИРСКИЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ
ФАКУЛЬТЕТ АВТОМАТИКИ И ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ
КАФЕДРА ВЫЧИСЛИТЕЛЬНОЙ ТЕХНИКИ
Лабораторная работа №1
по дисциплине
«Интеллектуальные системы»
Сравнительный анализ объектов и факторных эффектов
|
Группа: |
АПМ-09 |
|
Выполнил студент: |
Дядичкин Р.В. |
|
Преподаватель: |
Швайкова И.Н. |
Новосибирск, 2009
Содержание. 2
Цель работы. 3
Задание. 3
Ход работы. 4
Импорт данных. 4
Вычисление описательных статистик. 4
Критерии нормальности. 8
Проверка гипотез о равенстве средних для нормальных распределений (t-критерий) 9
Непараметрическая статистика и подгонка распределения. 10
Критерий знаков. 10
Критерий Вилкоксона. 11
Выводы. 13
Познакомиться и приобрести опыт решения задачи сравнения объектов и факторных эффектов по результатам наблюдений методами математической статистики и средствами визуализации данных.
Познакомиться на тестовых примерах использования специализированного пакета статистического анализа с постановкой и способами решения основных задач сравнения объектов, анализа факторных эффектов и создания регрессионных моделей по экспериментальным данным. Необходимо проанализировать предложенные (или самостоятельно выбранные) данные и дать результатам анализа содержательную интерпретацию.
В результате импорта данных из Excel-файла в формат файла Statistica была сформирована таблица, показывающая распределение средней температуры в Барнауле за 2001-2002 год. (см. Workspace таблица «2001-2002 год»).
С среде Statistica были вычислены описательные статистики для каждого месяца наблюдения. Результаты представлены в табл.1
Таблица 1 Числовые статистические характеристики
|
Среднее |
Медиана |
Минимум |
Максимум |
Станд.отклонение |
Симметрия |
Эксцесс |
|
|
1 |
-18,0223 |
-15,3200 |
-42,9100 |
-3,99000 |
10,49711 |
-1,07185 |
0,452883 |
|
2 |
-13,4686 |
-11,3350 |
-31,9600 |
-1,88000 |
9,250295 |
-0,592854 |
-0,747085 |
|
3 |
-3,21161 |
-0,200000 |
-20,5800 |
6,410000 |
7,518214 |
-0,845797 |
-0,117776 |
|
4 |
3,395667 |
2,650000 |
-7,77000 |
12,57000 |
5,206322 |
-0,132979 |
-0,366790 |
|
5 |
16,68452 |
18,36000 |
4,050000 |
25,23000 |
5,933591 |
-0,476972 |
-0,808535 |
|
6 |
18,50433 |
18,72000 |
12,60000 |
23,77000 |
2,877416 |
-0,167668 |
-0,743246 |
|
7 |
17,70161 |
16,78000 |
13,30000 |
23,55000 |
2,844982 |
0,597658 |
-0,648977 |
|
8 |
18,67323 |
18,21000 |
14,39000 |
25,09000 |
2,475455 |
0,809293 |
0,730573 |
|
9 |
11,07433 |
12,09500 |
2,950000 |
18,00000 |
3,888692 |
-0,197623 |
-0,654679 |
|
10 |
2,784516 |
2,510000 |
-6,78000 |
13,26000 |
5,324848 |
0,045851 |
-0,306622 |
|
11 |
-1,01414 |
0,160000 |
-20,2600 |
8,900000 |
7,749019 |
-1,06330 |
0,730834 |
|
12 |
-15,7677 |
-14,9700 |
-36,0800 |
-3,13000 |
8,893879 |
-0,475966 |
-0,317700 |
|
13 |
-6,17710 |
-6,53000 |
-17,3300 |
1,730000 |
4,669076 |
-0,183946 |
0,155767 |
|
14 |
-6,61036 |
-6,00500 |
-20,1200 |
2,130000 |
5,079658 |
-0,610020 |
0,553176 |
|
15 |
-0,547742 |
-0,430000 |
-7,47000 |
3,820000 |
3,210110 |
-0,609981 |
-0,555923 |
|
16 |
2,749667 |
3,670000 |
-11,8300 |
13,18000 |
6,564097 |
-0,615171 |
-0,201869 |
|
17 |
14,35516 |
14,61000 |
4,230000 |
23,72000 |
4,743069 |
-0,177180 |
-0,381384 |
|
18 |
17,70400 |
18,40000 |
11,55000 |
21,26000 |
2,574312 |
-0,633736 |
-0,488532 |
|
19 |
18,33226 |
18,12000 |
14,44000 |
26,59000 |
2,497237 |
1,252880 |
2,759233 |
|
20 |
17,80032 |
18,40000 |
11,60000 |
27,75000 |
4,299410 |
0,314952 |
-0,424198 |
|
21 |
12,80100 |
13,79000 |
2,920000 |
20,54000 |
4,685878 |
-0,281231 |
-0,596066 |
|
22 |
1,956774 |
3,150000 |
-9,00000 |
10,15000 |
4,801101 |
-0,240884 |
-0,743195 |
|
23 |
-2,76533 |
-2,55000 |
-15,1800 |
4,580000 |
4,658720 |
-0,636424 |
0,617802 |
|
24 |
-18,6029 |
-18,8900 |
-29,7800 |
-3,24000 |
6,994123 |
0,218094 |
-0,609189 |
Из анализа таблицы можно сделать некоторые выводы о законах распределения средних температур. Например, анализируя такую статистику, как «эксцесс» можно определить месяца, соответствующие нормальному закону, так как эксцесс нормального распределения равен 0. В данном случае для преобладающего количества месяцев сложно говорить о нормальности законов распределения. В качестве верхней границы для принятия гипотезы о нормальности закона возьмем значение модуля этой статистики «эксцесс» равное 0,5. То же самое можно сказать и про статистику «симметрия» - нормальный закон абсолютно симметричен. В данном случае, можно говорить о смещённости центров масс распределений исследуемых величин. Можно выделить 2 месяца: ноябрь 2001 года и июль 2002 года, как месяцы, в которых числовые статистические характеристики более всего указывают на ненормальность законов распределения средних температур в Барнауле в эти месяцы. Месяца с предположительно нормальным законов распределения помечены в таблицы зеленым цветом.
Также для каждого месяца были построены гистограммы, с наложенной на них нормальной кривой (рис.1-24)
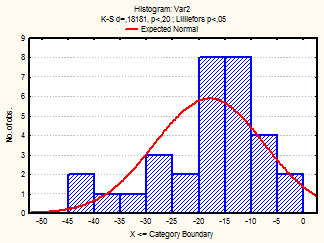
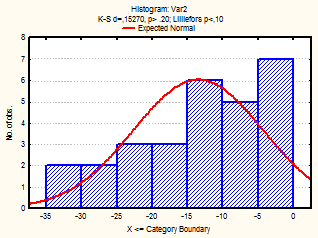
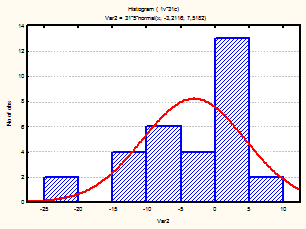
Рис. 1-3 Гистограмма (январь-март 2001г.)
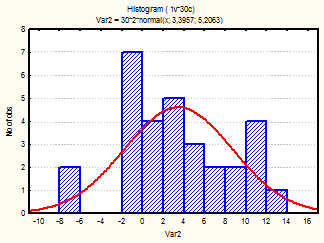
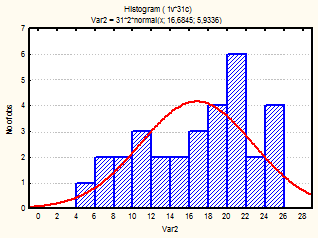
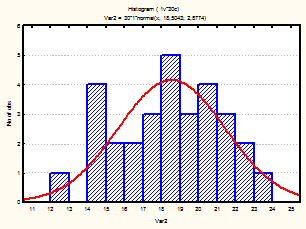
Рис. 3-6 Гистограмма (апрель-июнь 2001г.)
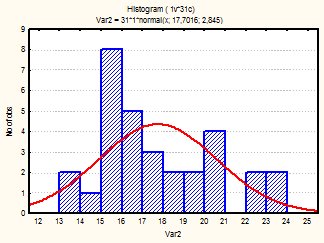
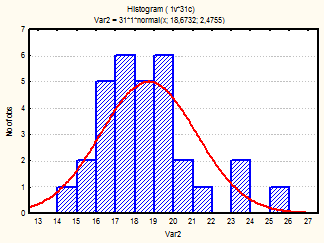
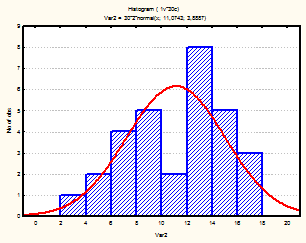
Рис. 7-9 Гистограмма (июль-сентябрь 2001г.)
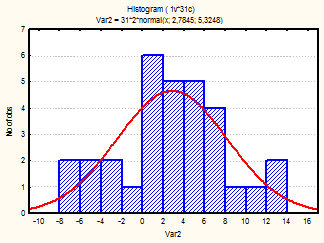
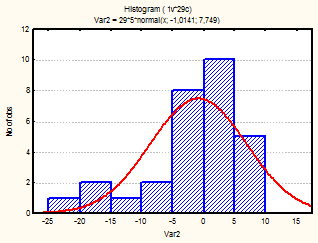
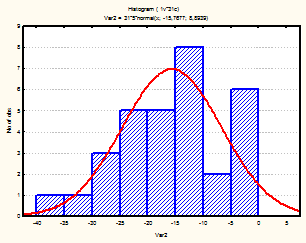
Рис. 10-12 Гистограмма (октябрь-декабрь 2001г.)
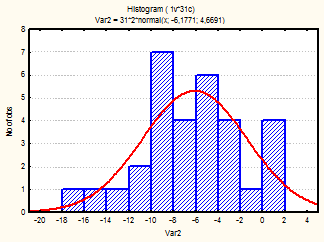
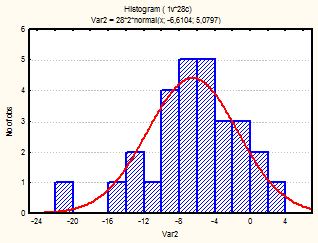
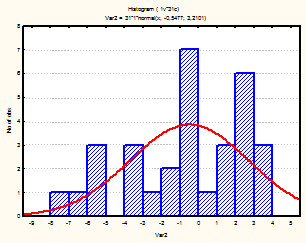
Рис. 13-15 Гистограмма (январь-март 2002г.)
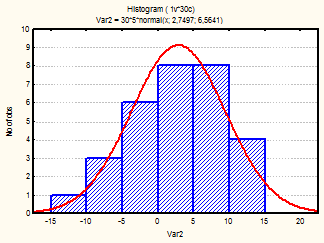
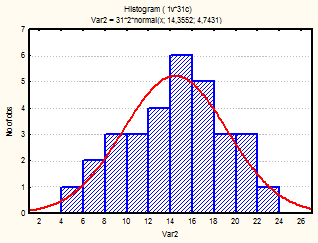
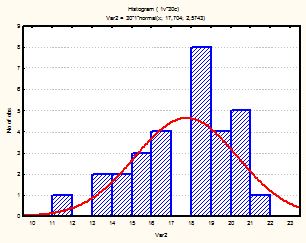
Рис. 16-18 Гистограмма (апрель-июнь 2002г.)
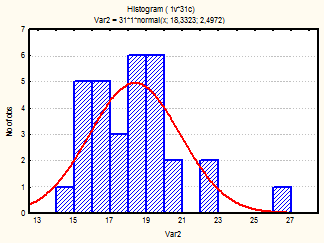
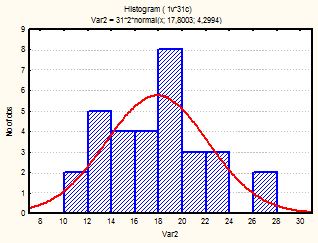
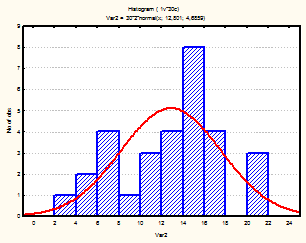
Рис. 19-21 Гистограмма (июль-сентябрь 2002г.)
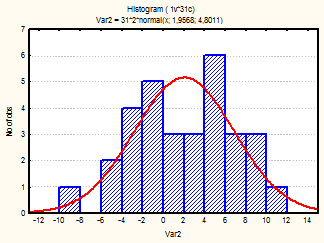
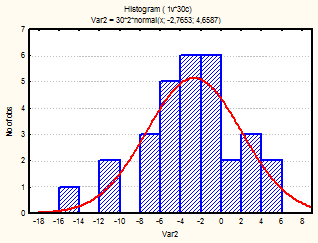
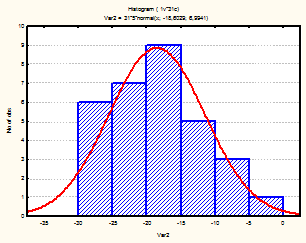
Рис. 22-24 Гистограмма (октябрь-декабрь 2002г.)
Из визуального анализа гистограмм также можно сделать вывода относительно нормальности законов распределения средней температуры по месяцам. Для некоторых месяцев можно увидеть, что распределение бимодально (имеет 2 пика), это может быть связано с влияние целого комплекса факторов на такой показатель, как температура (например, влажность воздуха, скорость и направление ветра и т.д.).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.