Информатика и выч. техника \ Теория и обработка сигналов

Случайные сигналы и их характеристики. Изучение основных характеристик стационарных случайных сигналов, страница 2

С помощь следующего script-файла сгенерируем случайный сигнал X длительностью 1000 отсчётов, подадим его на вход системы с уравнением  и построим диаграммы рассеяния.

N = 1000;

X = randn(1,N);

n=3:1000;

Y(n)=0.8*X(n)+X(n-1)+0.4*X(n-2);

i=1:900;

Y0(i)=Y(i);

Y1(i)=Y(i+1);

subplot(2,2,1);

plot(Y0,Y1,'.');

set(gca,'FontName', 'Times New Roman Cyr', 'FontSize', 10)

title('График рассеяния Yi,Yi+1');

Y0(i)=Y(i);

Y1(i)=Y(i+2);

subplot(2,2,2);

plot(Y0,Y1,'.');

set(gca,'FontName', 'Times New Roman Cyr', 'FontSize', 10)

title('График рассеяния Yi,Yi+2');

Y0(i)=Y(i);

Y1(i)=Y(i+3);

subplot(2,2,3);

plot(Y0,Y1,'.');

set(gca,'FontName', 'Times New Roman Cyr', 'FontSize', 10)

title('График рассеяния Yi,Yi+3');

Y0(i)=Y(i);

Y1(i)=Y(i+4);

subplot(2,2,4);

plot(Y0,Y1,'.');

set(gca,'FontName', 'Times New Roman Cyr', 'FontSize', 10)

title('График рассеяния Yi,Yi+4');

Полученные диаграммы рассеяния изображены на рис. 8.

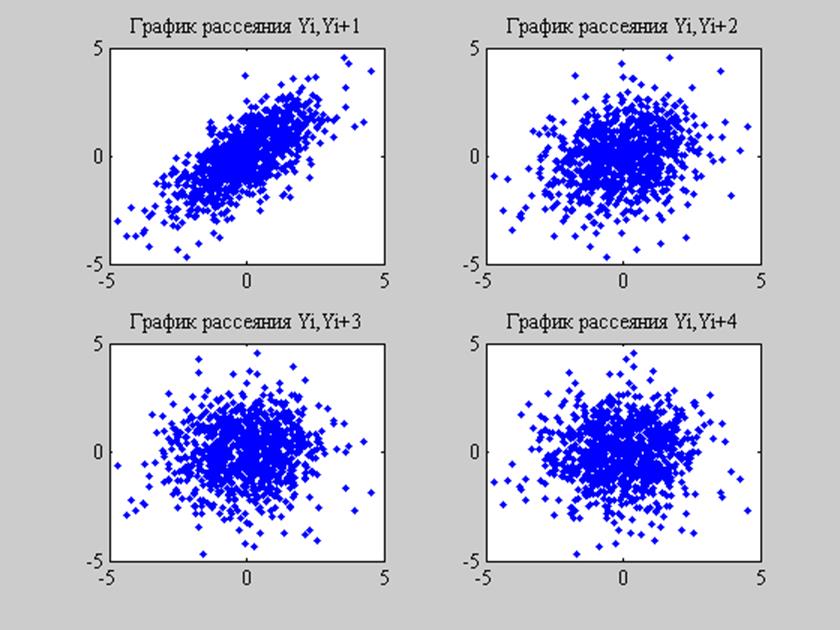
Рис. 8. Диаграммы рассеяния выходного сигнала Y системы.

Диаграммы рассеяния визуализируют зависимость между значениями сигнала Y, разделенными между собой интервалами 1, 2, 3 и 4 отсчёта. Если два значения сильно связаны, то множество точек принимает определенную форму. Если же переменные не связаны, то точки образуют "облако".

Видим, что при сдвиге на 1 отсчёт значения коррелированны больше всего, т.к. диаграмма имеет диагональный характер. На остальных диаграммах корреляция значений меньше и снижается при увеличении интервала между значениями.

5.  Определение оценки АКФ и ВКФ с помощью функции xcorr().

C помощью следующей последовательности команд определим оценку АКФ выходного сигнала системы при подаче на вход случайного сигнала X, используя функцию xcorr().

% выходной сигнал

y = filter([1 0.5 3], [1   0   0], X);

[Kyy1, lags] = xcorr(y, 'biased');

subplot(2,1,1);

stem(lags, Kyy1);

set(gca,'FontName', 'Times New Roman Cyr', 'FontSize', 10)

title('Оценка АКФ xcorr(y) выходного сигнала y');

subplot(2,1,2);

stem(-(N+3):(N+3), Kyy)

set(gca,'FontName', 'Times New Roman Cyr', 'FontSize', 10)

title('АКФ выходного сигнала по (6)');

xlabel('m');

Получим:

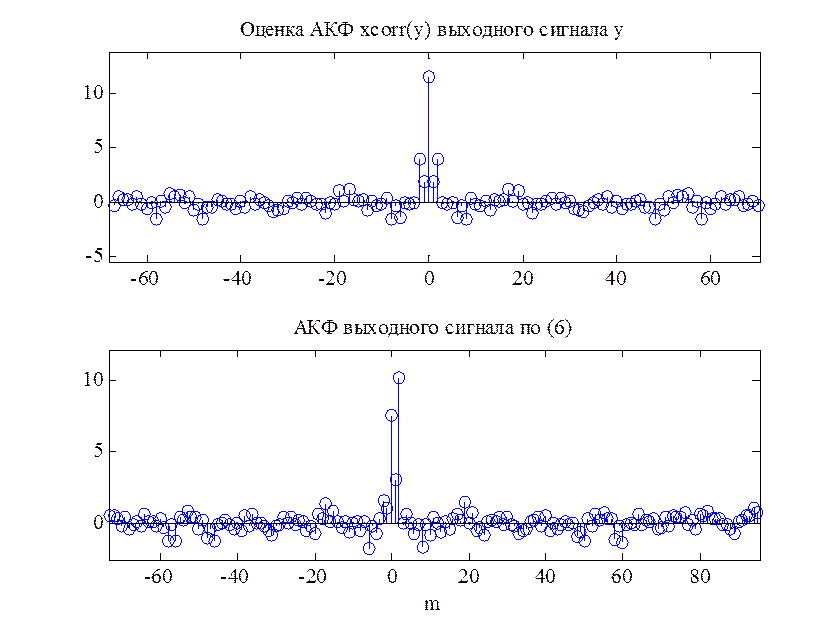
Рис. 9. График оценки АКФ сигнала X.

Видим, что график АКФ, найденной по значениям выходного сигнала фильтра, совпадает с графиком АКФ, определённой по выражению (6). Значит, АКФ выходного сигнала системы может быть определена как свёртка импульсной характеристики данной системы с АКФ входного сигнала.

Взаимная корреляционная функция (ВКФ) является функцией корреляции между двумя случайными процессами X и Y, т.е. характеризует степень зависимости этих сигналов, их согласованность.

C помощью следующей последовательности команд определим ВКФ выходного и входного сигналов системы.

[Kxy, lags] = xcorr(X, y, 'biased');

stem(lags, Kxy);

set(gca,'FontName', 'Times New Roman Cyr', 'FontSize', 10)

title('ВКФ входного и выходного сигналов');
 

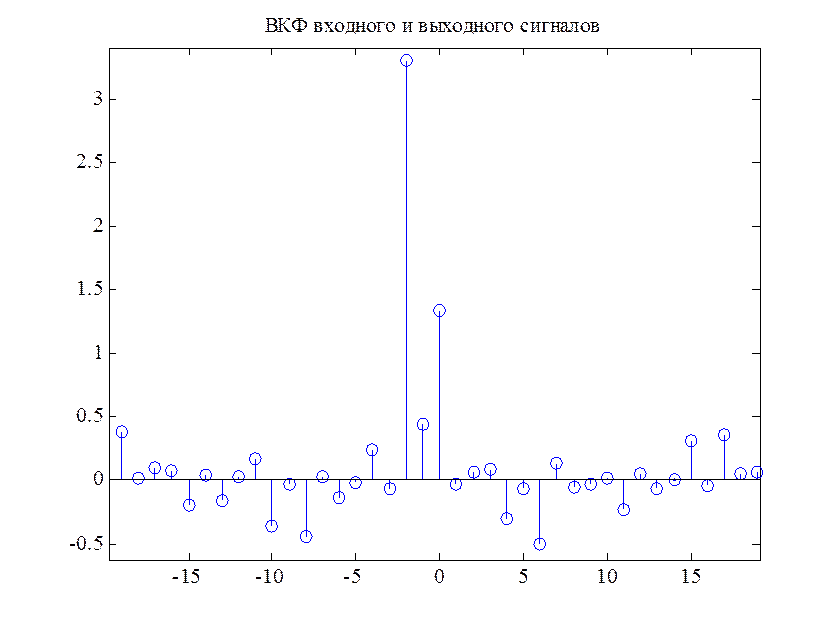
Рис. 10. ВКФ выходного и входного сигналов системы.

Судя по графику ВКФ сигналов X и Y (рис. 10) можно сделать вывод об их зависимости, что ожидаемо, т.к. сигнал Y является отфильтрованным сигналом X (выходным сигналом заданной системы).

6.  Определение АЧХ фильтра, спектральной плотности мощности его входного и выходного сигналов.

Основной характеристикой случайного сигнала в частотной области является его спектральная плотность мощности, которая выражает распределение средней мощности сигнала по частоте.

Спектр мощности может быть оценён по выражению

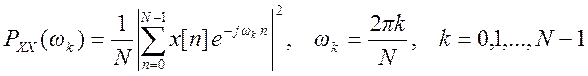                                      (8)

Определим спектр мощности входного и выходного сигнала системы с уравнением

Определим АЧХ заданного фильтра.

Z – преобразование от уравнения:

Передаточная функция фильтра имеет вид

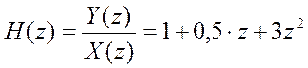
Частотную характеристику фильтра можно определить, сделав замену  в выражении передаточной функции.

Получим частотную характеристику вида

                                                                                   (9)

С помощью следующего script-файла сгенерируем гауссовский случайный сигнал X длительностью 1000 отсчётов, подадим его на вход фильтра с ЧХ (9) и построим графики АЧХ фильтра и спектральной плотности мощности входного и выходного сигналов. Для вычисления спектра мощности будем использовать функцию

[S, f] = psd(x, nfft, Fs).

Ts=0.01; T=10;  % интервал отсчетов и длительность сигнала

df=1/T; Fmax=1/Ts;

f=0:df:Fmax/2;  % частотная шкала

d1=length(f);

% Частотная характеристика фильтра

H=1./(1+0.7*exp(-j*2*pi*f*Ts)+0.9*exp(-j*4*pi*f*Ts));%5+2*exp(-j*2*pi*f*Ts)-exp(-j*4*pi*f*Ts);

figure(1)

subplot(3,1,1), plot(f,abs(H))

title('АЧХ Фильтра')

% Вычисление и построение спектра мощности входного шума

t=0:Ts:T;

X=randn(1, length(t));  % Генерирование входного шума

[Sxx, f1]=psd(X,d1, Fmax); % Вычисление спектра мощности входа

subplot(3,1,2), stem(f1,Sxx)

title('Спектр мощности входа')

% Вычисление и построение спектра мощности выхода

i=2:length(X);

Y=zeros(1, length(X));

% Формирование выходного сигнала фильтра

b=1; a=[1,0.7,0.9];

Y=filter(b,a,X);

[Syy, f2]=psd(Y,d1,Fmax); % Спектр мощности выхода

subplot(3,1,3), stem(f2,Syy)

title('Спектр мощности выхода')

xlabel(' Частота,  Гц')

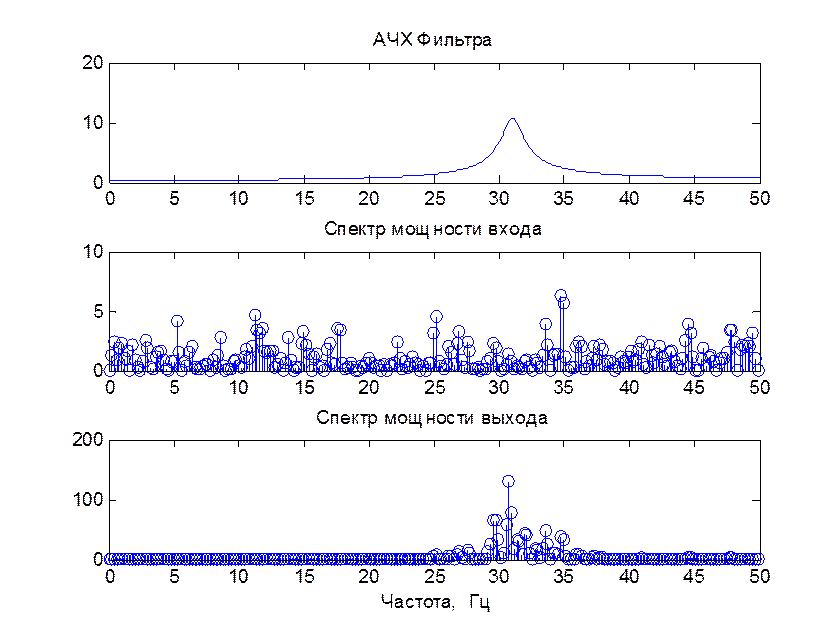
Рис. 11. АЧХ фильтра и спектральная плотность

мощности входного и выходного сигналов.

По виду АЧХ использованного фильтра определяем, что это полосовой фильтр.

Случайный сигнал, подаваемый на вход фильтра, имеет спектральные составляющие на всех рассмотренных частотах. На графике спектра мощности выходного сигнала видим, что частоты не входящие в полосу пропускания фильтра были подавлены в процессе фильтрации, а входящие в полосу пропускания остались без изменения, т.е. полученный вид выходного сигнала соответствует АЧХ фильтра.  

Выводы:

1.  Случайным называется сигнал, который в любой момент времени представляет собой случайную величину и может быть описан только вероятностными законами и характеристиками.

2.  Одними из важнейших характеристик случайных сигналов являются математическое ожидание и дисперсия. Математическим ожиданием называется среднее значение случайной величины, а дисперсия характеризует рассеяние сигнала относительно его среднего значения. В п. 1 было показано, что данные характеристики могут быть оценены по одной реализации случайного сигнала длиной N (выражения (1) и (2)).

3.  Ещё одной характеристикой случайных сигналов является АКФ, которая определяет степень зависимости отсчетов сигнала, разделенных друг от друга интервалом m. АКФ может быть оценена по выражению (7) или с помощью функции xcorr() Matlab. В п. 3 было показано, что оценка АКФ близка к истинному значению (рис. 3, 5).

4.  АКФ выходного сигнала системы можно определить, зная импульсную характеристику системы и АКФ входного сигнала (выражение (6)). В п. 5 было показано, что прямое вычисление АКФ отфильтрованного сигнала и определение её по выражению (6) дают одинаковые результаты.

5.  При подаче на вход системы некоррелированного сигнала на выходе получается сигнал, отсчёты которого зависят друг от друга (п. 3 рис. 7).

6.  Основной характеристикой случайного сигнала в частотной области является его спектральная плотность мощности, которая выражает распределение средней мощности сигнала по частоте.

Скачать файл