Министерство Образования и Науки Российской Федерации
Новосибирский Государственный Технический Университет
Отчет по лабораторной работе № 1
по курсу "Теория информационных процессов и систем"
Работа в командном окне системы MatLab
Факультет: АВТФ Преподаватель: проф. Рабинович Е.В.
Группа: АТ-73
Студент: Пархомук Д.В.
г. Новосибирск
2010 г
Целью данной лабораторной работы является ознакомление с основами работы в среде MatLAB: изучение типов используемых данных, работа с массивами, построение графиков и т.д.
Задание 1
Нахождение точек пересечения двух кривых: y = x2 – 5x + 3 и y = 7x – 4.
Листинг m-файла p1.m
x=-10:15;
y1=x.^2-5*x+3;
y2=7*x-4;
plot(x,y1,'r',x,y2,'g')
title('Задание 1. График пересечения кривых y1 и y2')
legend('y1=x^2-5x+3','y2=7x-4')
xlabel('x')
ylabel('y')
grid
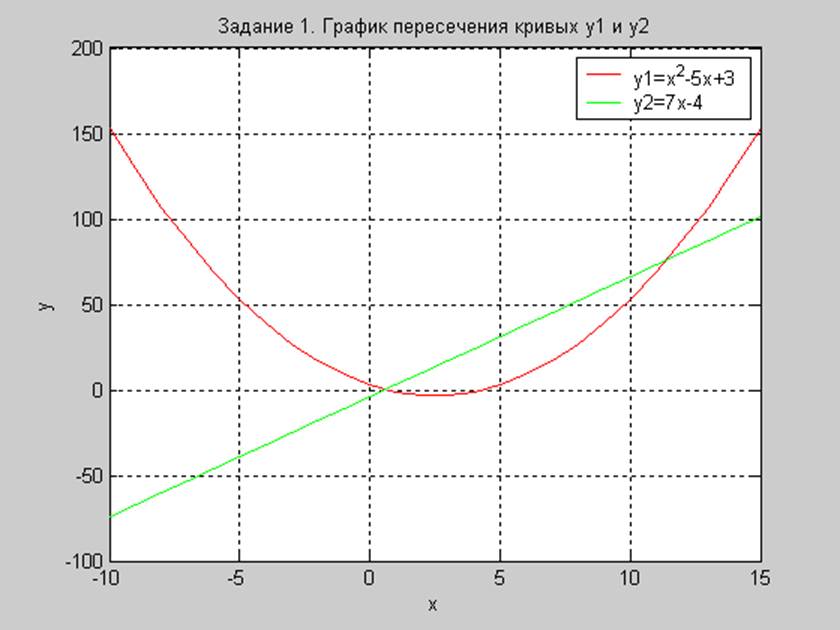
Рис. 1.1. Графическое решение задания 1 - нахождение пересечения двух кривых
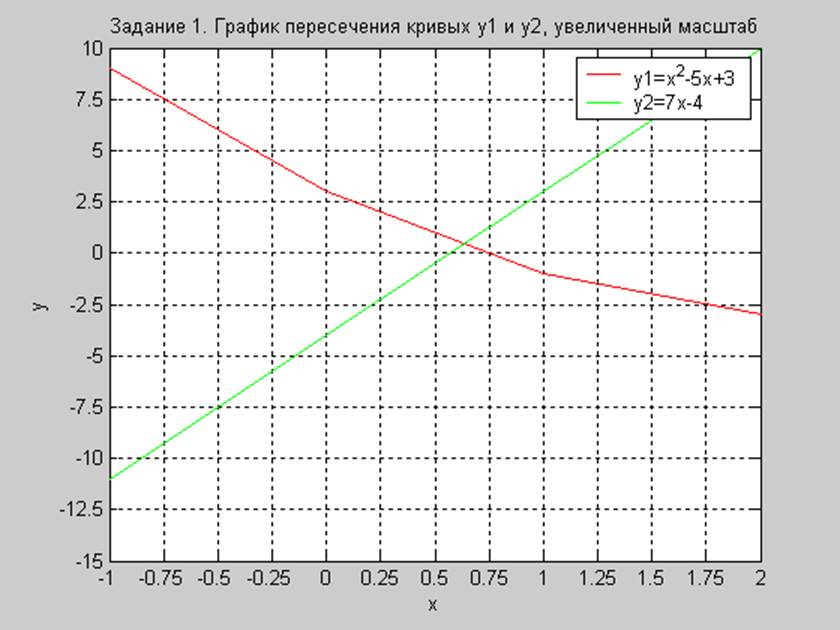
Рис. 1.2. Координаты первой точки пересечения, увеличенный масштаб.
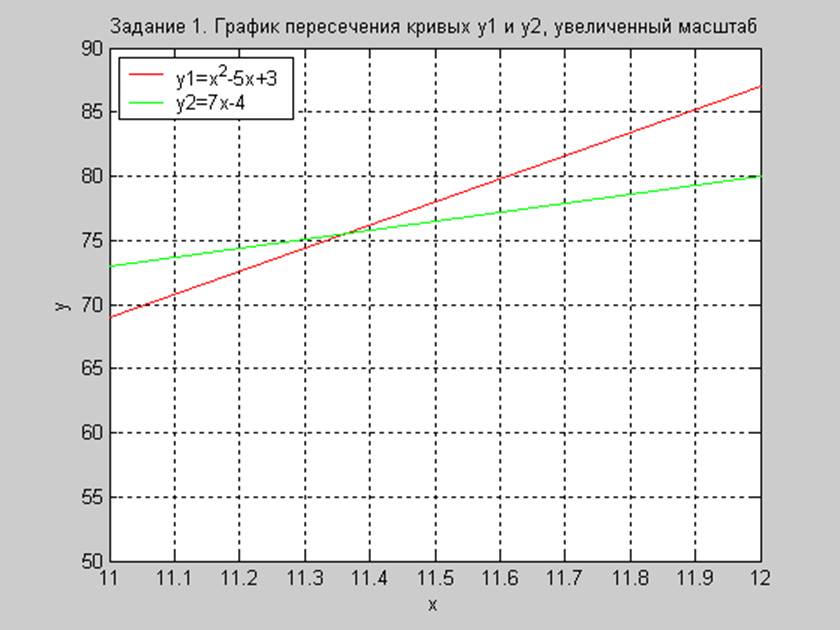
Рис. 1.3. Координаты второй точки пересечения, увеличенный масштаб.
Из графиков можно увидеть, что кривые y = x2 – 5x + 3 и y = 7x – 4 пересекаются в двух точках с координатами (0.6; 0.5) и (11.35; 76.0)
Решение с помощью функции fsolve():
x1=fsolve('x.^2-5*x+3-7*x+4',0,optimset('Display','off'))
y1=7*x1-4
x2=fsolve('x.^2-5*x+3-7*x+4',10,optimset('Display','off'))
y2=7*x2-4
Результат вычислений:
x1 = 0.6148
y1 = 0.3038
x2 = 11.3852
y2 = 75.6962
Задание 2
Нахождение точки экстремума функции y = (x+2)(x-4)
Листинг m-файла p2.m
subplot(211)
x=-3:0.5:5;
y=(x+2).*(x-4);
plot(x,y);
xlabel('x'),ylabel('y'),grid
title('График функции y=(x+2)(x+4)')
x1=-10:10;
y1=diff((x1+2).*(x1-4));
subplot(212)
plot(-9:10,y1)
title('График производной функции y=(x+2)(x+4)')
xlabel('x'),ylabel('y'),grid
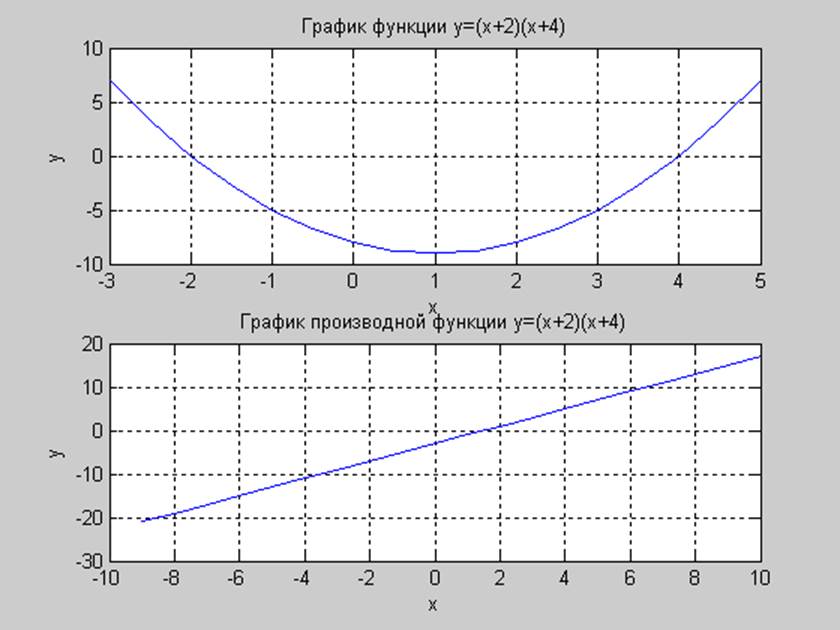
Рис. 2. Нахождение экстремума функции
Решение с помощью функции diff():
syms x y dif
y=(x+2).*(x-4)
dif=diff(y)
x0=fzero(inline(dif),1)
y0=(x0+2)*(x0-4)
Результат вычислений:
Производная функции y = (x+2)(x-4):
dif = 2*x-2
Координаты экстремума функции:
x0 = 1
y0 = -9
>>
Функция y=(x+2)(x-4) имеет минимум при x=1. Минимальное значение функции равно -9.
Задание 3
Дан треугольник ABC: A(-1;-2), B(-1;4), C(5;4). Найти координаты основания перпендикуляра, опущенного из точки B на сторону AC.
Листинг m-файла p3.m
syms X AC BD;
x_a = -1;
y_a = -2;
x_b = -1;
y_b = 4;
x_c = 5;
y_c = 4;
% построение треугольника АВС
x=[x_a x_b x_c x_a]
y=[y_a y_b y_c y_a]
plot (x,y)
hold on
k = (y_c-y_a)/(x_c-x_a) % коэффициент наклона прямой АС
AC = y_a + k*(X-x_a) % уравнение прямой АС (y-y0=k(x-x0))
BD = y_b - (1/k)*(X-x_b) % уравнение прямой, перпендикулярной АС и
проходящей через точку В.
x0 = fsolve(inline(AC-BD) ,1,optimset('Display','off'))
y0 = y_a + k*(x0-x_a)
plot([x_b x0], [y_b y0], 'r')% построение высоты
hold on
plot(x0, y0,'g+')
%обозначение вершин
set(gca,'FontName','Arial','FontSize',10);
text (x0+0.2,y0,'D');
text (x_a,y_a-0.2,'A');
text (x_b,y_b+0.2,'B');
text (x_c,y_c+0.2,'C');
axis ([-3 6 -3 6]);
xlabel('Ось X');
ylabel('Ось Y');
Title('Задание 3. Нахождение координат основания высоты треугольника')
grid on
legend('Треугольник АВС','Высота BD','Основание высоты',4);
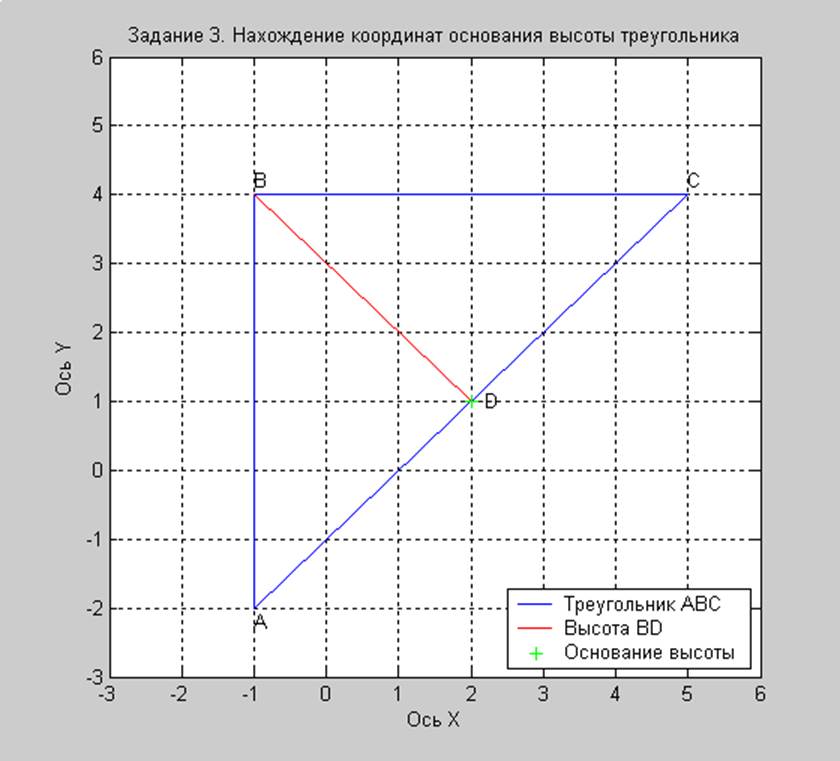
Рис. 3. Нахождение координат основания высоты BD треугольника ABC
Результат вычислений:
Угловой коэффициент прямой АС:
k = 1
Уравнение прямой АС:
AC = -1+X
Уравнение прямой BD:
BD = 3-X
Координаты основания высоты (точка D):
x0 = 2
y0 = 1
Задание 4
Нахождение основания перпендикуляра, опущенного из точки A(3;10) на окружность радиуса 4, с центром в начале координат.
Листинг m-файла p4.m
x1=0;
y1=0;
x2=3;
y2=0;
x3=3;
y3=10;
% нахождение координат основания перпендикуляра (x4; y4)
r12=sqrt(((x1-x2)^2)+((y1-y2)^2));
r23=sqrt(((x2-x3)^2)+((y2-y3)^2));
r13=sqrt(r12^2+r23^2);
r14=4;
x4=r14*r12/r13
y4=r14*r23/r13
%построение графика окружности
x=-4:0.1:4;
y=sqrt(16-x.*x);
plot(x,y)
hold on
y=-sqrt(16-x.*x);
plot(x,y)
plot(x3,y3,'xg') %точка (3;10)
x=[x1 x3];
y=[y1 y3];
plot(x,y,'r') % построение прямой
plot(x4,y4,'dc') % искомая точка
x=[x3 x2 x1];
y=[y3 y2 y1];
plot(x,y,'k')
x=[x4 x4 x1];
y=[y4 y1 y1];
plot(x,y,'k');
% оформление
axis([-4 11 -4 11])
title('Задание 4. Нахождение основания перпендикуляра');
xlabel('Ось x'); ylabel('Ось y');
legend('Окружность', 'радиуса 4','Точка A(3;10)', 'Перпендикуляр', 'Точка касания');
grid
text (x1-1,y1-0.5,'(0; 0)');
text (x2-1,y2-0.5,'(3; 0)');
text (x3,y3+0.5,'(3; 10)');
text (x4-1.5,y4+0.5,'(x; y)');
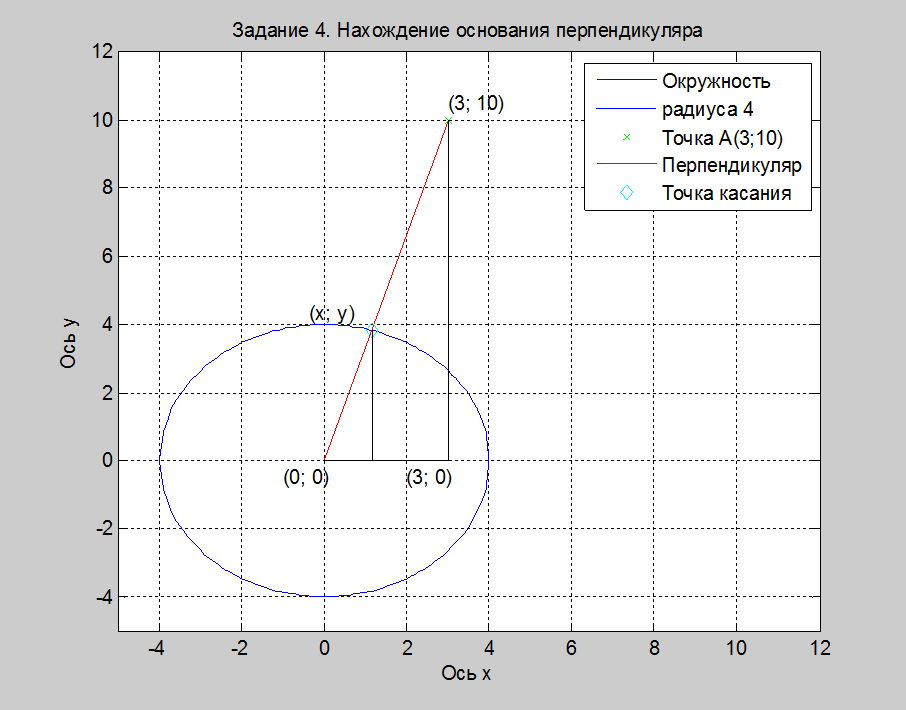
Рис. 4. Нахождение основания перпендикуляра, опущенного из точки А(3;10)
на окружность радиуса 4 с центром в начале координат.
Результаты вычислений: координаты основания перпендикуляра:
x4 = 1.1494
y4 = 3.8313
Задание 5
На графике функции y = (5+x)(5-x) определить точки, касательная в которых имеет угол наклона.
Листинг m-файла p5.m
alpha=input('Vvedite ugol naklona : ');
if (alpha==90)
k='Error! Print another angle!'
else
k=tan(alpha*pi/180);
syms x y yd
y=(5+x).*(5-x);
yd=diff(y)
x0=fzero(inline(yd-k),1)
y0=(5+x0)*(5-x0)
x_p=-10:0.1:10;
y_p=(5-x_p).*(5+x_p);
plot(x_p,y_p);
hold on
a=-10:0.1:10;
b=k*(a-x0)+y0;
plot(a,b,'r')
plot(x0,y0, 'xg')
xlabel('Ось X');
ylabel('Ось Y');
Title('Задание 5. Нахождение точки, где касательная имеет угол наклона')
grid on
axis([-10 10 0 35])
legend('Заданная функция','Касательная','Точка касания',2);
end
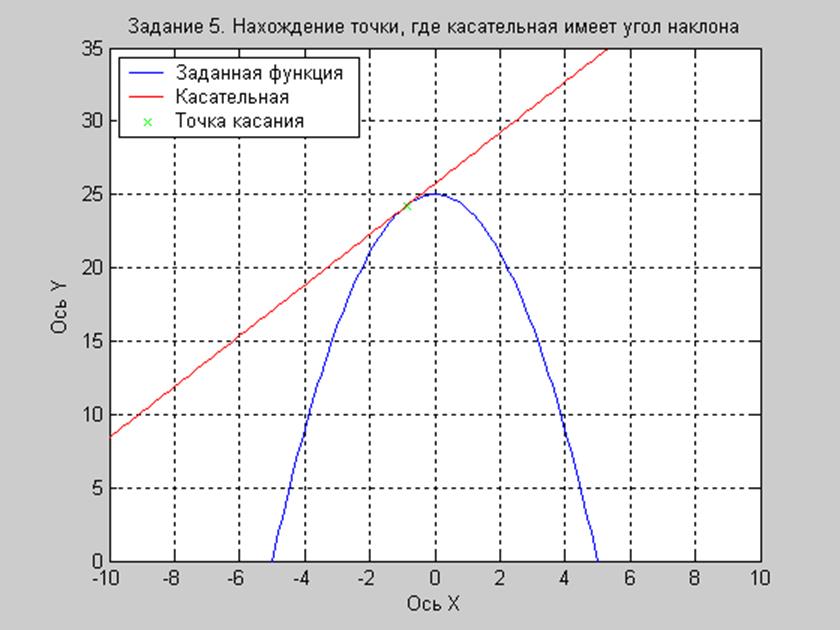
Рис. 5. Касательная к графику функции y = (5+x)(5-x), имеющая угол наклона 60°
Результаты:
>>Vvedite ugol naklona : 60
Точка касания:
x0 = -0.8660
y0 = 24.2500
Касательная в точке (-0.8660, 24.2500) имеет требуемый угол наклона 60°
Так как данная функция непрерывна и имеет производную во всех точках, то возможно провести касательную в любой ее точке, поскольку тангенс угла наклона определен на всей числовой оси.
Выводы:
В ходе выполнения данной лабораторной работы я ознакомился с системой MatLab и некоторыми ее возможностями, а именно:
· Ознакомление с командным окном системы MatLab
· Построение графиков и их оформление (отображений осей, легенды, подписей).
· Решение уравнений (графически и при помощи специальных функций)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.